Пространство и время

§ 5.1. Пространство и время в естествознании

Эволюция взглядов на пространство и время

Пространство и время - фундаментальные категории современного естествознания. Физические, биологические, географические и другие величины непосредственно или опосредованно связаны с пространственно-временными характеристиками объектов. Ученые ведут дискуссии о сущности пространства и времени, об их основных свойствах. Проблемы пространства и времени во многом решаются в рамках господствующей в данную эпоху парадигмы. Картинам мира разных исторических эпох с присущими им культурами соответствовали свои пространственно-временные представления. Более того, выбор самих моделей пространства и времени зависит от конкретных целей и масштабов, в которых существует изучаемое явление или объект.

Нашим далеким предкам мир представлялся маленьким и кратковременным; для них пространство замыкалось видимыми очертаниями моря и гор [1]. Пространство первобытных людей было очень неоднородным. На территории племени выделялись тотемные центры - места, где пространство, по мнению членов племени, обладало максимально благоприятными качествами. Место обитания племени было также благотворным пространством, ибо здесь похоронены предки, охраняющие племя. За относительно упорядоченным пространством племенной территории располагалось внешнее пространство, наделенное отрицательными качествами. Развитие межплеменных связей обусловило появление представлений о множественности оазисов упорядоченного бытия. Постепенно мифологический мир приобретает многоуровневый характер: верхний уровень предков или иных сакральных персонажей, средний уровень людей и нижний уровень мертвых. Подобные уровни объединяются с помощью «мирового древа», креста и т.п.

Что касается восприятия времени, то первобытное мышление не ощущало как однородные следующие друг за другом отрезки времени и приписывало некоторым периодам дня и ночи, лунного месяца, года и т.д. свойство оказывать благоприятное или гибельное влияние. В более развитой мифологии каждому уровню мира присуще свое время, отличающееся такими параметрами, как ритм, длительность и т.п. Для мифологического времени характерна ориентация на прошлое. Мифологический прамир помещается в то время, когда еще не было времени, оно само еще созидалось. Более того, мифологическое время, соотнесенное с прошлым, оказывается вместе с тем настоящим и даже будущим, так как первобытные представления порождены циклическим видением времени. Колесо времени двигалось из прошлого, захватывало настоящее и через будущее уносило их в прошлое. Прошлое претерпевало изменения, аккумулируя достижения первобытного мышления и познания.

Древним грекам мир не представлялся столь маленьким [1]. Они были смелыми мореплавателями; установили торговые и культурные связи со многими народами, населявшими берега Средиземного моря. Древнегреческому ученому Эратосфену удалось определить длину земной окружности. В античной натурфилософии на смену опоясывающему Землю Океану приходит линейно упорядоченная река времени, которая катит свои воды из прошлого через настоящее в будущее, унося нас из детства в старость. (Эту линейную модель восприняло христианство, где присутствуют три момента времени: сотворение мира, распятие Христа и загробный мир — конечный пункт. Однако в христианстве река времени потекла вспять: настоящее непрерывно переходит из будущего в прошлое. Здесь более приемлем образ песочных часов. Бог сотворил время и, отмерив нужное количество, «засыпал» его в верхнее отделение часов - это и есть будущее, которое через отверстие (настоящее) стекает в нижнее отделение - в прошлое.)

В античности существовал широкий спектр представлений о сущности пространства и времени. Представители элейской школы в Древней Греции отрицали возможность существования пустого пространства, или, по их выражению, небытия.

Эмпедокл, поддерживая учение о невозможности пустоты, высказывался в пользу реальности изменения и движения, считая, что пустого пространства не существует, и в качестве доказательства указывал: если рыбы передвигаются в воде, следовательно, все объекты также существуют в определенной среде. Напротив, Демокрит утверждал, что пустота существует и необходима для перемещений и соединений атомов. У древнегреческого математика Евклида пространственные характеристики объектов обрели строгую математическую форму. В это время зарождаются геометрические представления об однородном и бесконечном пространстве, высказываются предположения о шарообразности Земли и о Солнце как центре Вселенной.

В античное время возникает первая целостная система мира - геоцентрическая система К. Птолемея, в которой планеты, Солнце и другие небесные тела обращаются вокруг Земли по орбитам, представляющим сложное сочетание круговых орбит -деферентов и эпициклов. В центр деферента помещалась Земля, и принималось, что планета движется по эпициклу (системе эпициклов), центр которого равномерно перемещается по деференту. Система Птолемея представляла собой универсальную модель мира, где время было бесконечным, а пространство - конечным, в котором происходит равномерное круговое движение небесных тел вокруг неподвижной Земли.

Согласно Библии, Вселенная состоит из круглой плоской Земли, накрытой сверху твердым куполообразным небесным сводом, под которым движутся облака и небесные светила. Все религии сходятся на том, что мир был некогда сотворен, и при этом называют срок 6-9 тыс. лет.

Начиная с XV в. представления о пространстве и времени значительно расширяются. Этому активно способствовали Великие географические открытия, давшие представления о пространстве в пределах Земли и эмпирически доказавшие шарообразность нашей планеты. Изменение научной картины мира произошло с появлением гелиоцентрической системы мира, предложенной Н. Коперником (1543), где Солнце — центральное тело, вокруг которого обращаются планеты. Гелиоцентрическая система мира сменила представление о Земле как центре мироздания. Теория Коперника направила движение естественнонаучной мысли к признанию безграничности и бесконечности пространства. Система мира Коперника унаследовала высказанные ранее, но не воспринятые современниками идеи Аристарха Самосского (III в. до н.э.), который полагал, что звезды и Солнце неподвижны, Земля вращается вокруг Солнца по окружности, расстояние от Земли до звезд бесконечно большое, а также мыслителя раннего Возрождения Николая Кузанского (XV в.), который утверждал, что Земля, как и любое другое тело, не может быть центром Вселенной. Развитие взглядов Николая Кузанского и Коперника получило в теории Дж. Бруно, который связал бесконечность Вселенной и пространства. Бруно писал, что Вселенная должна быть бесконечной благодаря возможности и сообразности бытия бесчисленных миров, подобных нашему.

В начале XVII в. И. Кеплер в гелиоцентрической картине движения планет увидел действие единой физической силы. Он установил универсальную зависимость между периодами обращения планет и средними расстояниями их до Солнца, ввел представление об их эллиптических орбитах.

Огромную роль в развитии представлений о пространстве сыграл сформулированный Г. Галилеем принцип относительности, расширение которого во многом привело к современным научным представлениям о пространстве и времени. Он заметил, что, находясь в помещении под палубой корабля и наблюдая за всем, что там происходит, нельзя определить, покоится корабль или он движется равномерно и прямолинейно. Галилей сделал вывод, что механическое движение относительно, а законы, которые его определяют, абсолютны, т.е. безотносительны. Его взгляды коренным образом отличались от общепринятых в то время представлений Аристотеля о существовании «абсолютного покоя» и «абсолютного движения».

Дальнейшее развитие представлений о пространстве и времени связано с именем Р. Декарта, который полагал, что все явления природы объясняются механическим взаимодействием элементарных материальных частиц. Взаимодействие он представлял в виде давления или удара при соприкосновении частиц друг с другом и ввел, таким образом, в естествознание идею близкодействия. Он поставил знак равенства между материальностью и протяженностью, т.е., отрицая пустое пространство, отождествил пространство с протяженностью.

Новая картина мира была предложена И. Ньютоном. Распространив на всю Вселенную закон тяготения, он пришел к выводу, что Вселенная бесконечна. Лишь в этом случае в ней может находиться множество космических объектов - центров гравитации, связанных между собой силой тяготения. Пространство и время Ньютон характеризует как вместилища самих себя и всего существующего: во времени все располагается в порядке последовательности, в пространстве — в порядке положения. При этом Ньютон различал два типа понятий пространства и времени — абсолютные (истинные, математические) и относительные (кажущиеся, обыденные). Абсолютное время само по себе и без всякого отношения к чему-либо внешнему протекает равномерно и иначе называется длительностью, а абсолютное пространство безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным. Относительное время есть постигаемая чувствами внешняя мера продолжительности, употребляемая в обыденной жизни вместо истинного времени (час, день, месяц, год), а относительное пространство есть мера или какая-либо его ограниченная подвижная часть, которая определяется нашими чувствами по положению его относительно некоторых тел и которая в обыденной жизни принимается за пространство неподвижное. Для своих построений Ньютон использовал модели абсолютного пространства и времени.

Немецкий ученый Г.В. Лейбниц развивал реляционную концепцию пространства и времени, отрицающую существование пространства и времени как абсолютных сущностей. Указывая на чисто относительный (реляционный) характер пространства и времени, Лейбниц считал, что пространство и время есть нечто относительное (пространство - порядок сосуществования, а время — порядок последовательностей) и не могут рассматриваться в отрыве от самих «вещей». Однако идеи Лейбница о пространстве и времени не получили распространение среди его современников.

Ньютоновская концепция пространства и времени и принцип относительности Галилея, на основе которых строилась физическая картина мира, господствовали вплоть до конца XIX в. Принятие абсолютного времени и постулирование абсолютной и универсальной одновременности во всей Вселенной стало основой для теории дальнодействия. В качестве дальнодействующей силы выступало тяготение, которое с бесконечной скоростью, мгновенно и прямолинейно распространялось на бесконечные расстояния. Эти мгновенные, вневременные взаимодействия объектов служили физическим каркасом для обоснования абсолютного пространства, существующего независимо от времени.

Изучение электромагнитных явлений выявило ряд существенных отличий их свойств от механических свойств тел. Если в механике Ньютона силы зависят от расстояний между телами и направлены по прямым, то в электродинамике (теории электромагнитных процессов), созданной в XIX в. английскими физиками М. Фарадеем и Дж.К. Максвеллом, силы зависят от расстояний и скоростей и не направлены по прямым, соединяющим тела, распространение же сил происходит не мгновенно, а с конечной скоростью. Из этого вытекал вывод о конечной скорости распространения электромагнитных взаимодействий и существовании электромагнитных волн. Свет, магнетизм, электричество стали рассматриваться как проявление единого электромагнитного поля. Открытие существования поля в пространстве между зарядами и частицами было значимо для описания свойств пространства и времени. Перенос принципа относительности на электродинамику не представлялся возможным, так как в то время считалось, что все пространство заполнено особой средой - эфиром, натяжения в котором истолковывались как напряженности электрического и магнитного полей. Эфир не влиял на механические движения тел, но на электромагнитных процессах движение относительно эфира («эфирный ветер») должно было сказываться. В частности, предполагалось, что «эфирный ветер» должен влиять на распространение света. Однако попытки обнаружить «эфирный ветер» не увенчались успехом. Так, американский физик А. Майкельсон поставил опыт, который доказывал независимость скорости света от движения Земли. Результаты опыта Майкельсона не поддавались объяснению с помощью понятий классической механики.

Расширение представлений о пространстве и времени связано с распространением принципа относительности Галилея на системы отсчета, которые движутся по отношению друг к другу равномерно и прямолинейно под действием инерции (инерциальные системы отсчета) со скоростями, сопоставимыми со скоростью света с. Для таких систем X. Лоренц предложил преобразования, носящие его имя. При v << с преобразования Лоренца переходят в преобразования Галилея, но если скорость v сопоставима со скоростью света с, то проявляются существенные отличия от нерелятивистской картины пространства-времени:

◊ события, которые происходят одновременно в одной системе отсчета, перестают быть одновременными в другой; меняется и закон преобразования скоростей;

◊ пространственные и временные промежутки не остаются неизменными при переходе из одной системы отсчета в другую, движущуюся относительно первой со скоростью v.

Важный шаг в понимании сущности пространства и времени связан с созданием А.Эйнштейном (1905) специальной теории относительности. Он показал, что в преобразованиях Лоренца отражаются не реальные изменения размеров тел при движении (что можно представить лишь в абсолютном пространстве), а изменения результатов измерения в зависимости от движения системы отсчета. Относительными оказывались и «длина», и «промежуток времени» между событиями, и даже «одновременность» событий, иначе говоря, не только всякое движение, но и пространство, и время. Исходя из невозможности обнаружить абсолютное движение, Эйнштейн сделал вывод о равноправии всех инерциальных систем отсчета. Он сформулировал два постулата, делавших излишней гипотезу о существовании эфира и составивших основу обобщенного принципа относительности: 1) все законы физики одинаково применимы в любой инерциальной системе отсчета и не должны меняться при преобразованиях Лоренца; 2) свет всегда распространяется в свободном пространстве с одной и той же скоростью независимо от движения источника.

В рамках общей теории относительности Эйнштейна считается, что структура пространства-времени определяется распределением масс материи. Так, в классической механике принимается, что если бы вдруг все материальные вещи исчезли, то пространство и время остались бы. Согласно теории относительности, пространство и время исчезли бы вместе с этими вещами.

Пространство и время в различных отраслях естествознания

В современной науке используются такие понятия, как физическое, геологическое, географическое, биологическое, психологическое, социальное пространство и время [4, 11, 12 и др.]. Проиллюстрируем это на двух видах пространства и времени - биологическом и психологическом.

Биологическое пространство и время характеризуют специфические пространственно-временные свойства параметров органической материи: асимметрию расположения атомов в молекулах белка и нуклеиновых кислот; собственные временные ритмы и темпы изменения внутриорганизменных и надорганизменных биосистем; взаимосвязь и синхронизацию ритмов друг с другом, а также с вращением Земли вокруг оси и сменой времен года.

Для анализа биологического времени человека полезно обратиться к рис. 5.1 [2], где дана зависимость темпа биологического времени человека от его физического возраста. График построен на основе анализа данных о длительности заживления ран, температуре тела, составе крови, концентрации ДНК в организме, содержании глюкозы в тканях и показывает, что если для 10-летнего человека принять темп биологического времени за один год, то в трехлетнем возрасте этому времени соответствует 6 лет, а в 70-летнем - всего несколько месяцев. Аналогичные графики построены для рыб, мух дрозофил, мышей, лошадей, моллюсков. Более того, такие графики зависимости темпа времени системы от его возраста можно строить и для неживой природы в виде графика скорости разрушения горных систем разного возраста, скорости роста оврага на разных стадиях его развития и т.д.

Психологическое пространство и время характеризуют основные структуры пространства и времени, связанные с восприятием и так называемыми перцептивными (вкусовыми, визуальными и т.д.) полями. Исследователями выявлены неоднородность перцептивного пространства, его асимметрия, эффект обратимости времени в бессознательных и транспсихических процессах, а также синхронизм психических процессов, состоящий в одновременном параллельном проявлении идентичных психических переживаний у двух или нескольких человек. Для иллюстрации психологического времени можно привести широко известное высказывание немецкого философа А. Шопенгауэра о том, что в детстве время идет очень медленно, в юности -быстрее, но все равно еле «передвигает ноги», в зрелом возрасте оно уже «идет в ногу» со старением, а в старости мчится, как стрела. Конечно же каждый человек испытывал моменты, когда время «мчится, как стрела» или «тянется, как резина». Проиллюстрировать различное восприятие пространства можно, например, напомнив о том, что одно и то же помещение одним людям может казаться большим, а другим - маленьким.

Кроме рассмотренных типов пространства и времени в литературе обсуждаются проблемы геологического, географического, социального и других типов пространств и времен, выделяются их специфические черты и характерные особенности. При этом обычно анализируются неоднородность пространственно-временных структур, специфические пространственные отношения между элементами, ритмы и темпы изменения, ускорение или замедление темпов развития рассматриваемых в конкретной отрасли естествознания объектов.

§ 5.2. Свойства пространства и времени

Самостоятельность пространства и времени

До настоящего времени нет единой модели пространства и времени, применимой во всех областях естествознания. Скорее можно говорить о выборе и создании подходящей модели пространства и времени для решения конкретных задач в разных отраслях науки о природе. Выбор некоторой модели пространства и времени или ее изменение имеет смысл лишь в случае, если это приведет к новой исследовательской программе, способствующей более глубокому проникновению в сущность изучаемого явления, получению нового знания.

Существуют разные подходы к решению проблемы о таких специфических свойствах пространства и времени, как самостоятельность, мерность, симметрия, обратимость, кривизна, соотношение физического и геометрического подходов [5, 10, 11, 13, 14]. Одно из наиболее обсуждаемых свойств пространства и времени связано с выявлением его самостоятельной сущности. Здесь говорят о двух концепциях: субстанциальной и реляционной (релятивистской).

Субстанциальная концепция подразумевает, что при описании природных процессов используются средства классической механики и пространство и время воспринимаются как нечто самостоятельное: пространство — некоторое пустое вместилище тел, а время — нечто протекающее равномерно и иначе называющееся длительностью. Само слово «субстанция» (от лат. substantia - сущность; то, что лежит в основе) подразумевает нечто относительно устойчивое или, другими словами, то, что существует само по себе, не зависит ни от чего другого.

В связи с самостоятельностью сущности пространства и времени возникает потребность в поиске специфических их свойств. В литературе эта проблема рассматривается применительно ко времени. Например, советский астрофизик H.A. Козырев в 1963 г. в своей работе «Причинная механика и возможность экспериментального исследования свойств времени» обратил внимание на следующие обстоятельства [10]. Большинство законов механики по отношению ко времени симметрично. Однако в действительности наблюдается направленное развитие мира. Несимметричность этого процесса обычно объясняется переходом систем из маловероятного состояния в более вероятное. Но реальная картина наблюдаемой Вселенной противоречит этому утверждению. Козырев предположил, что несимметричность есть свойство самого времени, а ход времени должен быть универсальной постоянной и определяться по отношению к некоторому инварианту, которым может служить пространство. Он ввел три аксиомы причинности: 1) причины и следствия всегда разделяются пространством; 2) причины и следствия всегда разделяются временем; 3) время обладает абсолютным свойством, отличающим будущее от прошедшего. Если это так, то в пространстве-времени должна существовать точка, не принадлежащая ни причине, ни следствию, а наличие хода времени должно служить объяснением того, что при изотропности пространства (независимости свойств физических явлений от направления) в нем всегда различаются правое и левое начала.

Реляционная (релятивистская) концепция используется в случае, если описание явлений действительно требует привлечения теории относительности А. Эйнштейна, где пространство и время существуют постольку, поскольку существует материя, т.е. если вдруг исчезнет материя, то исчезнет и пространство, и время. Эта концепция отрицает самостоятельную сущность пространства и времени, рассматривая время как отношение или систему отношений между физическими событиями. В ее рамках для времени наиболее ясно раскрываются отношения раньше-позже, очень важные с точки зрения причинно-следственного анализа.

Мерность пространства и времени

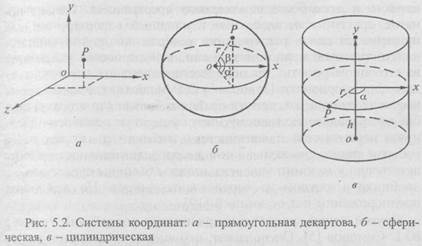
В литературе обсуждается такое свойство пространства и времени, как их мерность. Обычно под мерностью понимают количество замеров, которые следует сделать для однозначного определения места некоторой точки. Так, чтобы однозначно определить место точки в пространстве в фиксированный момент времени, необходимо и достаточно указать три ее координаты. В наиболее привычной прямоугольной декартовой системе координат это х, у, z - длина, ширина и высота (рис. 5.2, α); в сферической системе координат требуется указать радиус-вектор r и углы α и β (рис. 5.2, б); в цилиндрической системе - высоту h, радиус-вектор r и угол α (рис. 5.2, в).

Считается, что все материальные процессы и взаимодействия реализуются именно в пространстве трех измерений. В одномерном (линия) или двухмерном (плоскость) пространстве не могут происходить взаимодействия частиц и полей. Три измерения являются необходимым и достаточным минимумом, в рамках которого могут осуществляться все типы взаимодействий материальных объектов.

В настоящее время не известно каких-либо форм движения и взаимодействия, которые требовали бы четырех- или пятимерного пространства, и возможность таких процессов не вытекает ни из каких установленных законов природы.

В литературе нередки рассуждения о возможности существования пространств большего количества измерений. Так, в последнее время была выдвинута гипотеза о реальных 11 измерениях в области микромира в первые моменты рождения нашей Вселенной: 10 - пространственных и одно — временное; затем они образуют 4-мерный пространственно-временной континуум. Эта гипотеза связана со следующими обстоятельствами. В математике и физике широкое применение получило представление о многомерных (n -мерных) пространствах. Данная математическая абстракция играет важную роль. Каждая координата многомерного пространства может указывать на какое-то любое свойство рассматриваемой физической реальности - температуру, плотность, скорость, массу и т.д. Если число таких параметров вместе с пространственно-временными характеристиками равно п, то считается, что они образуют «-мерное пространство, а конкретные значения свойств определяются как точки в «-мерном пространстве. При достаточно большом количестве свойств и взаимосвязанных переменных можно прийти к понятию многомерного и даже бесконечномерного пространства. Однако понятие пространства здесь имеет условный характер, так как применяется для характеристики совершенно других свойств.

Что касается мерности времени, то чаще всего указывают на его одномерность: для определения времени достаточно задать одну координату. По мнению С.Т. Мелюхина, если бы время имело не одно, а два, три измерения и больше, то это означало бы, что параллельно нашему миру существуют аналогичные и никак не связанные с нашим миры-двойники, в которых те же события разворачиваются в той же последовательности. Соответственно у каждого человека должны были бы существовать двойники в каждом из параллельных миров. Но для таких предположений нет оснований [19].

Другой точки зрения придерживается российский географ Ю.Г. Симонов [5]. Он полагает, что вполне возможно предложить двухмерную модель времени, полезную для описания и изучения некоторого класса событий, и рассматривает ее на примере некоторых географических явлений. Здесь следует вспомнить о двух типах времени — солнечном и лунном. С фазами лунного и солнечного календарей могут быть связаны различные события. Известно, что эти векторы времени независимы и не совпадают по фазам, а их периоды не являются кратными друг другу. Так, изучая явления на Земле, можно отыскать среди них те, которые связаны лишь с гравитационными полями Земля - Луна и Земля - Солнце. Эти поля могут накладываться друг на друга, то суммируясь, то вычитаясь. В таком случае можно говорить об изучении гравитационной системы из трех тел. В такой системе количество векторов времени совпадает с количеством степеней свободы. Пусть в пространстве двух векторов времени ось х совпадает с вектором солнечного времени, а ось у — с лунным. В фазу новолуния силы лунного и солнечного притяжений складываются, а в фазу полнолуния — вычитаются. Поэтому в фазу новолуния максимальные гравитационные возмущения испытывают Земля и Солнце, а в фазу полнолуния — Луна и Солнце; минимум гравитационной напряженности Земли приходится на полнолуние, когда гравитационные поля вычитаются. Таким образом, на Земле гравитационная напряженность нарастает от полнолуния к новолунию, а затем убывает. При нарастании гравитационной волны возникают одни эффекты, а на фоне убывания (снятия) напряженности - другие. Так, тектонические трещины в разные фазы сжимаются и расширяются; процессы, связанные с трещинно-поровым давлением грунтовых вод, протекают с разной силой и т.д.

В общем случае, по мысли Симонова, векторов времени может быть не два, а больше. Выбор модели многомерного времени (в частности, определение количества временных векторов) удается осуществить довольно просто в том случае, когда изучаемые процессы причинно не зависят друг от друга и их можно представить себе как циклически проявляющиеся, причем циклы могут длиться не часами и сутками, а годами, столетиями и даже тысячелетиями.

Симметрия и асимметрия пространства и времени

Симметрия - одно из свойств пространства и времени. Это свойство заключается в переходе объектов в самих себя или друг в друга при осуществлении определенных преобразований. В наиболее широком смысле симметрия — свойство неизменности (инвариантности) отдельных сторон, процессов и отношений объектов относительно некоторых преобразований. Симметричными могут быть вещи, процессы, геометрические фигуры, математические уравнения, живые организмы, произведения искусства и т.д. Преобразования симметрии могут быть и реальными, и мысленными (пространственный сдвиг, вращение, зеркальное отражение в пространстве, зарядовое сопряжение -замена частицы на античастицу).

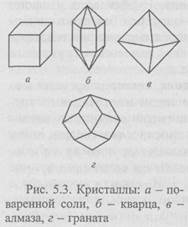
Представления о симметрии имеют большое значение практически во всех отраслях естествознания. Истоки этого понятия восходят к античным представлениям о гармонии, которые имели преимущественно эстетический смысл соразмерности, уравновешенности, упорядоченности, красоты и совершенства. Специальные научные разработки понятия симметрии начались в ХГХ в. в кристаллографии. Усилиями И. Гесселя (Франция), А. Шенфлиса (Германия), A.B. Гадолина и Е.С. Федорова (Россия) было создано учение о пространственной симметрии, в котором выделены 230 возможных групп симметрии. Внутренняя симметрия определяется молекулярным строением вещества, о чем свидетельствуют формы кристаллов природных минералов различного химического состава и их кристаллической решетки (рис. 5.3). Особенно совершенных форм можно добиться, выращивая искусственные кристаллы.

В окружающем нас мире преобладают два вида симметрии -зеркальная, или билатеральная, симметрия и радиально-лучевая [20]. Как оказалось, все, что растет или движется вертикально относительно земной поверхности, имеет радиально-лучевую симметрию в виде веера пересекающихся плоскостей симметрии, а все, что растет и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной симметрии (одна плоскость симметрии). Однако известно, что земное тяготение влияет лишь на внешнюю форму природных тел. Следовательно, форма любого объекта связана как с его внутренними свойствами, так и с внешними факторами, воздействующими на этот объект.

Соотношения внутренней и внешней симметрии получили отражение в принципе симметрии П. Кюри. В упрощенной форме он звучит так: симметрия порождающей среды накладывается на симметрию тела, образующегося в этой среде. Получившаяся в результате форма тела сохраняет только те элементы своей собственной симметрии, которые совпадают с наложенными на него элементами симметрии среды.

Идея симметрии лежит в основе многих исследований современной науки. Так, Ф. Клейн (Германия), рассматривавший различные геометрии как теории инвариантов определенных групп преобразований, внес существенный вклад в формирование современного понятия симметрии, тесно связав его с понятием инвариантности и теории групп. Теоремы Э. Нетера (Германия) позволили связать пространственно-временную симметрию (инвариантность) уравнений математической физики с сохранением фундаментальных физических величин - энергии импульса, момента количества движения. В дальнейшем исследование взаимосвязи принципов симметрии с законами сохранения стало одним из магистральных направлений развития физики.

В химии и биологии на первый план часто выходит асимметрия как определенное нарушение симметрии, особенно характерное для живых организмов на молекулярном и морфологическом уровнях их структурной организации. Эволюционное развитие материи от простых химических соединений к сложным органическим и биологическим системам обнаруживает общую тенденцию уменьшения степени симметрии и соответственно возрастание асимметрии. В.И. Вернадский видел в симметрии ключ к разделению живой и неживой природы, указывая на то, что правизна и левизна в мире кристаллов не играют принципиальной роли, а для живых организмов наблюдается иная картина. Л. Пастер показал, что в продуктах биохимических процессов преобладают либо правые, либо левые изомеры вещества. В обобщенном виде в биологии установлено, что пространство, занимаемое живым веществом, характеризуется асимметрией. Следует также отметить, что в мире кристаллов отсутствуют оси симметрии пятого, седьмого, восьмого и более высоких порядков, а в мире растений и простейших животных они встречаются достаточно часто.

Обратимость пространства и времени

Обратимость пространства и времени - свойство, тесно связанное с симметрией. Как известно, в каждую точку пространства можно снова и снова возвращаться. В этом отношении пространство является как бы обратимым. Что касается времени, то обычно подчеркивается его необратимость, означающая однонаправленное изменение от прошлого к будущему: нельзя возвратиться назад в какую-либо точку времени, но нельзя и перескочить через какой-либо временной промежуток в будущее. Отсюда делается вывод, что время составляет как бы рамки для причинно-следственных связей.

В более общем виде решение проблемы обратимости связано с рассмотрением двух противоположных концепций - статической и динамической [13].

Согласно статической концепции времени, события прошлого, настоящего и будущего существуют в известной мере одновременно. Кроме того, все физические законы инвариантны относительно замены знака времени, поскольку время в уравнениях движения классической и квантовой механики берется в квадрате. Это наводит на мысль, что все физические процессы могут происходить одинаково как в прямом направлении, так и в обратном. Если это действительно так, то имеется принципиальная возможность, перемещаясь во времени, оказываться в событиях прошлого или будущего, а также возвращаться из них в настоящее. Статическая концепция допускает возможность построения «машины времени» и некоторые другие эффекты и парадоксы. Так, если течение времени зависит от скорости движения его носителя, то можно принять парадокс близнецов в теории относительности, о котором говорилось ранее, а именно: возвратившийся из космического путешествия космонавт по существу попадает в свое будущее, а его брат, оставшийся на Земле, встречается со своим прошлым. Эти события происходят одновременно, т.е. в некоторый момент времени встречаются настоящее с прошлым и настоящее с будущим. В такой встрече отсутствует симметрия: один и тот же человек не встречается сразу и со своим прошлым, и со своим будущим.

Еще один пример. Свет от различных звезд долетает до нас за разные интервалы времени; следовательно, об их современном состоянии мы ничего не знаем, а изучаем их далекое прошлое, принимая его за настоящее.

В науках о Земле также обсуждаются такие явления. Еще в 1938 г. российский географ акад. К.К. Марков описал явление, которое он назвал метахронностью. Оно проявляется в том, что наступление и чередование фаз и стадий развития геосистем происходят несинхронно в разных частях земного шара, даже если эти геосистемы располагаются на одной широте. Например, установлено, что формирование ледникового щита Антарктиды началось значительно раньше, чем оледенение в Северном полушарии.

В настоящее время в науках о Земле обсуждают такое явление, как полихронность, которая предполагает одновременное наличие нескольких пластов времени в одном объекте. Все они существуют в настоящем, но, располагая их в некоторой хронологической последовательности, можно самые древние из них называть прошлым, средней давности - настоящим, а самые молодые - будущим. Полихронность свойственна многим природным явлениям. Поэтому статическая концепция не так уж нелепа, как ее иногда пытаются представить [5].

Динамическая концепция времени противоположна статической: в ней есть лишь настоящее, прошлое существовало, а будущее только еще будет существовать. К прошлому относятся все те события, которые уже осуществились и превратились в последующие. Будущие события — это те, которые возникнут из настоящих и непосредственно предшествующих им событий. Настоящее охватывает все те явления, которые реально существуют и способны к взаимодействию между собой. Взаимодействие возможно лишь при одновременном сосуществовании объектов.

В рамках динамической концепции невозможно построение «машины времени» для перемещения в прошлое и будущее. Если бы путешествие в прошлое было реально возможным, тогда, дойдя до некоторого момента, «машина времени» исчезла бы вместе с экипажем, поскольку в прошлом их реально не существовало. А при путешествии в будущее надо еще воссоздать некоторый будущий мир из ничего, куда-то «спрятав» существующий мир, чтобы затем возвратиться в него.

С этой концепцией связана неопределенность понятия настоящего, поскольку неясно, какой именно отрезок времени можно считать настоящим - миг, день или более продолжительное время. (Эта проблема стоит и перед представителями гуманитарных дисциплин, например современность в истории.) Представление о настоящем можно предельно сузить, выбирая все более и более короткие отрезки времени и доведя их до интервала, достаточного для того, чтобы его невозможно было принять за настоящее. Появляется ощущение, что нет не только прошлого и будущего, но и настоящего. Все, что было, — уже прошлое, все последующее - еще в будущем. Но настоящее может быть и расширено в зависимости от сопоставляемых интервалов и масштабов события до часа, дня, года и т.д.

Обычно говорят, что для объектов и явлений настоящее время охватывает тот интервал, в течение которого они физически могут взаимодействовать между собой путем обмена веществом и энергией. Если бы скорость распространения воздействий была бесконечной, то это настоящее представляло бы собой сколь угодно малый миг, дающий мгновенное сечение всех событий во Вселенной - настоящих, прошлых и будущих. Но скорость распространения воздействий конечна и, по современным представлениям, не превышает скорости света в вакууме. Поэтому физически проявляющееся во взаимодействиях настоящее материальных систем охватывает тот временной интервал, в течение которого они способны провзаимодействовать. Для элементарных частиц это будут очень малые отрезки времени, но для Галактики они возрастают до сотни тысяч лет. Внутри этого настоящего для крупных систем могут укладываться события прошлого, настоящего и будущего малых систем, существующих намного меньшее время. Только сейчас мы воспринимаем излучение от звезд и галактик, испущенное тысячи и миллионы лет назад. Взаимодействия между ними могут осуществляться в течение миллионов лет в обоих направлениях. Отсюда следует относительность понятия настоящего. При этом из систем будущего никаких воздействий и информации не может поступать, ибо эти системы еще не возникли, не обладают реальным существованием. Действие всегда происходит только в одном направлении: от прошлого к настоящему и от настоящего к ближайшему будущему, в которое настоящее переходит, но никогда наоборот. Принято считать, что последнее исключается законом причинности.

Геометрические свойства пространства

Геометрический анализ пространства опирается прежде всего на исторический опыт землепользования. Первые научные геометрические представления выражены в евклидовой геометрии, по которой пространство характеризуется трехмерностью и изотропностью (независимостью свойств от направления), а прямая есть кратчайшее расстояние между двумя точками. Геометрия Евклида исходит из пяти аксиом, или постулатов. Более всего споров у математиков вызывал пятый постулат, в соответствии с которым из одной точки на плоскости можно провести только одну прямую, которая не будет пересекаться с данной. В начале XIX в. немецкий математик К.Ф. Гаусс признал, что если этот постулат "заменить другими аксиомами, то можно построить новую геометрию. Такие новые геометрии были построены Н.И. Лобачевским (Россия), Б. Риманом (Германия) и Я. Больяем (Венгрия). Так, Лобачевский и Больяй допустили, что существует множество прямых, которые не пересекутся с данной. Риман, напротив, заменил пятый постулат на аксиому, согласно которой через точку, лежащую вне данной прямой на плоскости, нельзя провести ни одной параллельной, все они будут пересекаться с данной.

Эти представления наглядно иллюстрируются на двухмерных поверхностях. Евклидова геометрия реализуется на плоскости, геометрия Римана - на поверхности сферы, на которой прямая линия выглядит как отрезок дуги большого круга, центр которого совпадает с центром сферы. Геометрия Лобачевского реализуется на так называемой псевдосфере. Поскольку пространство имеет три измерения, то для каждой геометрии вводится понятие кривизны пространства (рис. 5.4). В евклидовой геометрии кривизна нулевая, у Римана - положительная, у Лобачевского и Больяя - отрицательная, поскольку на основании пятой аксиомы доказывается теорема о сумме углов треугольника. В геометрии Евклида, как известно, она равна 180°, у Римана - она больше 180°, а у Лобачевского — меньше.

В трехмерном неевклидовом пространстве кривизна пространства понимается как отступление его метрики от евклидовой, что точно описывается языком математики, но невозможно представить как-то наглядно. Впоследствии Риман показал единство и непротиворечивость всех неевклидовых геометрий, частным случаем которых выступает геометрия Евклида.

Рассматривая физические и геометрические свойства пространства и времени, полезно затронуть вопрос об их соотношении и предпочтении той или иной геометрии для построения конкретных физических моделей явлений. С этой точки зрения интересна позиция А. Пуанкаре, который утверждал, что, если пространство с любой произвольно заданной геометрией дополнено законами физики, оно может быть принято для описания изучаемого явления. Аналогичной точки зрения придерживался А. Эйнштейн. Но если Пуанкаре предлагал выбирать относительно простую геометрию пространства и дополнять ее сравнительно сложными описаниями физических законов, то Эйнштейн, наоборот, предлагал более сложную геометрию дополнять сравнительно простыми физическими законами [14]. Так, в теории относительности Эйнштейна используется геометрия Римана. Эту возможность наглядно иллюстрирует следующий мысленный эксперимент [22, 23]. Пусть лифт покоится в отсутствие гравитационного поля (рис. 5.5, а). В стенке лифта сделано отверстие А, через которое луч света падает на его противоположную сторону; линия AB - прямая. Лифт начинает движение вверх с ускорением g. За время, пока свет проходит расстояние между стенками, лифт смещается вверх, и луч света попадает не в точку В, а в точку С (рис. 5.5, б). Линия АС сохраняет свойство быть кратчайшим расстоянием между двумя точками, но это будет не прямая, а так называемая геодезическая.

§ 5.3. Методы оценки пространства

Размеры микрообъектов

Нас окружают объекты, размеры которых несопоставимы друг с другом: молекулы и Солнечная система, атомы и галактики и т.д. Все они расположены в пространстве, и, следовательно, можно оценить расстояния, связанные с этими объектами. Приведем некоторые приблизительные оценки, позволяющие более уверенно ориентироваться в окружающем пространстве [3, 7, 15].

Минимально видимая глазом длина сопоставима с толщиной волоса - около 0,1 мм. Если быть более точным, то невооруженным глазом с расстояния наилучшего видения (около 25 см) наблюдатель со средней остротой зрения может отличить одну мелкую частицу (или деталь объекта) от другой, лишь если они отстоят друг от друга на расстоянии около 0,08 мм. Усилить наше зрение может лупа - собирающая линза - или система линз с небольшим фокусным расстоянием (10-100 мм). С ее помощью можно добиться увеличения от 2 до 50 раз, т.е. объект можно рассмотреть в среднем в 10 раз детальнее.

Свойство линзы или системы линз давать увеличенные изображения предметов известно с XVI в. Оптический микроскоп впервые успешно применил в научных исследованиях англичанин Р. Гук, установивший в 1670-х гг. клеточное строение животных и растительных тканей. Примерно в это же время голландский ученый А. Левенгук открыл с помощью оптического микроскопа микроорганизмы. Развитию методов микроскопических исследований существенно способствовала разработка теории образования изображений несамосветящихся объектов в микроскопах немецким физиком Э. Аббе (вторая половина XIX в.).

Современный оптический микроскоп дает увеличение примерно в 100-1000 раз. Следовательно, размеры объектов, которые можно увидеть в такой микроскоп, составляют 0,0001 мм (10^-7м). Различные типы оптических микроскопов предназначены для обнаружения и изучения микроорганизмов (бактерий, микроскопических грибов, водорослей и вирусов), органических клеток, мелких кристаллов, определения и детального изучения минералов, минерального состава и структуры горных пород и т.д.

Возможности оптических микроскопов ограничены разрешающей способностью, т.е. способностью давать раздельные изображения двух близких друг к другу точек объекта. Дело в том, что из-за дифракции света изображение точки представляет собой светлое пятно, окруженное кольцами, и после некоторого увеличения изображения двух точек начинают сливаться. В видимом свете ничего нельзя рассмотреть при увеличении объекта более чем в 1500-2000 раз, поскольку длина волны видимого света становится больше изучаемого объекта.

Для того чтобы рассмотреть более мелкие объекты, используют электронный микроскоп - прибор, в котором для получения увеличенного изображения используется электронный пучок. Разрешающая способность электронного микроскопа в сотни раз выше, чем у оптического микроскопа. Электронные микроскопы позволяют получить с помощью наблюдения и фотографирования многократно увеличенные объекты (вплоть до 10 раз) и увидеть объекты размером 10^-9 м. Эти приборы дают возможность при определенных условиях рассмотреть микроструктуру тел (вплоть до атомно-молекулярного уровня) и т.п. Физические основы электронно-оптических приборов были заложены ирландским математиком У.Р. Гамильтоном почти за 100 лет до появления электронных микроскопов, которые стали создаваться в первой половине XX в., а широкое применение в естествознании получили уже во второй половине XX в. Высокие разрешения этих микроскопов достигаются благодаря чрезвычайно малой длине волны электронов. Несколько большие подробности объектов можно рассмотреть лишь косвенными методами. Например, в настоящее время применяется метод изучения объектов с помощью рассеяния электронов.

Размеры макрообъектов

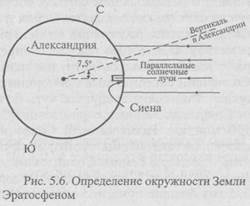
Обратимся к макрообъектам. Если допустить, что рост человека составляет в среднем 1,5-2 м, то эта величина превышает диаметр волоса на четыре порядка. Размеры большей части предметов, окружающих нас, сопоставимы с размерами человеческого тела, иначе было бы трудно иметь с ними дело. Расстояния до объектов, находящиеся на больших расстояниях (холм, лес, поле и т.д.), можно оценить шагами, т.е. по существу сопоставить их с размером своего тела. В таких случаях расстояние составляет от нескольких километров до нескольких десятков километров. Таким образом, непосредственное восприятие человеком расстояний возможно в диапазоне от 0,1 мм до приблизительно 100 км. Оценка размеров континентов, а тем более окружности Земли вряд ли возможна с помощью шагов. В этом случае целесообразно поступить так. Если известны средняя скорость движения некоторого вида транспорта (поезда, машины, самолета и пр.) и время в пути, можно получить представление о преодоленном расстоянии: если ехать из одного пункта в другой со скоростью 100 км/ч в течение 7 ч, то ясно, что было преодолено расстояние 700 км; если самолет за 9 ч долетает из Москвы до Петропавловска-Камчатского при средней скорости 800-850 км/ч, то эти населенные пункты разделены расстоянием приблизительно 7500 км. Чтобы облететь вокруг Земли, самолету потребовалось бы примерно в 5 раз больше времени, поскольку ее окружность составляет около 40 000 км. Весьма точно окружность Земли и ее радиус удалось оценить еще в античное время Эратосфену. Он заметил, что в день летнего солнцестояния 21-22 июня в районе г. Сиены (Асуан, Египет) лучи Солнца падают отвесно, а в Александрии, отстоящей на 800 км севернее, угол падения 7,5° (рис. 5.6). Из простейших тригонометрических расчетов следует, что окружность Земли составляет 40 000 км, а ее диаметр — около 12 000 км. Оценить расстояние до небесных тел можно также с помощью очень простых способов. Ближайшим небесным телом для нас является Луна. Еще во II в. до н.э. Гиппарх измерил угол, под которым видна тень, отбрасываемая Землей на Луну во время лунного затмения, а зная диаметр Земли, он довольно точно определил расстояние от Земли до Луны. В настоящее время для таких целей используют радиолокацию. Сигнал радара направляют на объект и измеряют время, протекшее от посылки сигнала до возвращения отраженной волны. Для Луны это время составит 2,6 с; следовательно, в одну сторону сигнал летел 1,3 с. Поскольку волна радара имеет ту же природу, что и световая, и распространяется со скоростью 300 000 км/с, можно заключить, что расстояние Земля Луна приблизительно 400 000 км.

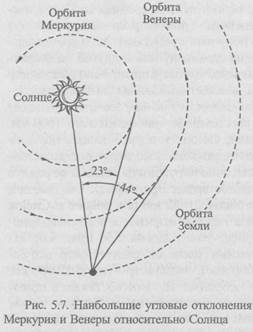
Наблюдения за движением планет позволяют определить относительные размеры их орбит. Так, Меркурий всегда наблюдается близко от Солнца, никогда не далее 23°, т.е. радиус орбиты Меркурия равен 0,38 радиуса земной орбиты (немногим более 1/3 ее радиуса). Аналогичным способом находим радиус орбиты Венеры - 0,7 радиуса земной орбиты (немногим более 2/3 от него). Таким образом, можно построить картину Солнечной системы, соблюдая найденные пропорции (рис. 5.7).

Для того чтобы узнать истинный радиус орбит планет, следует определить расстояние только до одной из них, а остальные рассчитать по уже известной пропорции. Здесь также пользуются радарным методом. Например, до Венеры время между испусканием и возвращением сигнала составляет 5-15 мин в зависимости от того, где находятся Земля и Венера на своих орбитах. Следовательно, расстояние до Венеры порядка миллионов километров. После того как было определено расстояние Венера - Земля, оказалось нетрудно найти и другие расстояния в Солнечной системе, зная пропорции и относительные размеры орбит. Так, свету требуется чуть больше 8 мин, чтобы дойти от Солнца до Земли, т.е. расстояние Земля — Солнце составляет 150 млн км. Размеры всей Солнечной системы таковы, что свету для того, чтобы пройти ее, нужно 11ч. Несложно оценить и размеры самого Солнца. Оно кажется нам таким же, как Луна, но оно в 375 раз дальше, и диаметр его должен быть в 375 раз больше лунного: он равен 1,4 млн км.

Межзвездные пространства

Оценить расстояния до звезд можно несколькими методами. Один из них связан с измерением светимости звезд. Предположим, что звезды имеют размеры, сопоставимые с размерами Солнца. Однако одни из них светят ярче, а другие - слабее, поскольку одни звезды ближе к нам, другие - дальше. Это позволяет вычислить расстояния до звезд. Для этого надо учесть, что если одно из двух одинаково ярких тел находится на расстоянии, в n раз большем, чем другое, то более близкое тело кажется в n раз ярче. Так, интенсивность света Солнца в (миллион) раз ярче Сириуса, т.е. Сириус находится в миллион раз дальше от Земли, чем Солнце. Яркость других звезд, например семи звезд ковша Большой Медведицы, в 9 раз меньше яркости Сириуса; следовательно, они должны находиться еще в 3 раза дальше.

Используя этот метод, можно было бы найти расстояния до всех звезд. Однако мы не обязаны верить «на слово», что звезды - такие же тела, как и Солнце. Поэтому полезно использовать какой-либо иной метод. В 1830-х гг. для этой цели был предложен метод параллаксов. Этот метод основан на простейшем способе измерения расстояния до какого-либо недоступного предмета: его визируют из двух разных точек и затем определяют, как изменяется направление, в котором он виден. Например, отдаленное дерево будет видно немного в ином направлении, если пройдем несколько шагов перпендикулярно линии, соединяющей дерево и наблюдателя, и, чем дальше дерево, тем меньше изменится направление, в котором оно видно. Исхода из этого изменения, вычисляют расстояние до дерева. При измерении расстояний до звезд используют эффект вращения Земли вокруг Солнца (рис. 5.8). Так, зимой мы смотрим на звезду из точки, которая на 300 млн км удалена от летней точки наблюдения. При этом для наблюдателя звезда переместится по небесному своду на расстояние, равное диаметру земной орбиты. Иначе говоря, он увидит звезду, сместившуюся на угол, под которым виден диаметр земной орбиты со звезды. Эти смещения крайне малы, но уже более 150 лет назад были созданы инструменты, способные измерять столь малые смещения. Оказалось, что таким методом можно измерить расстояние звезд, отстоящих не более чем на 50 световых лет. (Световой год - единица измерения межзвездных расстояний; путь, который свет проходит за год, т.е. 9,46 · 10¹² км.) На этом расстоянии находится около 300 звезд. Ближайшие от нас звезды (Проксима, Альфа в созвездии Центавра) находятся на расстоянии приблизительно 4 световых лет.

Смещение множества звезд слишком мало, чтобы его можно было измерить. При этом оценку межзвездных расстояний по светимости выполняют путем сравнения звезд одного цвета, которые не слишком различаются по размеру.

Оценив межзвездные расстояния, можно оценить протяженность пустого пространства между нашей Солнечной системой и одной из ближайших звезд - Сириусом: оно в 1 млн раз больше расстояния от Земли до Солнца, т.е. порядка 10¹⁴ км. Свету требуется примерно 10 лет, чтобы пройти это расстояние. Если учесть те несколько часов, за которые свет проходит Солнечную систему, то можно получить представление о расстояниях до ближайших звезд.

Оценим распределение звезд в пространстве. Наблюдая за звездным небом, можно увидеть, что слабых звезд гораздо больше, чем ярких, и они распределены по небу неравномерно.

В самом Млечном пути или около него слабых звезд значительно больше, чем в отдаленных участках неба. Если смотреть в направлении, сильно удаленном от Млечного пути, можно заметить некоторое количество ярких звезд и почти не увидеть очень слабых. Таким образом, звезды не распределены в пространстве равномерно, а сосредоточены на участке, имеющем вид плоского диска. Наша Солнечная система находится где-то в этом диске.

Можно оценить размеры диска, внутри которого находятся все звезды, видимые нами на небе. Известно, что яркость звезд, еще видимых в направлении плоскости Млечного пути, в 100 раз слабее, чем звезд, видимых в перпендикулярном направлении; следовательно, радиус диска должен примерно в 10 раз превышать его толщину. Яркость наиболее слабых звезд Млечного пути приблизительно в 100 млн раз меньше яркости Сириуса, т.е. они должны находиться в 10 000 раз дальше от Земли, чем Сириус, — на расстоянии 100 000 световых лет. Таким образом, из распределения слабых и ярких звезд по небу следует, что звезды образуют круговой диск диаметром 10⁵ световых лет и толщиной 10 световых лет. Причем Солнечная система находится примерно на середине радиуса. Это скопление звезд называется галактической системой или нашей Галактикой. Среднее расстояние между звездами в ней — около 10 световых лет. Это позволяет оценить количество звезд в Галактике - около 50 млрд. Другие оценки дают цифру 100 млрд звезд.

В настоящее время известно, что в состав Галактики входят не только звезды, но также газы и пыль, которые затрудняют применение рассмотренного метода измерения расстояний. Звезда, видимая через слой газа и пыли, кажется слабее, и мы можем ошибочно заключить, что она дальше от нас, чем на самом деле. Эту трудность позволяют преодолеть другие методы. С их помощью установлено, что звезды сосредоточены в больших спиральных рукавах, выходящих из центра диска и закрученных в его плоскости.

Межгалактические пространства

Кроме нашей Галактики существуют и другие звездные скопления, например туманность Андромеды, которая при наблюдении в сильный телескоп выглядит как скопления звезд, расположенных в виде такой же дискообразной спирали, как наша Галактика. Количество таких галактик очень велико. Расстояние до них может быть оценено исходя из кажущейся яркости объектов. Например, полная яркость туманности Андромеды приблизительно такая же, как у средней звезды, удаленной на 10 световых лет. Мощные телескопы показывают, что звезд в этой галактике примерно столько же, как и в нашей,- около 50 млрд. В таком случае эта туманность в 50 млрд раз ярче отдельной звезды нашей Галактики. Тогда расстояние до туманности Андромеды должно быть в корень из (50 х 10⁹) раз больше, чем до ближайших звезд, т.е. определяется как произведение 10 световых лет на корень из (50 х 10⁹), что дает около 2 млн световых лет. Получается, что расстояние от нашей Галактики до соседней приблизительно в 20 раз больше диаметра нашей Галактики. Свет, приходящий от туманности Андромеды, покинул ее тогда, когда нашу Землю населяли еще не люди, а их обезьяноподобные предки. Множество спиральных туманностей можно увидеть с помощью телескопов. Известно о миллионах таких туманностей, и расстояния между ними достигают нескольких миллионов световых лет.

Возникает вопрос: а есть ли предел у самой Вселенной? На него помогает ответить открытый в первой половине XX в. факт «разбегания» галактик. Анализ спектров галактик показал: чем дальше находятся от нас галактики, тем быстрее они удаляются. Дело в том, что при изучении спектров звезд было выявлено отсутствие в них определенных частот - темные линии в спектре, которые расположены как раз на тех местах, где находился бы свет соответствующей частоты, если бы он не поглощался холодным газом на поверхности звезд. Например, в большинстве звездных спектров наблюдаются две темные линии в фиолетовой части, указывающие на поглощение газообразным кальцием. Те же темные линии в спектрах наблюдаются в спектрах галактик, так как их излучение представляет собой сумму излучения всех входящих в них звезд. Однако эти линии находятся не при ожидаемой частоте, а смещены в сторону меньших частот. Такое смещение частоты можно истолковать как следствие движения объекта относительно наблюдателя, поскольку при удалении источника света от наблюдателя его частота уменьшается (можно сравнить со звуком автомобильного сигнала, который кажется ниже, когда автомобиль удаляется от нас). Смещение частоты пропорционально скорости и поэтому может служить для определения скорости удаляющихся объектов.

Смещение частоты света от отдаленных галактик трактуют как доказательство того, что они удаляются от нас. Скорость этого движения пропорциональна расстоянию до галактики. Движение ближайшей галактики, например туманности Андромеды, почти невозможно обнаружить, но галактики, отстоящие от нас на 100 млн световых лет, удаляются со скоростью около 3000 км/с. Связь между скоростью и расстоянием впервые установил американский астроном Э.П. Хаббл в 1929 г. На рис. 5.9 представлена последовательность оценок расстояний, расположенных в порядке их возрастания. В настоящее время наиболее сильные телескопы позволяют различать галактики, удаленные на 3 млрд световых лет и «убегающие» от нас со скоростью 90 000 км/с, что составляет почти треть скорости света. В начале 1960-х гг. были открыты квазары. Самый далекий из известных ныне квазаров находится от нас на расстоянии около 8 млрд световых лет.

Таковы размеры доступной в настоящее время нашим исследованиям части Вселенной.

Таким образом, можно создавать все более и более мощные телескопы, пытаясь наблюдать удаленные галактики, однако последние будут «убегать» от нас со скоростью, все более приближающейся к скорости света. Чем ближе скорость объекта к световой, тем меньше будет его яркость, тем менее заметным он станет. Поэтому если даже и существует множество галактик, удаленных на расстояние, большее 10 млрд световых лет, нам не удастся их увидеть: они удаляются от нас настолько быстро, что их свет никогда не сможет достичь Земли.

§ 5.4. Методы оценки времени

Малые интервалы времени

Оценим временные интервалы различной длительности [3, 7, 8, 15]. Сравнительно малой и хорошо воспринимаемой человеком единицей времени является 1 с - это приблизительно интервал между двумя ударами сердца. Наиболее короткий промежуток времени, воспринимаемый человеком, составляет 0,1 с (длительность щелчка пальцами). Также известна способность глаза различать отдельные изображения. Так, если кинопленку протягивать со скоростью менее 14 кадров в 1 с, то человек различит отдельные кадры. Смена изображения со скоростью 24 кадра в 1 с приводит к возможности видеть непрерывное изменение явлений, а 25-й кадр уже не воспринимается глазом.

Развитие науки и человеческой практики привело к потребности измерять время, составляющее тысячные, миллионные, миллиардные и даже биллионные доли секунды. Например, в течение 1 с бегун продвигается на 5—10 м и совершает много сложных движений, из которых каждое длится лишь сотые доли секунды; от правильности построения этих движений зависит его победа. В автомобильном двигателе вал делает несколько тысяч оборотов в 1 мин: в течение сотых долей секунды в двигателе резко меняются давление и механическое напряжение, испытываемое отдельными деталями.

Для определения географических координат, в первую очередь долготы местности, необходимо точно знать время в измеряемой точке. Ошибка в отсчете времени, равная 1 мин, при определении долготы на широте экватора соответствует искажению расстояния на 27,6 км, ошибка в 1 с влечет за собой искажение на 460 м и ошибка в 0,001 с - на 0,46 м. В ряде случаев определять координаты требуется с высокой точностью. Например, в геологии обсуждается проблема перемещения одних материков по отношению к другим. Скорость перемещения обычно не превышает несколько сантиметров в год. Чтобы измерить перемещение одной точки по отношению к другой на земном шаре, следует производить замеры в течение нескольких лет, обеспечивая погрешность определения моментов времени порядка тысячных долей секунды.

Для того чтобы измерять время, требуется выбрать систему отсчета, научиться хранить и передавать точное время. Долгие годы единственной системой отсчета было вращение Земли вокруг своей оси и вокруг Солнца, но оказалось, что этот эталон времени не всегда достаточно точен. Дело в том, что орбита Земли представляет собой эллипс, в одном из фокусов которого находится Солнце. Вследствие этого Земля то ближе, то дальше от него и соответственно движется то быстрее, то медленнее. Движение Земли вокруг своей оси также неравномерно, в частности сезонная нерегулярность достигает 0,001 с. Поэтому в 1960-х гг. Международный комитет мер и весов принял решение использовать в качестве эталона астрономические атомно-лучевые цезиевые часы. При этом 1 с = 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.

Обычный стрелочный секундомер измеряет промежутки времени между двумя моментами с погрешностью до 0,1 с. Электрический стрелочный секундомер с вращающимися механическими частями позволяет производить отсчет промежутков времени с погрешностью до 0,01 с. Оценка более быстрых процессов с помощью механических устройств затруднена, так как их детали обладают большой инерцией. Современные технологии, основанные на измерении колебаний атомов, позволяют достигать точности в пределах 10^-12 - 10^-14с, т.е. с максимальной ошибкой в 1 с при измерении интервалов от 30 тыс. до 3 млн лет.

Для изучения быстрых процессов существует достаточно большое количество методов: специальная киносъемка, оптические устройства, электронные измерительные схемы и т.д. Для исследования ряда чрезвычайно быстрых ядерных процессов применяются различного типа счетчики (Гейгера - Мюллера, сцинцилляционный и др.).