Системность в естествознании

§ 4.1. Системный подход

Системность и уровни системности труда

Особенностью современного естествознания является осознанное внедрение идей системности во все его отрасли. Системность реализуется в рамках системного подхода, т.е. исследований, в основе которых лежит изучение объектов как сложных систем. Разработкой системных идей занимается системный анализ (специальная синтетическая наука, в центре которой находится изучение сложных систем). Особый вклад системного анализа, а более широко и системного подхода, в решение различных проблем обусловлен тем, что он позволяет, во - пеpвых, выявить те факторы и взаимосвязи, которые могут оказаться весьма существенными; во-вторых, видоизменять методику наблюдений и эксперимент таким образом, чтобы включить эти факторы в рассмотрение; в-третьих, осветить слабые места гипотез и допущений. Системный анализ с его акцентом на проверку гипотез посредством экспериментов и строгих выборочных процедур - мощный инструмент гибкого, но строгого исследования сложных явлений.

Вероятно, мышление и процесс познания всегда были системными, хотя и неосознанно. Представления о системности отражены в привычных для нас оборотах речи: «Солнечная система», «нервная система», «система уравнений», «общественно-политическая система», «система взглядов и убеждений», «отопительная система». Важной предпосылкой перехода на уровень осознанной системности и разработки системного подхода послужило появление новых задач в естествознании, связанных с изучением организации и функционирования сложных объектов, а также оперированием системами, границы и состав которых не столь очевидны.

В настоящее время общепризнано, что системные представления полезны и важны в решении проблем в различных сферах деятельности. Однако часто исследователи, назвав объект системой и декларируя использование системного подхода, строят свое изучение на обычной, традиционной для конкретной области основе. Исследование будет осознано системным при выполнении требований системной методологии, вырабатываемой в рамках системного подхода.

Для того чтобы осознать необходимость системности во всех отраслях человеческой деятельности, обратимся к практической деятельности человека, рассмотрев последовательное формирование трех уровней системности труда: механизацию, автоматизацию и кибернетизацию. Каждый из этих уровней, надстраиваясь на предыдущем, включает его в себя и не отменяет его полностью [22].

Механизация - простейший способ повышения эффективности труда. С помощью механизмов и машин один человек выполняет физическую работу, посильную многим людям. Механизация, позволяя решать многие проблемы, однако, имеет естественный предел - работой механизмов управляет человек, а его возможности ограничены физиологически: лопату нельзя делать слишком широкой; машина не должна иметь слишком много индикаторов и рычагов управления и т.д.

Решение проблемы состоит в том, чтобы исключить участие человека из конкретного производственного процесса, т.е. возложить на машины выполнение не только самого процесса, но операций по его регулированию. Автоматизация — способ повышения производительности труда с помощью автоматов, т.е. технических устройств, реализующих указанные две функции. В жизнь вошли торговые и игровые автоматы, автоматическая телефонная связь, в промышленности функционируют автоматические линии, цеха и заводы, развивается промышленная и транспортная робототехника. Большие возможности представляют перестраиваемые, многофункциональные автоматы, управляемые компьютерами.

Однако автоматизировать можно только те работы, которые хорошо изучены, подробно и полно описаны, о которых точно известно, что, в каком порядке и как надо делать в каждом случае, точно известны все возможные случаи и обстоятельства, в которых может оказаться автомат. Автомат реализует определенный алгоритм, который в какой-то своей части может быть неправилен или неточен либо не предусматривает всех возможных ситуаций; в этих случаях автомат не соответствует целям его создания.

Такие проблемы возникают в процессе руководства человеческими коллективами, при проектировании, эксплуатации и управлении крупными техническими комплексами, при вмешательстве (например, медицинском) в жизнедеятельность человеческого организма, при воздействии человека на природу, т.е. в тех случаях, когда приходится сталкиваться с неформализуемостью процессов, происходящих в системе, и непредвиденностью некоторых внешних условий.

Кибернетизация — совокупность способов решения возникающих при этом проблем - третий уровень системности практической деятельности человека. Кибернетика первой стала претендовать на научное решение проблем управления сложными системами. Поэтому, когда автоматизация (т.е. формальная алгоритмизация) невозможна, следует использовать человеческий интеллект, т.е. способность ориентироваться в незнакомых условиях и находить решение слабо формализованных задач. При этом человек выполняет операции, которые не поддаются формализации: экспертная оценка или сравнение неколичественных вариантов, взятие на себя ответственности и т.д. На таком принципе строятся автоматизированные (в отличие от автоматических) системы управления, в которых формализованные операции выполняют автоматы и компьютеры, а неформализованные операции - человек. Дальнейший путь кибернетизации обычно связывают с попытками хотя бы частично смоделировать интеллектуальные возможности человека.

Свойства и классификация систем

Центральное место в системном подходе занимает понятие «система». Поэтому разные авторы, анализируя это понятие, дают определения системы с различной степенью формализации, подчеркивая разные ее стороны [29]. Мы определим систему как совокупность элементов, находящихся в отношениях и связях друг с другом и образующих некую целостность.

Системам независимо от их природы присущ ряд свойств [30]:

◊ целостность — принципиальная несводимость свойств составляющих ее элементов и невыводимость из последних свойств целого, а также зависимость каждого элемента, свойства и отношения системы от его места внутри целого, функции и т.д. Например, ни одна деталь часов отдельно не может показать время, это способна сделать лишь система взаимодействующих элементов. Появление у системы специфических свойств, не присущих ни одному элементу, называется эмерджентностью;

◊ структурность - возможность описания системы через установление ее структуры или, проще говоря, сети связей и отношений системы. Структурность также подразумевает обусловленность свойств и поведения системы не столько свойствами и поведением ее отдельных элементов, сколько свойствами ее структуры. Простейший пример: разные свойства алмаза и графита определяются различной структурой при одинаковом химическом составе;

◊ взаимозависимость системы и среды, выражающаяся в том, что система формируется и проявляет свои свойства в процессе взаимодействия со средой, являясь при этом ведущим активным компонентом взаимодействия. Действительно, сложно что-либо сказать о некоторой системе, если она себя никак не проявляет;

◊ иерархичность систем, т.е. каждый компонент системы в свою очередь может рассматриваться как система, а исследуемая в конкретном случае система представляет собой один из компонентов более широкой системы. Например, живая клетка многоклеточного организма является, с одной стороны, частью более общей системы - многоклеточного организма, а с другой - сама имеет сложное строение и, безусловно, должна быть признана сложной системой;

◊ множественность описания системы, т.е. в силу принципиальной сложности каждой системы ее познание требует построения множества различных моделей, каждая из которых описывает лишь определенный аспект системы. Например, любое животное имеет части тела, которые могут рассматриваться как его элементы; это животное можно рассмотреть как совокупность скелета, нервной, кровеносной, мышечной и других систем; наконец, его можно проанализировать как совокупность химических элементов.

Известно большое количество классификаций систем [22, 30]. Так, системы можно разделить на материальные и абстрактные. Материальные системы представляют собой целостные совокупности материальных объектов и в свою очередь делятся на системы неорганической природы (физические, химические, геологические и др.) и на живые (начиная с простейших биологических систем через организмы, виды, экосистемы к социальным системам). Абстрактные системы являются продуктом человеческого мышления. Это разного рода понятия, гипотезы, теории, концепции и т.д. По другому основанию можно разделить системы на статические, состояние которых в течение времени не меняется (например, газ в герметичной емкости и находящийся в равновесии), и динамические, состояние которых изменяется (земная кора, организм, биогеоценоз и т.д.). Еще одна классификация делит системы на детерминированные, в которых значение переменных системы в некоторый момент времени позволяет установить состояние системы в любой другой момент, и вероятностные (стохастические), в которых с определенной вероятностью можно предсказать направление изменения переменных. Классификация по характеру взаимоотношения системы и ее среды делит системы на закрытые, которые не ведут обмена со своей средой веществом и энергией; полуоткрытые, обменивающиеся только энергией, и открытые, которые обмениваются и энергией, и веществом.

Эволюция системных представлений

Многие исследователи полагают, что системность всегда, осознанно или неосознанно, была методом любой науки [22, 30]. Считается, что первые представления о системах возникли в античности. В трудах Евклида, Платона, Аристотеля, стоиков разрабатывались идеи системности знания, аксиоматического построения логики, геометрии. Представления системности бытия развивались в концепциях Б. Спинозы и Г.В. Лейбница, в научной систематике XVII—XVIII вв., стремившейся показать естественно-научную системность мира; примером такой систематики может служить классификация растений и животных К. Линнея. Принципы системной природы знания разрабатывались в немецкой классической философии. Так, согласно И. Канту, научное знание есть система, в которой целое главенствует над частями, Ф.В. Шеллинг и Г.В.Ф. Гегель трактовали системность познания как важнейшее требование диалектического мышления.

Первым в явной форме вопрос о научном подходе к управлению сложными системами поставил в 1834—1843 гг. М.А. Ампер, который выделил специальную науку об управлении государством и назвал ее кибернетикой. Почти в то же время польский философ Б. Трентовский начал читать курс лекций, изложенный им в книге «Отношение философии к кибернетике как искусству управления народом». Трентовский ставил целью построение научных основ практической деятельности руководителя («кибернета»). Он подчеркивал, что управление будет действительно эффективным, если учитывает все важнейшие внешние и внутренние факторы, влияющие на объект управления. Главная сложность в управлении, по Трентовскому, связана с неопределенностью поведения людей. Он указывал, что общество, коллектив и сам человек - это система, единство противоречий, разрешение которых и есть развитие. Поэтому «кибернет» должен уметь, исходя из общего блага, одни противоречия примирять, другие - обострять, направляя развитие событий к нужной цели.

Общество середины XIX в. оказалось не готовым воспринять идеи кибернетики. Лишь в конце XIX в. системная проблематика снова появилась в поле зрения науки. На этот раз внимание было сосредоточено на вопросах структуры и организации систем. В 1890 г. Е.С. Федоров опубликовал свои выводы о том, что может существовать только 230 разных типов кристаллической решетки, хотя любое вещество при определенных условиях может кристаллизоваться. Безусловно, это открытие касалось прежде всего минералогии и кристаллографии, но его более общий смысл и значение отметил еще Федоров. Важно было осознать, что все невообразимое разнообразие природных тел реализуется из ограниченного и небольшого количества исходных форм. Это верно и для лингвистических устных и письменных построений, архитектурных конструкций, строения вещества на атомном уровне, музыкальных произведений, других систем. Развивая системные представления, Федоров выявил и некоторые закономерности развития систем, в частности он установил, что главным средством жизнеспособности и прогресса систем является не их приспособленность, а способность к приспособлению («жизненная подвижность»), не стройность, а способность к повышению стройности.

Следующий шаг в изучении системности как самостоятельного предмета связан с именем A.A. Богданова, в 1913—1917 гг. опубликовавшего свою книгу «Всеобщая организационная наука (тектология)», где он высказал идею о том, что все существующие объекты и процессы имеют определенный уровень организованности [5]. В отличие от естественных наук, изучающих специфические особенности организации конкретных явлений, тектология должна изучать общие закономерности организации для всех уровней организованности, рассматривая все явления как непрерывные процессы организации и дезорганизации, исследовать закономерности развития организации, соотношения устойчивого и изменчивого, значение обратных связей и собственных целей организации (которые могут как содействовать целям высшего уровня организации, так и противоречить им), роль открытых систем. Богданов отмечал, что уровень организации системы тем выше, чем сильнее свойства целого отличаются от простой суммы свойств его частей, и подчеркивал роль моделирования и математики как потенциальных методов решения задач тектологии. Он довел построения тектологии до рассмотрения проблемы кризисов, т.е. таких моментов в истории системы, когда неизбежна скачкообразная перестройка ее структуры.

Тот факт, что тектологией заинтересовались лишь в середине XX в., объясняется во многом сложностью судьбы Богданова. Будучи по образованию медиком, он всерьез заинтересовался философией и создал собственную философскую концепцию -эмпириомонизм. В.И. Ленин в своей книге «Материализм и эмпириокритицизм» подверг его жесткой критике, после чего Богданов отошел от философии. В 1926 г. он создал первый в мире Институт переливания крови и стал его директором. Там он начал проверять некоторые выводы тектологии на примере кровеносной системы. Рискованные опыты по переливанию крови он проводил на себе, а один из опытов в 1928 г. закончился его гибелью.

Массовое усвоение системных понятий, осознание системности мира, общества и человеческой деятельности началось в 1948 г., когда американский математик Н. Винер опубликовал книгу «Кибернетика» [9]. Первоначально он определил кибернетику как «науку об управлении и связи в животных и машинах». Однако уже в следующей своей книге Винер анализирует с позиций кибернетики процессы, происходящие в обществе. Научное сообщество отреагировало на появление кибернетики неоднозначно, полагая, что одна дисциплина не может рассматривать одновременно технические, биологические, экономические и социальные объекты и процессы. Первый международный конгресс по кибернетике (Париж, 1956) принял предложение считать кибернетику не наукой, а «искусством эффективного действия». В нашей стране кибернетика была встречена особенно настороженно и даже враждебно. Однако по мере ее развития стало ясно, что кибернетика - это самостоятельная наука со своим предметом изучения и своими методами исследования. Так, по А.И. Бергу, кибернетика - это наука об оптимальном управлении сложными динамическими системами; по А.Н. Колмогорову, кибернетика - это наука о системах, воспринимающих, хранящих, перерабатывающих и использующих информацию. Эти определения признаны достаточно общими и полными.

Уже из самих определений ясно, что предметом кибернетики является исследование сложных систем. Более того, хотя при изучении системы требуется учет ее конкретных свойств, для кибернетики в принципе несущественно, какова природа этой системы, т.е. является ли она физической, биологической, экономической, организационной или даже воображаемой. В поле зрения кибернетики попадают объекты любой природы, как только выясняется, что это сложные системы. То, что методы кибернетики могут применяться при исследовании объектов, традиционно изучаемых другими науками, можно трактовать как рассмотрение этих объектов с другой точки зрения. Более того, при этом происходит взаимное обогащение: кибернетика получает возможность развивать и совершенствовать свои модели и методы, а кибернетический подход к системе определенной природы позволяет прояснить некоторые проблемы данной науки, выдвинуть перед ней новые проблемы, а главное — содействовать повышению ее системности.

С кибернетикой Винера связаны такие достижения в развитии системных представлений, как типизация моделей систем, выявление особого значения обратных связей в системе и принципа оптимальности в управлении и синтезе систем, осознание информации как всеобщего свойства материи и возможности ее количественного описания, развитие методологии моделирования вообще и в особенности идеи математического эксперимента с помощью компьютера.

Параллельно и в определенной степени независимо от кибернетики развивается еще один подход к науке о системах - общая теория систем. В естествознании осознанная системность часто развивается именно на основе этого подхода. Идея построения теории, которая может быть использована в изучении систем любой природы, была выдвинута австрийским биологом Л. фон Берталанфи, опубликовавшим свои соображения в книге «Общая теория систем» в 1968 г. Один из путей реализации этой идеи он видел в том, чтобы отыскивать структурное сходство законов, установленных в различных дисциплинах, и, обобщая их, выводить общесистемные закономерности [4].

Важным достижением Берталанфи является введение понятия открытой системы. В отличие от винеровского подхода, где изучаются внутрисистемные обратные связи, а функционирование систем рассматривается как отклик на внешние воздействия, Берталанфи указал на особое значение обмена системы веществом, энергией и информацией (негэнтропией) с окружающей средой. В открытой системе устанавливается динамическое равновесие, которое может быть направлено в сторону усложнения организации (вопреки второму закону термодинамики, благодаря вводу негэнтропии извне), и функционирование является не просто откликом на изменение внешних условий, а сохранением старого или установлением нового подвижного внутреннего равновесия системы. Берталанфи и его последователи пытались придать общей теории систем формальный характер, но замысел построить общую теорию систем как новую логико-математическую дисциплину до сих пор не реализован полностью. Большую ценность общей теории систем имеет не столько ее математическое оформление, сколько разработка целей и задач системных исследований, развитие методологии анализа систем, установление общесистемных закономерностей.

Прогресс в области системности в исследовании систем связан с бельгийской школой во главе с И. Пригожиным. Развивая термодинамику неравновесных физических систем, он понял, что обнаруженные им закономерности характерны для систем любой природы [23]. Наряду с переоткрытием уже известных положений (иерархичность уровней организации систем; несводимость друг к другу и невыводимость друг из друга закономерностей разных уровней организации; наличие наряду с детерминированными случайных процессов на каждом Уровне организации и др.) Пригожий предложил новую теорию системодинамики. Согласно его взглядам, материя не является пассивной субстанцией, ей присуща спонтанная активность, вызванная неустойчивостью неравновесных состояний, в которые рано или поздно приходит любая система в результате взаимодействия с окружающей средой. Важно, что в такие переломные моменты (особые точки, или точки бифуркации) принципиально невозможно предсказать, станет ли система менее организованной или более организованной (диссипативной, в терминологии Пригожина). После опубликования в 1978 г. (на русском - в 1980 г.) работы Г. Хакена «Синергетика» направление, занимающееся изучением сложных саморазвивающихся систем, стало называться синергетикой [31]. По Хакену, в рамках синергетики анализируется совместное действие отдельных частей неупорядоченной системы, результатом которого является самоорганизация системы.

Таким образом, наращивание системности знаний - постоянный процесс, происходящий во всех областях человеческой деятельности. Осознанное использование системного подхода к изучению различных объектов и явлений, в том числе природных, в настоящее время развивается в рамках трех основных направлений — кибернетики, общей теории систем и синергетики. Попытки объединить все эти направления предпринимаются системным анализом. Обращаем внимание на специально ста ученых, стоявших в основании осознанной системности: Б. Трентовский - философ, Е.С. Федоров - геолог, A.A. Богданов — медик, H. Винер — математик, Л. фон Берталанфи - биолог, И. Пригожин — физик; уже это говорит о всеобщности проблем системности.

§ 4.2. Модели и моделирование систем

Понятие модели и моделирования

Одна из характерных особенностей современного естествознания — его модельный характер, т.е. все объекты, явления и процессы описываются с помощью моделей. В определенном смысле расширение границ естествознания можно представить как построение более подходящих и совершенных моделей природы. Модельный характер естествознания связан и с тем, что значимость того или иного факта можно определить, лишь опираясь на какую-либо модель.

Понятие модели стало пониматься широко лишь в XX в. Вначале модель стала осознаваться как нечто универсальное в научных дисциплинах информационного, кибернетического, системного направлений, а позднее эта идея распространилась на всю науку. При этом понятие абстрактной модели не сводится к математическим моделям, а относится к любым знаниям и представлениям о мире [18, 20, 22, 30, 33].

Под моделью будем понимать вещественный или мысленно представляемый аналог определенного оригинала, подобный ему в существенных для конкретного исследования чертах. По сути модель является неким «заместителем» оригинала в познании и практике. Основные функции моделей - фиксация знаний и получение информации. Они служат для хранения и расширения знания или, как иногда говорят, информации об оригинале, конструирования оригинала, преобразования и управления им.

Моделированием называется исследование каких-либо явлений, процессов или систем путем построения и изучения их моделей, а также использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов.

Моделирование - одна из основных категорий теории познания. На идее моделирования по существу базируется любой метод научного исследования.

Моделирование является важным этапом целенаправленной деятельности, так как она ориентирована на реализацию образа желаемого будущего, т.е. модели состояния. Например, земледелец возделывает почву для того, чтобы произвести продукты питания; студент учится для того, чтобы приобрести профессию; ученые изучают природу для того, чтобы получить знания об окружающем мире. Любая деятельность осуществляется по определенному плану (алгоритму), который является образом будущей деятельности, т.е. ее моделью. При этом приходится оценивать текущий результат предыдущих действий и выбирать следующий шаг из многих возможных, в связи с чем необходимо сравнивать последствия всех возможных шагов, не выполняя их реально, другими словами, изучать их на модели. Кроме того, сама модель является целевым отображением, причем не самого по себе объекта-оригинала, а того, что в нем нас интересует, т.е. то, что соответствует поставленной цели. Поскольку модель - это целевое отображение, можно говорить о множественности моделей одного и того же объекта: для разных целей, как правило, требуются разные модели.

Классификация моделей

В зависимости от направленности моделирования (теоретическая или практическая) модели можно разделить на познавательные и прагматические [22]. Познавательные модели являются формой организации и представления знаний, средством соединения новых знаний с имеющимися. Поэтому при обнаружении расхождения между моделью и реальностью встает задача устранения этого расхождения путем изменения модели, так как познавательная деятельность ориентирована в основном на приближение модели к реальности, которую модель отображает. Примером здесь могут служить все усложняющиеся модели пространства и времени в естествознании.

Прагматические модели являются средством управления и средством организации практических действий, способом представления образцовых действий или их результата. При их использовании в случае обнаружения расхождений между моделью и реальностью усилия направляют на изменение реальности так, чтобы приблизить реальность к модели. Прагматические модели носят нормативный характер, выполняя функцию стандарта, образца, под которые «подгоняются» деятельность и ее результаты. Прагматические модели - это планы, алгоритмы и программы действий (например, по преобразованию ландшафта какой-либо территории) и т.д. Следовательно, познавательные модели стремятся отражать существующее, а прагматические - желаемое.

Модели также можно разделить на статические - модели конкретного состояния интересующего нас объекта - и динамические — когда возникает необходимость в отображении процесса изменений состояния. Например, в одних случаях нужны модели некоторого ландшафта в некоторый момент времени, а в других - модель сезонной смены его состояний; можно описать структуру кристалла алмаза, а можно рассмотреть процесс его формирования; можно характеризовать анатомию человеческого организма или построить модель его функционирования или развития.

Наибольшее распространение получила классификация моделей на абстрактные (мысленные, идеальные) и материальные (реальные, вещественные) в зависимости от способа их воплощения или реализации или на основании использования того или иного способа передачи информации, поскольку в распоряжении человека, создающего модель, имеются средства самого сознания и средства окружающего материального мира [30, 33].

Абстрактные, модели — идеальные конструкции, построенные средствами мышления, сознания. Для человеческого мозга важную роль играют неязыковые формы мышления: эмоции, бессознательное, интуиция, озарение, образное мышление, подсознание и т.п. К абстрактным моделям относятся лингвистические конструкции - продукт мышления, готовый или почти готовый для передачи другим носителям языка. Естественные языки являются универсальным средством построения абстрактных моделей, поскольку на них можно говорить практически обо всем, и, кроме того, языковые модели обладают неоднозначностью. Многозначность слов (например, «мало», «много», «несколько») наряду с многовариантностью их возможных соединений во фразы позволяет отобразить любую ситуацию с достаточной для обычных практических целей точностью. Для ситуаций, когда приблизительность естественного языка становится недостатком, вырабатывается специфический язык. Например, у северных народов имеется несколько десятков разных слов, обозначающих снег в различных состояниях; языковые модели различных естественно-научных отраслей более точны и содержат больше информации, чем естественные языки. Новые знания аккумулируются в новых моделях, и если старых языковых средств для их построения не хватает, то возникают еще более специализированные языки. Одним из специальных и достаточно универсальных языков науки является математика.

В общем случае мысленные модели, используемые в естествознании, можно разделить на образные, образно-знаковые и знаковые модели. К образным моделям относятся неформализованные мысленные представления, гипотетические построения, разного рода мод ели-аналогии и прочие модельные представления; например, утверждая, что Земля похожа на шар, мы выстраиваем образную модель; в более сложном виде — это словесное описание некоторой гипотезы, теории, концепции или парадигмы. Образно-знаковые модели - разного рода схемы, графы, чертежи, графики - широко распространены в естествознании; так, в науках о Земле и астрономии большое значение имеет такой вид образно-знаковых моделей, как карты. Знаковыми моделями называют определенным образом интерпретированные системы. Наиболее важны в этой группе математические модели.

Материальные (реальные, вещественные) модели - некоторая материальная конструкция. Чтобы она могла быть отображением, т.е. замещала в каком-то отношении оригинал, между оригиналом и моделью должно быть установлено отношение схожести, подобия. В рамках материальных моделей по характеру подобия выделяют модели, построенные на принципе прямого и косвенного подобия; иногда выделяют модели условного подобия.

К построенным на основе прямого подобия относят пространственно и физически подобные модели. Пространственно подобные модели геометрически подобны оригиналу. Языком пространственно подобных моделей передаются наиболее общие черты формы объекта и соотношения определенных его частей. Например, фотографии, макет рельефа местности, масштабированные модели самолетов или гидротехнических сооружений, макеты зданий, шаблоны и т.п. Физически подобные модели обладают механическим, динамическим, кинематическим и другими видами подобия с оригиналом. Эти модели широко применяются во многих отраслях естествознания. Так, с их помощью изучают на небольших лабораторных установках деформации, происходящие в земной коре, формирование долин крупных рек, влияние еще не построенных гидроэлектростанций на окружающую среду и т.д.

Прямое подобие (геометрически и физически подобные модели) связано с проблемой переноса результатов моделирования на оригинал. Например, при изучении поведения русла реки на уменьшенной модели часть условий эксперимента можно привести в соответствие с натурой, изменяя масштабы модели (скорость течения, глубина потока, морфология русла), а часть условий (вязкость и плотность воды, сила тяготения, определяющие свойства волн, и т.д.) не может быть масштабирована. Задачами пересчета данных модельного эксперимента на реальные условия занимается теория подобия, которая позволяет перейти с использованием коэффициентов подобия от оригинала к модели и наоборот.

Косвенное подобие между оригиналом и моделью — аналогия — проявляется в совпадении или достаточной близости их абстрактных моделей и используется в практике реального моделирования. Наиболее известна электромеханическая аналогия, основанная на том, что некоторые закономерности электрических и механических процессов описываются одинаковыми дифференциальными уравнениями, различающимися лишь физической интерпретацией переменных, входящих в эти уравнения. Поэтому можно не только заменить неудобное и громоздкое экспериментирование с механической конструкцией на простые опыты с электрической схемой, перепробовать множество вариантов, не переделывая конструкцию, но и проверить на модели варианты, в механике пока не осуществимые (например, с произвольным и непрерывным изменением масс, длин и т.д.). Роль моделей, обладающих косвенным подобием оригиналу, очень велика. Например, часы являются аналогом времени; подопытные животные у медиков - аналоги человеческого организма; автопилот — аналог летчика; электрический ток в подходящих цепях может моделировать течение воды в водоносном горизонте или в русле реки, а также транспортные потоки, перенос информации в сетях связи и т.д.

Модели условного подобия основаны на том, что подобие оригиналу устанавливается в результате соглашения. К ним причисляют различные географические карты и планы (модели местности), рабочие чертежи (модели будущей продукции), разнообразные сигналы (модели сообщений), деньги (модель стоимости), удостоверения личности (официальная модель владельца) и т.д. Данные модели являются вещественной формой, в которой абстрактные модели могут передаваться от одного человека к другому, храниться до момента их использования на основе соглашения о том, какое именно состояние реального объекта ставится в соответствие конкретной абстрактной модели. Обычно эти соглашения формулируются в виде совокупности правил построения моделей условного подобия и правил пользования ими. (Заметим, что выше эти модели мы определяли как мысленные образно-знаковые. Это подчеркивает условность рассматриваемой классификации, а также широту охвата и многоплановость модельных представлений.)

Особенности моделей

Для того чтобы модель отвечала своему назначению, необходимо существование условий, обеспечивающих ее функционирование. Так, географическую карту можно понять, только зная значения тех условных обозначений, которые на нее нанесены; древнеегипетская клинопись не могла быть прочитана, пока не был найден камень, на котором текст был изображен и на забытом древнеегипетском языке, и на древнегреческом. Следовательно, для реализации своих модельных функций модель должна быть согласована со средой, в которой ей предстоит функционировать.

Главными различиями между моделью и действительностью являются конечность, упрощенность и приближенность модели [22]. Так, реальный мир бесконечен в своих проявлениях и связях. Однако бесконечный мир необходимо познавать конечными средствами, имеющимися в распоряжении человека. Это возможно именно в результате построения моделей. Так, А. Розенблют и Н. Винер отмечали, что частные модели являются единственным средством, выработанным наукой для понимания мира. Конечность мысленных моделей выражается в том, что они наделяются строго фиксированным количеством свойств. В вещественных моделях из множества свойств объекта-модели выбираются и используются лишь некоторые свойства, подобные свойствам объекта-оригинала.

Конечность моделей делает неизбежными их упрощенность и приближенность. Как правило, для достижения цели оказывается вполне достаточным неполное, упрощенное отображение действительности. Степень упрощения зависит от целей моделирования. Упрощение является важным средством для выявления главных эффектов в исследуемом явлении. Это видно на примере таких моделей, как идеальный газ, непоглощающее зеркало, абсолютно черное тело, математический маятник и т.д. Уровень упрощения обусловливается также возможностью оперирования с моделями. Так, одно дело проводить моделирование с использованием логарифмической линейки, а другое — с помощью компьютера. Более того, давно замечено, что из двух моделей, с одинаковой точностью описывающих некоторое явление, более простая будет и более успешной. Например, геоцентрическая модель Птолемея позволяла с достаточной точностью рассчитать движения планет, предсказать затмения Солнца, но требовала расчетов по очень громоздким формулам с переплетением многочисленных «циклов». На смену геоцентрической системе пришла более простая и изящная гелиоцентрическая система Н. Коперника.

Приближенность моделей в отображении действительности также является неотъемлемым свойством модели. Так, абсолютно точной картой страны будет только сама эта страна, а абсолютно точной моделью атома может быть сам атом. Приемлемое различие определяется целью моделирования. Так, точность наручных часов обычно достаточна для повседневных целей и недостаточна для многих других целей, в том числе научных.

Модель, с помощью которой достигается поставленная цель, должна быть адекватна этой цели, т.е. требования полноты, точности и истинности должны выполняться не вообще, а лишь в той мере, которая достаточна для достижения цели. Например, геоцентрическая модель Птолемея была адекватной в смысле точности описания движения планет и не лишена истинности: относительно Земли Солнце и планеты действительно движутся; шаман, объясняющий свое успешное врачевание силами духов, предлагает адекватную, но ложную модель. В ряде случаев удается ввести меру адекватности модели, т.е. указать способ сравнения моделей по степени успешности достижения цели с их помощью. В таких случаях говорят об идентификации модели (о нахождении в заданном классе моделей наиболее адекватной), об исследовании чувствительности и устойчивости моделей (о зависимости меры адекватности модели от ее точности), об адаптации моделей (подстройке параметров модели с целью повышения адекватности) и т.п.

Заметим, что об истинности, правильности или ложности модели самой по себе говорить бессмысленно. Степень истинности выявляется лишь в практическом соотнесении модели с отображаемой ею натурой, причем изменение условий, в которых ведется сравнение, весьма значимо влияет на его результат и может привести к существованию двух противоречивых, но одинаково истинных моделей одного объекта. Примером этого могут являться волновая и корпускулярная модели света или электрона; эти модели различны, противоположны и истинны, но каждая в своих условиях.

Любая модель явно или неявно содержит условия своей истинности, и одна из опасностей практики моделирования состоит в применении модели без проверки выполнения этих условий. Например, при обработке экспериментальных данных часто употребляют статистические процедуры, не проверяя условий их применимости (скажем, нормальности или независимости). Когда это делается вынужденно (не всякое условие возможно проверить), к полученным результатам должно быть осторожное, условное отношение. Такие ситуации выдвинули перед исследователями проблему создания моделей, применимость которых сохраняется в некотором диапазоне условий.

Основные типы моделей систем

При изучении систем используют модели «черного», «белого» и «серого» ящика. Систему представляют как «черный ящик», если неизвестно внутреннее строение самой системы; ее поведение и функционирование изучается по входному и выходному сигналам. При изучении системы как «белого ящика», наоборот, известны все элементы и их взаимосвязи. Систему рассматривают как «серый ящик», когда что-то из внутреннего строения объекта известно, а что-то остается неизвестным, например модель состава системы с неизвестной структурой или, наоборот, модель структуры с неизвестным составом.

В рамках модели «черного ящика» внутреннее устройство системы изображают в виде непрозрачного ящика, выделенного из окружающей среды (рис. 4.1). Эта модель отражает два важных свойства системы — целостность и обособленность от среды [22]. Система не является полностью изолированной от среды, она связана со средой и с помощью этих связей взаимодействует с ней (входы и выходы системы). В модели «черного ящика» отсутствуют сведения о внутреннем содержании системы, а задаются, фиксируются и перечисляются только входные и выходные связи системы со средой. В одних случаях достаточно содержательного словесного описания входов и выходов; тогда модель «черного ящика» является просто их списком. В других случаях требуется количественное описание некоторых или всех входов и выходов с заданием двух множеств Х и У входных и выходных переменных.

Модель «черного ящика» в ряде случаев является единственно применимой при изучении систем. Например, при исследовании психики человека или влияния лекарства на живой организм ученый лишен возможности вмешательства в систему иначе, как только через ее входы, и делает выводы лишь на основании наблюдения за ее выходами. Часто приходится ограничиваться моделью «черного ящика» в связи с отсутствием данных о внутреннем устройстве системы. Например, мы не знаем, как «устроен» электрон, но знаем, как он взаимодействует с электрическими и магнитными полями, с гравитационным полем. Это и есть описание электрона на уровне модели «черного ящика».

Для решения вопросов, касающихся внутреннего устройства системы, недостаточно только модели «черного ящика» — необходимы более развитые модели. Например, любая система внутренне неоднородна, что позволяет различать составные части самой системы, причем некоторые части системы в свою очередь могут быть разбиты на составные части и т.д. Части системы, которые рассматриваются как неделимые, называют элементами, а части системы, состоящие более чем из одного элемента, — подсистемами. В результате получается модель состава системы, которая описывает, из каких подсистем и элементов состоит система (рис. 4.2) [22].

Для того чтобы составить представление о свойствах изучаемого объекта, часто бывает необходимо выявить определенные связи (отношения) между элементами. Совокупность связей элементов друг с другом, обеспечивающих целостность системы, называют ее структурой. Модель структуры в простейшем виде представляет собой список существенных для решения конкретной задачи отношений. Так, при расчете механизма не учитываются силы взаимного притяжения его деталей, хотя, согласно закону всемирного тяготения, такие силы объективно существуют; в то же время вес деталей (т.е. сила их притяжения к Земле) учитывается обязательно.

Поскольку все структурные схемы имеют много общего, возможно абстрагирование от их содержательной стороны и соответственно построение схем, в которых обозначены только элементы и связи между ними, а также (в случае необходимости) разница между элементами и между связями. Такая схема называется графом.

Граф (рис. 4.3) состоит из обозначений элементов произвольной природы - вершин и обозначений связей между ними - ребер (дуг). Если необходимо отразить несимметричность некоторых связей, линию, изображающую ребро, снабжают стрелкой. Если направления связей не обозначаются, граф называют неориентированным, при наличии стрелок - ориентированным (полностью или частично). Любая пара вершин может быть соединена с любым количеством ребер; вершина может быть соединена сама с собой (тогда ребро называют петлей). Если в графе требуется отразить другие различия между элементами или связями, то либо приписывают разным ребрам различные веса (взвешенные графы), либо раскрашивают вершины или ребра (раскрашенные графы) [2, 21].

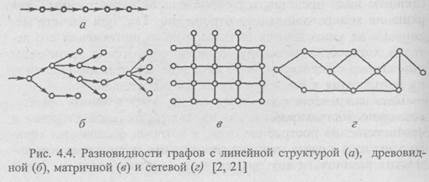
Графы могут изображать любые структуры, в том числе в различных областях естествознания. Так, при анализе природных систем часто используют линейные, древовидные (иерархические), матричные и сетевые структуры (рис. 4.4).

Например, в виде древовидного графа можно изобразить речной бассейн и изучать соотношение притоков и главного русла.

Если соединить модели «черного ящика», состава и структуры, то образуется модель, которую часто называют «белый (прозрачный) ящик» (рис. 4.5). В «белом ящике» указываются все элементы системы, все связи между элементами внутри системы и связи определенных элементов с окружающей средой (входы и выходы системы). Такие модели часто называют структурными схемами системы [22].

Если при исследовании системы не учитываются ее изменения во времени, то модель называется статической. Чтобы понять и описать, как система работает (функционирует) и что происходит с ней самой и с окружающей средой в ходе ее развития, нужны такие модели, которые отражают поведение систем, описывают происходящие с течением времени изменения, последовательность этапов, операций, действий, причинно-следственные связи. Модели, отображающие изменения в системах в течение времени, называются динамическими.

Разработано большое количество динамических моделей, описывающих процессы с различной степенью детальности: от самого общего понятия динамики, движения вообще, до формальных математических моделей конкретных процессов типа уравнений движения в механике или волновых уравнений в теории поля.

Обычно говорят о двух типах динамики системы: функционировании, т.е. устойчивой последовательности постоянно действующих процессов в системах, обеспечивающей сохранение того или иного характерного для значительного отрезка времени состояния этой системы, и развитии — необратимом, направленном, закономерном изменении системы, которое может привести к смене структуры системы. Типы динамических моделей такие же, как и статических, но элементы этих моделей имеют временной характер. Так, динамический вариант «черного ящика» содержит указания о начальном («вход») и конечном («выход») состояниях системы; модели состава соответствует перечень этапов в некоторой упорядоченной последовательности действий; динамический вариант «белого ящика» - подробное описание происходящего или планируемого процесса.

§ 4.3. Системные исследования

Информационные аспекты изучения систем

Информация — специфическая форма взаимодействия между объектами любой физической природы или, точнее, такой аспект взаимодействия, который несет сведения о взаимодействующих объектах. В сущности информация - мера организованности системы в противоположность понятию энтропии как меры неорганизованности [6, 7, 22, 24, 32].

Представление об энтропии как мере неорганизованности было введено Р. Клаузиусом в связи с изучением термодинамических явлений. Л. Больцман дал статистическую интерпретацию энтропии, позволившую рассматривать энтропию как меру вероятности пребывания системы в конкретном состоянии. Больцман показал, что природные процессы стремятся перевести термодинамическую систему из состояний менее вероятных в состояния более вероятные, т.е. привести систему в равновесное состояние, для которого значения энтропии (неупорядоченности) максимальны. После построения в середине XX в. К.Э. Шенноном теории информации оказалось, что формула Больцмана для термодинамической энтропии и формула Шеннона для информационной энтропии тождественны [32]. Таким образом, понятие энтропии приобрело более универсальный смысл в изучении систем различного происхождения.

Изучение потоков информации в системах имеет очень большое значение. Так, если вещественные и энергетические потоки обеспечивают целостность системы и возможность ее существования, то потоки информации, переносимые сигналами, организуют все ее функционирование, управляют ею. Поэтому при изучении любого объекта как системы не следует ограничиваться рассмотрением и описанием вещественной и энергетической его сторон, необходимо проводить исследование информационных аспектов системы (сигналов, информационных потоков, организации, управления и т.д.).

Информационный анализ систем использует представление о сигналах - носителях информации, средстве перенесения информации в пространстве и времени. В качестве сигналов выступают состояния некоторых объектов: чтобы два объекта содержали информацию друг о друге, необходимо соответствие между их состояниями; тогда по состоянию одного объекта можно судить о состоянии другого. Соответствие между состояниями двух объектов устанавливается либо в результате непосредственного взаимодействия, либо с помощью взаимодействия с промежуточными объектами. Например, от преподавателя до ушей студентов звук переносят колебания воздуха.

Не всякое состояние имеет сигнальные свойства, поскольку объект взаимодействует не только с тем объектом, информацию о котором требуется получить, но и с другими объектами, в результате чего соответствие состояний ослабевает. Условия, обеспечивающие установление и способствующие сохранению сигнального соответствия состояний, называют кодом, а посторонние воздействия, нарушающие это соответствие, - помехами или шумами. Нарушение соответствия состояний возможно не только вследствие помех, но и из-за рассогласования кодов взаимодействующих объектов. При этом предполагается, что в природных системах согласование кодов происходит в самой структуре систем путем естественного отбора различных вариантов.

Сигналы делятся на два типа:

1) статические сигналы, являющиеся стабильными состояниями физических объектов (например, книга, фотография, магнитофонная запись, состояние памяти компьютера, положение триангуляционной вышки и т.д.);

2) динамические сигналы, в качестве которых могут выступать динамические состояния силовых полей. Изменение состояния таких полей приводит к распространению возмущения, конфигурация которого во время распространения обладает определенной устойчивостью, что обеспечивает сохранение сигнальных свойств. Примерами таких сигналов могут служить звуки (изменение состояния поля сил упругости в газе, жидкости или твердом теле), световые и радиосигналы (изменения состояния электромагнитного поля). Так как сигналы - это состояния физических объектов, можно математически описать данное явление. Например, можно зафиксировать звуковые колебания, соответствующие конкретному сигналу, в виде зависимости давления х от времени t и изобразить этот сигнал функцией х (t). Так же функцией можно изобразить и статический сигнал, например запись звука на магнитной ленте, поставив в соответствие параметру t протяженность (длину) записи. Однако между просто состоянием объекта и сигналом имеется существенное различие: единственная функция x(t) не исчерпывает всех важных свойств сигналов. Дело в том, что понятие функции предполагает, что нам известно значение х (либо правило его вычисления) для каждого интервала времени. Но если это известно получателю сигнала, то отпадает необходимость в его передаче, так как функция x(t) может быть и без этого воспроизведена на приемном конце. Следовательно, функция приобретает сигнальные свойства только тогда, когда она является одной из возможных функций. Моделью сигнала может быть набор (ансамбль) функций параметра t, причем до передачи сигнала неизвестно, какая из них будет отправлена. Каждая такая конкретная функция называется реализацией. Если ввести вероятностную меру на множество реализации, то получается математическая модель, называемая случайным процессом.

Специфическим для теории информации является понятие неопределенности случайного объекта, для которой и была введена количественная мера — энтропия. Пусть, например, некоторое событие может произойти с вероятностью 0,99 (99%) и не произойти с вероятностью 0,01 (1%), а другое событие имеет вероятности соответственно 0,5 (50%) и 0,5 (50%). В первом случае результатом опыта «почти наверняка» является наступление события, а во втором неопределенность исхода так велика, что от прогноза разумнее воздержаться.

В качестве меры неопределенности случайного объекта А с конечным множеством возможных состояний А₁,..., А_n соответствующими вероятностями р_1,..., р_n принимают величину

которую называют энтропией случайного объекта А (или распределения вероятностей {p_i}) и используют в качестве меры неопределенности. Обобщение этой меры на непрерывные случайные величины выглядит следующим образом:

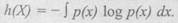
Функция h(X) получила название дифференциальной энтропии и является аналогом энтропии дискретной (прерывной) величины.

Это позволяет интерпретировать процесс получения информации как изменение неопределенности в результате приема сигнала. Тогда количество информации можно представить как меру снятой неопределенности: числовое значение количества информации о некотором объекте равно разности априорной и апостериорной энтропии этого объекта, иначе говоря, как меру уменьшения неопределенности в результате получения сигнала. При этом в результате обработки уже полученных данных содержащееся в них количество информации не может быть увеличено. Следовательно, обработка делается лишь для представления информации в более удобном, компактном виде и в лучшем случае без потери полезной информации.

Информация и энтропия - безразмерные величины. За единицу энтропии принимают неопределенность случайного объекта, такого, что

т.е. энтропия (неупорядоченность) равна единице (достигает максимального значения) при данном т, когда все исходы равновероятны, и равна нулю в том случае, когда одна из p_i равна единице, а остальные равны нулю, т.е. когда исход опыта достоверен. Следует конкретизировать число т состояний объекта и основание логарифма. Наименьшее число возможных состояний, при котором объект остается случайным, равняется 2 (т = 2). Если в качестве основания логарифма также взять число 2, то единицей неопределенности служит энтропия объекта с двумя равновероятными состояниями — бит. Например, количество информации 1 бит дает бросание монеты. Для непрерывных величин обычно употребляется другая единица (нит), которая получается при использовании натурального логарифма.

При обмене информацией между системами возникают специфические эффекты, полезные для анализа систем. Например, избыточность - явление не всегда отрицательное. При искажениях, выпадениях и вставках символов именно избыточность позволяет обнаружить и исправить ошибки.

Важным понятием информационного характера является скорость передачи информации - количество информации, передаваемое в единицу времени. В дискретном случае единицей времени удобно считать время передачи одного символа. Для непрерывных каналов единицей времени может служить либо обычная единица (например, секунда), либо интервал между отсчетами. Для более наглядного представления об этой величине укажем, что темп обычной речи человека соответствует скорости примерно 20 бит/с, муравьи обмениваются информацией (путем касания усиками) со скоростью около 0,1 бит/с. Скорость передачи информации по каналу связи зависит от многих факторов (энергия сигнала, количество символов в алфавите, избыточность, способ кодирования и декодирования и т.д.) и не превышает некоторого предела, называемого пропускной способностью канала. Например, пропускные способности зрительного, слухового и тактильного (осязательного) каналов связи человека составляют приблизительно 50 бит/с (заметим, что распространено мнение о сильном отличии зрительного канала). Если включить в канал и «исполнительные» органы человека (например, предложить ему нажимать педаль или кнопку в темпе получения сигналов), то пропускная способность снизится до 10 бит/с.

Теория информации имеет большое значение для системного подхода. Ее конкретные методы и результаты позволяют проводить количественные исследования информационных потоков в изучаемой системе. Однако более важным является эвристическое значение основных понятий теории информации - неопределенности, энтропии, количества информации, избыточности, пропускной способности и др.

Этапы системного исследования

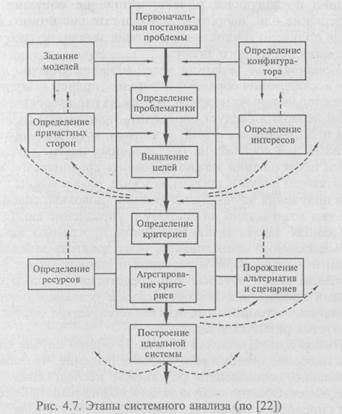
Любое системное исследование имеет определенную структуру и проводится по определенному алгоритму. Так, для целей экологии Дж. Джефферс рекомендует алгоритм, показанный на рис. 4.6 и включающий следующие этапы системного анализа: выбор проблемы, постановку задачи и ограничение степени ее сложности, установление иерархии целей и задач, выбор путей решения, моделирование, оценку возможных стратегий и, наконец, внедрение результатов [10].Ф.И. Перегудов и Ф.П. Тарасенко предлагают другой алгоритм постановки задач системного исследования, изображенный на рис. 4.7, где помимо опорной последовательности действий (утолщенные сплошные линии) предусматривается возможность возврата к уже выполненным действиям в случае необходимости (штриховые линии) [22].

Однако системный анализ, а тем более системный подход не предполагает строго определенного набора рецептов. Поэтому, говоря о некоторых этапах и направлении системной деятельности, следует рассматривать их только как руководство к действию. При решении конкретных задач часть этапов может быть исключена или изменен порядок их следования. Иногда приходится повторять эти этапы в различном порядке. Например, если необходимо уточнить роль исключенных на первых этапах из рассмотрения факторов, требуется пройти несколько раз этапы моделирования и оценки возможных стратегий; для проверки адекватности целевой структуры исследования придется время от времени возвращаться к одному из ранних этапов даже после выполнения значительной части работы на более поздних этапах анализа и т.д.

Рассмотрим специфику системного исследования в естествознании на примере алгоритма Дж. Джефферса (см. рис. 4.6) [10].

1. Выбор проблемы. Выбор некой проблемы, которую можно исследовать только с помощью системного анализа, не всегда оказывается тривиальным шагом, но всегда столь же важен, как и правильный выбор метода исследования. Ведь можно взяться за решение проблемы, не поддающейся системному анализу, либо выбрать проблему, которая не требует для своего решения всей мощи системного анализа и изучать которую данным методом неэкономично.

2. Постановка задачи и ограничение степени ее сложности. Этот этап связан с упрощением задачи в той мере, чтобы она могла иметь аналитическое решение и в то же время сохранить все те элементы, которые делают проблему интересной для изучения. Успех или неудача исследования во многом зависит от умения выбрать равновесие между упрощением и усложнением, при котором сохранены все связи с исходной проблемой, достаточные для того, чтобы аналитическое решение поддавалось интерпретации. Может оказаться, что проект не осуществлен из-за того, что принятый уровень сложности затруднил последующее моделирование, не позволил получить решение или, напротив, в результате системного исследования получено тривиальное решение задачи, не требующее применения системного анализа.

-

3. Установление иерархии целей и задач. Обычно цели и задачи исследования образуют иерархию, причем основные задачи последовательно подразделяются на ряд второстепенных. В такой иерархии следует определить приоритеты различных этапов и соотнести их с теми усилиями, которые необходимо приложить для достижения поставленных целей. Так, в прикладном исследовании можно присвоить сравнительно малый приоритет тем целям и задачам, которые, хотя и важны с точки зрения получения научной информации, довольно слабо влияют на вид воздействий на систему и управление ею. Однако, когда данная задача составляет часть программы какого-то фундаментального исследования, исследователь заведомо ограничен в выборе форм управления и концентрирует усилия на решении задач, которые непосредственно связаны с конкретными процессами. В любом случае условием успешного применения системного анализа является четкое определение приоритетов различных задач.

4. Выбор путей решения задачи. В общем случае следует искать наиболее общее аналитическое решение, что позволит максимально использовать результаты исследования аналогичных задач. Обычно любую задачу можно решать более чем одним способом и применять решение, подобное известному, следует при допущениях, справедливых для данного конкретного случая. Поэтому полезно разрабатывать несколько альтернативных решений и выбрать то из них, которое лучше подходит для данной задачи.

5. Моделирование. Приступая к этапу моделирования, необходимо помнить, что моделируемым процессам, а также механизмам обратной связи присуща внутренняя неопределенность, а это может значительно усложнить как понимание системы, так и ее управляемость. Кроме того, в самом процессе моделирования при выработке решения о подходящей стратегии нужно учитывать ряд правил.

Процесс моделирования структурирован, т.е. состоит из последовательности этапов. Этапы различаются качественно, конкретными целями и средствами и должны выполняться в определенной очередности. Например, при имитационном моделировании выделяют: формирование целей моделирования - построение абстрактной модели - создание имитационной реальной модели — ее исследование - обработку и интерпретацию результатов.

Однако на практике чаще всего не удается строго выдержать рекомендуемую последовательность действий. Более того, очевидно, что нельзя выработать какой-то единый, пригодный для всех случаев алгоритм моделирования, поскольку в процессе создания моделей кроме осознанных формализованных, технических и научных приемов значительное место занимает творческое, интуитивное начало.

6. Оценка возможных стратегий. На этапе оценки потенциальных стратегий, полученных на модели, исследуется чувствительность результатов к допущениям, сделанным при построении модели, поскольку правомерность этих допущений можно проверить лишь в процессе использования модели. Если окажется, что основные допущения некорректны, возможно, придется вернуться к этапу моделирования, но часто удается улучшить модель, незначительно модифицировав исходный вариант. Обычно также исследуют чувствительность модели к тем аспектам проблемы, которые были исключены из формального анализа на этапе, когда ставилась задача и ограничивалась степень ее сложности.

7. Внедрение результатов. Если исследование проводилось по описанной выше схеме, то шаги, которые необходимо предпринять для внедрения результатов, достаточно очевидны. Заметим, что на последнем этапе может выявиться неполнота исследования на тех или иных этапах и необходимость их пересмотра, т.е. понадобится повторить какие-то этапы.

В заключение еще раз заметим, что возможности системного подхода огромны, но предлагаемые для исследования естественно-научные проблемы не всегда требуют использования арсенала системного подхода. Этот подход не отменяет и не заменяет классические исторически сложившиеся методы изучения природы - он его дополняет и обогащает, определяя специфику современного естествознания.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Что такое системность и системный подход? Какие проблемы позволяет эффективно решать системный подход? Какие уровни системности труда вы знаете?

2. Дайте определение системы. Какие основные свойства систем вы знаете? Кратко поясните эти свойства.

3. Какие классификации систем вы знаете? Укажите основания этих классификаций.

4. Когда зародились и как развивались системные представления? Специалисты каких областей знаний являлись инициаторами внедрения системности в научное знание?

5. Какие три основных направления сложились в изучении системности? Кратко охарактеризуйте специфику каждого направления.

6. Что такое модель и моделирование? Дайте определения и рассмотрите значение модельных представлений в современном естествознании.

7. На каком основании и как подразделяются модели природных явлений? Приведите примеры моделей разных типов и дайте обоснование необходимости их использования в естествознании.

8. Какие особенности моделей вы знаете? Поясните сущность конечности, упрощенности и приближенности моделей. В чем заключается требование к полноте, точности и истинности моделей?

9. Какие типы моделей систем выделяют? Что такое модели «черного», «серого» и «белого» ящика? Охарактеризуйте их и поясните, зачем они нужны.

10. Какое значение имеет информация в системных исследованиях? Дайте определение информации.

11.Что такое энтропия в теории информации? Какое значение она имеет для передачи информации?

12.Какие этапы системного исследования можно выделить? Охарактеризуйте каждый этап.

ЛИТЕРАТУРА

1. Аверьянов А.Н. Системное познание мира. М, 1985.

2. Белов В.В., Воробьев Е.М., Шаталов В.E. Теория графов. М., 1976.

3. Березина Л.Ю. Графы и их применение. М., 1979.

4. Берталанфи Л. фон. История и статус общей теории систем // Системные исследования: Ежегодник. М., 1973.

5. Богданов A.A. Всеобщая организационная наука (тектология): В 3 т. М., 1905—1924.