 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Контрольная работа. Кафедра Высшая математика и физика
|
|
УНИВЕРСИТЕТА МАШИНОСТРОЕНИЯ
Кафедра Высшая математика и физика
КОНТРОЛЬНАЯ РАБОТА
по дисциплине Вычислительная математика
вариант 2
Выполнил:
Студент группы 230100
Мышкин Василий Геннадьевич
учебный шифр 613272
Проверила:
преподаватель Тихонова Л.В.
Чебоксары 2015
Задание 1
Отделите корни уравнения f(x) аналитически уточните два корня методом касательных и простых итераций с точностью ɛ=0.001
5) x3-x2-4x-5=0
Построим график функции:
| точки перегиба | ||
| x= | -2,119632981 | |
| x= | 0,786299648 | |
| x | f(x) | f’(x) |
| -2,5 | -8,6250 | 12,75 |
| -2,38 | -7,2013 | 10,9932 |
| -2,26 | -5,9832 | 9,3228 |
| -2,14 | -4,9603 | 7,7388 |
| -2,02 | -4,1224 | 6,2412 |
| -1,9 | -3,4590 | 4,83 |
| -1,78 | -2,9598 | 3,5052 |
| -1,66 | -2,6143 | 2,2668 |
| -1,54 | -2,4123 | 1,1148 |
| -1,42 | -2,3433 | 0,0492 |
| -1,3 | -2,3970 | -0,93 |
| -1,18 | -2,5630 | -1,8228 |
| -1,06 | -2,8310 | -2,6292 |
| -0,94 | -3,1906 | -3,3492 |
| -0,82 | -3,6314 | -3,9828 |
| -0,7 | -4,1430 | -4,53 |
| -0,58 | -4,7151 | -4,9908 |
| -0,46 | -5,3373 | -5,3652 |
| -0,34 | -5,9993 | -5,6532 |
| -0,22 | -6,6906 | -5,8548 |
| -0,1 | -7,4010 | -5,97 |
| 0,02 | -8,1200 | -5,9988 |
| 0,14 | -8,8373 | -5,9412 |
| 0,26 | -9,5424 | -5,7972 |
| 0,38 | -10,2251 | -5,5668 |
| 0,5 | -10,8750 | -5,25 |
| 0,62 | -11,4817 | -4,8468 |
| 0,74 | -12,0348 | -4,3572 |
| 0,86 | -12,5239 | -3,7812 |
| 0,98 | -12,9388 | -3,1188 |
| 1,1 | -13,2690 | -2,37 |
| 1,22 | -13,5042 | -1,5348 |
| 1,34 | -13,6339 | -0,6132 |
| 1,46 | -13,6479 | 0,3948 |
| 1,58 | -13,5357 | 1,4892 |
| 1,7 | -13,2870 | 2,67 |
| 1,82 | -12,8914 | 3,9372 |
| 1,94 | -12,3386 | 5,2908 |
| 2,06 | -11,6182 | 6,7308 |
| 2,18 | -10,7198 | 8,2572 |
| 2,3 | -9,6330 | 9,87 |
| 2,42 | -8,3475 | 11,5692 |
| 2,54 | -6,8529 | 13,3548 |
| 2,66 | -5,1389 | 15,2268 |
| 2,78 | -3,1950 | 17,1852 |
| 2,9 | -1,0110 | 19,23 |
| 3,02 | 1,4236 | 21,3612 |
| 3,14 | 4,1191 | 23,5788 |
| 3,26 | 7,0860 | 25,8828 |
| 3,38 | 10,3345 | 28,2732 |
| 3,5 | 13,8750 | 30,75 |
| 3,62 | 17,7179 | 33,3132 |
| 3,74 | 21,8736 | 35,9628 |
| 3,86 | 26,3525 | 38,6988 |
| 3,98 | 31,1648 | 41,5212 |
График функции f(x) и производной f’(x)

Аналитически х=2.9
Уточним с помощью численных методов:
1)Метод итераций


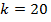
| k= | -20 | |
| x(n-1) | f(x(n-1)) | |
| 3,0000 | -0,0500 | -0,0276 |
| 2,9500 | 0,0014 | 0,0002 |
| 0,0005 |
Ответ: х1=2,9500
2) Метод касательных:
 xn= xn-1- f(xn-1)/f'(xn-1)
xn= xn-1- f(xn-1)/f'(xn-1)
| x(n-1) | f(x(n-1))/f'(x(n-1)) | f(x(n)) |
| 3,0000 | -0,0476 | 0,0203 |
| 2,9524 | -0,0010 | 0,0000 |
| 0,0005 |
Задание 2
2)


Приведём систему к диагональному преобладанию



| значения в системе при этих икс | 
| ||||||

| 
| 
| 
| 
| 
| 
| 
| 
|
| 0,0000 | 0,0000 | 0,0000 | -0,7000 | -1,1000 | -2,8000 | 0,7000 | 0,2200 | -0,0200 |
| 0,7000 | 0,2200 | -0,0200 | 1,0680 | 1,0820 | -0,2600 | 0,5384 | 0,0036 | -0,2280 |
| 0,5384 | 0,0036 | -0,2280 | -0,2078 | -0,3675 | -0,8412 | 0,7482 | 0,0771 | -0,2503 |
| 0,7482 | 0,0771 | -0,2503 | 0,3123 | 0,2829 | -0,1140 | 0,7086 | 0,0205 | -0,3245 |
| 0,7086 | 0,0205 | -0,3245 | -0,0546 | -0,1264 | -0,2809 | 0,7756 | 0,0458 | -0,3423 |
| 0,7756 | 0,0458 | -0,3423 | 0,0964 | 0,0684 | -0,0652 | 0,7694 | 0,0321 | -0,3728 |
| 0,7694 | 0,0321 | -0,3728 | -0,0104 | -0,0461 | -0,1078 | 0,7930 | 0,0414 | -0,3850 |
| 0,7930 | 0,0414 | -0,3850 | 0,0324 | 0,0130 | -0,0400 | 0,7946 | 0,0388 | -0,3993 |
| 0,7946 | 0,0388 | -0,3993 | 0,0006 | -0,0184 | -0,0478 | 0,8040 | 0,0424 | -0,4070 |
| 0,8040 | 0,0424 | -0,4070 | 0,0123 | 0,0000 | -0,0245 | 0,8064 | 0,0424 | -0,4144 |
| 0,8064 | 0,0424 | -0,4144 | 0,0024 | -0,0081 | -0,0238 | 0,8107 | 0,0440 | -0,4191 |
| 0,8107 | 0,0440 | -0,4191 | 0,0053 | -0,0021 | -0,0147 | 0,8126 | 0,0445 | -0,4231 |
| 0,8126 | 0,0445 | -0,4231 | 0,0020 | -0,0039 | -0,0127 | 0,8147 | 0,0453 | -0,4259 |
| 0,8147 | 0,0453 | -0,4259 | 0,0026 | -0,0018 | -0,0087 | 0,8160 | 0,0456 | -0,4281 |
| 0,8160 | 0,0456 | -0,4281 | 0,0014 | -0,0021 | -0,0071 | 0,8171 | 0,0460 | -0,4298 |
| 0,8171 | 0,0460 | -0,4298 | 0,0013 | -0,0012 | -0,0051 | 0,8179 | 0,0463 | -0,4311 |
| 0,8179 | 0,0463 | -0,4311 | 0,0009 | -0,0011 | -0,0040 | 0,8185 | 0,0465 | -0,4320 |
| 0,8185 | 0,0465 | -0,4320 | 0,0007 | -0,0008 | -0,0030 | 0,8190 | 0,0466 | -0,4328 |
| 0,8190 | 0,0466 | -0,4328 | 0,0005 | -0,0006 | -0,0023 | 0,8193 | 0,0468 | -0,4334 |
| 0,8193 | 0,0468 | -0,4334 | 0,0004 | -0,0005 | -0,0018 | 0,8196 | 0,0469 | -0,4338 |
| 0,8196 | 0,0469 | -0,4338 | 0,0003 | -0,0004 | -0,0013 | 0,8198 | 0,0469 | -0,4341 |
| 0,8198 | 0,0469 | -0,4341 | 0,0002 | -0,0003 | -0,0010 | 0,8199 | 0,0470 | -0,4344 |
| 0,8199 | 0,0470 | -0,4344 | 0,0002 | -0,0002 | -0,0008 | 0,8201 | 0,0470 | -0,4346 |

Задание 3
2) 



Для n=2

Подставив исходные данные, получим


Для n=3

Подставив исходные данные, получим


Для n=4

Подставив исходные данные, получим


Оценим погрешность

| 
| 
| |
| n=2 | 
| 2,5 | 0,5 |
| n=3 | 
| 0,3 | 1,7 |
| n=4 | 
| 2,4 | 0,4 |
Задание 4
Вычислите интеграл 
а) по формуле прямоугольников с точностью до 10-2
б) по формуле трапеций с точностью до 10-3
в) по формуле Симпсона с точностью до 10-4
1) 
Точное значение
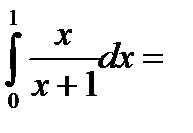


Дата публикования: 2015-10-09; Прочитано: 187 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
