Задания 11 – 20

Для решения задач 11 – 20 рекомендуется учебное пособие [5]

Гл. I –IV, стр.39 – 91.

В пирамиде SABC: треугольник АВС – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S. Сделать чертеж. Найти:

1. длину ребра АВ;

2. угол между ребрами АВ и AS;

3. угол наклона ребра AS к основанию пирамиды;

4. площадь основания пирамиды;

5. объем пирамиды;

6. уравнение прямой АВ;

7. уравнение плоскости АВС;

8. проекцию вершины S на плоскость АВС;

9. длину высоты пирамиды

SABC: А(-3;0;0); В(0;2;0); С(0;0;6); S(-3;4;5).

Решение

1) Длину ребра АВ находим по формуле расстояния между двумя точками:

2) Угол между рёбрами найдём по формуле косинуса угла между векторами , координаты которых определяются так:

3) Найдем координаты вектора

Найдем координаты вектора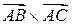

Он перпендикулярен плоскости (грани) ABC, поэтому угол между ребром AS и гранью ABC является дополнительным к углу α между векторами

α

φ

Отсюда получаем

4) Площадь определяем с помощью векторного произведения:

,

5) Объём пирамиды находится через вычисление смешанного произведения векторов Изучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. Формула для нахождения объема V пирамиды:

7) Запишем уравнение плоскости (ABC) перпендикулярной вектору , проходящей через точку А(-3;0;0)

6) Уравнение прямой , проходящей через точки

Канонические уравнения прямой, вектор направляющий вектор прямой

7) Запишем уравнение плоскости (ABC) перпендикулярной вектору , проходящей через точку А(-3;0;0)

8) Для определения проекции вершины на плоскость выполняютсяследующие действия:

а) составляется уравнение высоты пирамиды .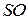

б) находится точка пересечения высоты и основания решением системы, содержащей уравнение высоты и уравнение плоскости.

Решение: SO –высота пирамиды, перпендикулярна плоскости (ABC), следовательно, прямая (SO) параллельна вектору или - нормали плоскости (ABC.

Он будет направляющим для По уравнению координаты вершины , т.е.

. Так как точка О – пересечение прямой (SO) и плоскости (ABC), то ее координаты удовлетворяют системе уравнений

, которую можно решить подстановкой

Подставив во второе уравнение, найдём значение , и следовательно значения

Точка 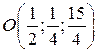- проекция точки на плоскость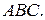

9) Длину высоты 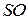пирамиды можно найти по формуле расстояния между точками S и O или по формуле расстояния d от точки до плоскости :

Изучите формулы самостоятельно, решив задание 9).