Условие, при котором три точки лежат на одной прямой

Три точки лежат на одной прямой в том и только том случае, если выполняется:

(28)

Эта формула показывает, что площадь треугольника ABC равна нулю.

2. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ.

Задача 1. Составить уравнение прямой проходящей через точку А(2;1) и через точку пересечения прямых.

Решение: 1)Найдём точку пересечения прямых:

(.)М

3) Используем формулу (11), составим уравнение прямой, проходящей через две точки:

;

, откуда и

Ответ:

Задача 2.Указать точку пересечения прямой и прямой

Решение: Реши систему:

;отсюда

Ответ: М (1;-2).

Задача 3. Найти уравнение прямой, проходящей через точку перечисления прямых и

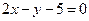и наклонной к оси ОХ под углом .

Решение: 1) Найдем точку пересечения прямых.

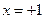
Прямая проходит через точку А (1;-3).

2)

3)Используя уравнение (9):

получим:

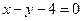
Ответ: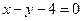

Задача 4. Найти уравнение прямой проходящей через точку D(-2;1) и середину отрезка AB, где A(2;7),B(4;3).

Решение: 1)Найти координаты середины отрезка AB.

т.е. точка M(3;5) – середина отрезка AB.

2) Искомая прямая проходит через точки:

M(3;5) и D(-2;1).Используем формулу (11)

по свойству пропорции:

-4(x-3)=-5(y-5)

-4x+12=-5y+25

-4x+5y+12-25=0

4x-5y+13=0

Ответ: 4x-5y+13=0

Задача 5. Найти уравнение прямой, проходящей через точку D(-3;4) параллельно прямой 2x-y+1=0.

Решение: 1)Найдём угловой коэффициент 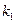прямой

2x-y+1=0

y=2x+1; 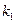=2

2) По условию параллельности прямых (формула 16)

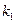= =2

3) т.к. искомая прямая проходит через точку D(-3;4) и имеет угловой коэффициент =2, от по формуле (9) имеем:

y-4=2(x+3)

y-4=2x+6

Откуда 2x-y+10=0

Ответ: 2x-y+10=0

Задача 6. Найти расстояние от точки A(-2:-2) до прямой

3x-2y+6=0

Решение: Используем формулу (2):

Ответ:

Задача 7. Найти уравнение прямой, проходящей через точку пересечения прямой с осью OX,

Перпендикулярно прямой

Решение: 1)Найдём угловой коэффициент 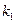прямой

y=-x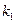+1; =-1; =1 (прямой )

2) Найдём координаты точки пересечения прямой ;

с осью OX,при этом y=0

3x+6=0; x=-2

(.)M(-2;0)

3) Искомая прямая проходит через (.)M(-2;0) и имеет

=1:

(y-0)=1(x+2)

y=x+2

x-y+2=0

Ответ: x-y+2=0

Задача 8. При каком значении параметра а прямые

перпендикулярны?

Решение: Представим уравнения прямых в виде: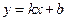

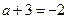
Ответ: .

Задача 9: Найти площадь треугольника с вершинами A(1;5),

Решение: Если считать A – первая вершина, B – вторая, C – третья, получим:

Ответ: усл. кв. ед.

Задача 10: Построить прямую

Решение: При при

Построим эти точки и проведём прямую через точки

3. ЗАДАЧНИК ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ.

Задача 1: Составить уравнение прямой, проходящей через точки .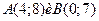

Ответ:

Задача 2: Дана прямая . Составить уравнение прямой, перпендикулярной данной и походящей через точку M(-3;1)

Ответ: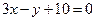

Задача 3: Найти координаты точки M, делящей отрезок BC в отношении 1:5, если даны точки B (1;0) и С (5;8).

Ответ:

Задача 4: Найти координаты точки С, делящей отрезок AB в отношении 3:1, если A (8;1); B (0;4).

Ответ: С (-4;5,5)

Задача 5: Даны три последовательные вершины параллелограмма.

Найти координаты четвёртой вершины параллелограмма.

Ответ: D (7;-10)

Задача 6. Найти центр тяжести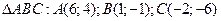

Ответ:

Задача 7: На прямой, проходящей через точку A (-5;5) и В (-1;2) найти точку, абсцисса которой x=3.

Ответ: М (3;-1)

Задача 8: Доказать, что треугольник с вершинами А (1;2), В (5;-2), С(10;3) прямоугольный.

Задача 9: Дан треугольник с вершинами: А (-1;4), В (5;3), С (2;-1). Определить длины сторон этого треугольника.

Ответ: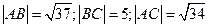

Задача 10: Определить траекторию точки М, которая при свеем движении всё время остаётся вдвое ближе к точке А (0;1), чем к точке В (0;4).

Ответ: Окружность с центром в начале координат.

Задача 11: Написать уравнение прямой, которая проходит через точку А (4;-3) и параллельна

а)оси абсцисс,

б) оси ординат,

в) прямой

Ответ: а) y=-3; б) x=4; в)2x-y-11=0

Задача 12: Написать уравнение прямой, которая проходит через точку А (-2;3) параллельно прямой

Ответ: .

Задача 13: Написать уравнениеперпендикуляра, опущенного из точки А (4;1) на прямую

Ответ:

Задача 14: Прямая проходит через середину отрезка АВ, где А (-2; 4), В (6;-8) и наклонна к оси ОХ под углом

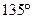. Найти ее уравнение.

Ответ:

Задача 15: При каком значении параметра прямые ; перпендикулярны друг другу?

Ответ:

Задача 16: Точки А (-4;1), В (5;2), С (1;3) являются вершинами треугольника. Написать уравнение высоты ВК.

Ответ:

Задача 17: Прямая является одной из сторон прямоугольника АВСD. Написать уравнения сторон этого прямоугольника через вершину А (-3;2).

Ответ: ;

Задача 18: Указать точку пересечения прямой и прямой

Ответ: М(-1;1)

Задача 19: В каком взаимном расположении находятся прямые:

19.1. 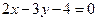и

Ответ: параллельны.

19.2. и

Ответ: пересекаются в точке А (2;3)

19.3. и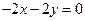

Ответ: совпадают

19.4. и

Ответ: перпендикулярны.

Задача 20.

Лежат ли на одной прямой три точки: А (-2;6); В (2;5); С (5;3).

Ответ: нет.