Пояснение 3 Доказательство Прокла

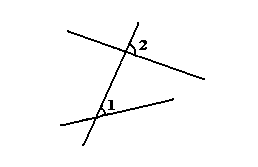
Ещё раз возвращаясь к двадцать седьмому предложению Начал приведу его здесь: < Если прямая падающая на две прямые, образует накрестлежащие углы, равные между собой, то прямые будут параллельны друг другу >

Это можно проиллюстрировать следующим рисунком –

–если угол 1 равен углу 2, то прямые параллельны, или, что тоже самое (пятнадцатое предложение Начал) если ∠1 = ∠3 то прямые параллельны. Евклид в Началах даёт этому предложению очень интересное доказательство восходящее (как я уже упомянуто) к предложению 16 и также к предложению 4. Однако я думаю эта теорема может быть обоснована исходя из девятой аксиомы Евклида следующим образом: пусть некоторую прямую, пересекают две другие (CE и DF) под равными (внешним и внутренним по одну сторону) углами. (как показано на рисунке)

Продолжим прямую AB неограниченно (обозначим эту неограниченную прямую (h)). Тогда мы имеем неограниченную прямую и восставленные на ней под одинаковыми углами (равными α) прямые BF и AE.

Если же, продолжаясь, они пересекутся, то значит, продолжаясь, пересекутся и прямые AC и BD восставленные на неограниченной прямой под одинаковыми, также равными α углами. (на том же расстоянии друг от друга) Если же и они, продолжаясь пересекаются, то прямые CE и DF продолжаясь каждая в обе стороны, пересекутся дважды и заключат пространство, что невозможно[51]. Значит, если некоторую прямую, пересекают две другие, под равными, (внешним и внутренним по одну сторону) углами, то эти прямые параллельны. Похожим образом эта теорема обосновывается в комментариях к первой книге Начал принадлежащих Д. Д. Мордухай – Болтовскому (эти комментарии входят в используемое издание Начал: НАЧАЛА ЕВКЛИДА КНИГИ I – VI Перевод с греческого и комментарии Д. Д. Мордухай – Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского Государственное издательство технико – теоретической литературы Москва · Ленинград · 1950.) Там обоснование данной теоремы сходное с этим помещено в комментарии пятьдесят восьмом и называется – «Приём Ома», и дана ссылка – Nhm, Ebene Raumwissenschaft, 2 Aufl., Berlin, 1835, §26, стр. 111.

Также, почти идентичное данному обоснование дано в книге Прокла Диадоха «Комментарии к первой книге «Начал»» в самом начале «раздела» Предложения: Часть 2. Прокл ссылается на некого Птолимея и начинает собственно само доказательство со слов: «А Птолимей в книге, где он пытается доказать, что прямые образующие углы…» Прокл Диадох Перевод А. И. Щетникова.

Литература

1. Евклид. Начала / Перевод с греческого и комментарии Д. Д. Мордухай – Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. Государственное издательство технико – теоретической литературы Москва · Ленинград · 1950.

2. Прокл Диадох. Комментарии к первой книге «Начал» / Перевод А. И. Щетникова.

3. Лобачевский Н. И. Геометрические исследования по теории параллельных линий // Н. И. Лобачевский «Избранные труды по геометрии» Редакция академика П. С. Александрова, Б. Н. Делоне и П. К. Рашевского. Издательство Академии Наук СССР Москва · 1956

4. Лобачевский Н. И. Новые начала Геометрии с полной теорией параллельных // Н. И. Лобачевский «Избранные труды по геометрии» Редакция академика П. С. Александрова, Б. Н. Делоне и П. К. Рашевского. Издательство Академии Наук СССР Москва · 1956

5. Лобачевский Н. И. Воображаемая Геометрия // Н. И. Лобачевский «Избранные труды по геометрии» Редакция академика П. С. Александрова, Б. Н. Делоне и П. К. Рашевского. Издательство Академии Наук СССР Москва · 1956

6. Перминов В. Я. Философия и основания математики. M., Прогресс-Традиция, 2001.

7. Перминов В. Я. Философское и методологическое мышление Н. И. Лобачевского // Историко-математические исследования. Вторая серия. Выпуск 12(47). М.: «Янус-К», 2007.

8. Перминов В. Я. Неевклидовы геометрии и философия математики И. Канта // История и методология естественных наук. Вып. XXV (Математика и механика). М., Изд-во Моск. ун-та, 1980.

9. Грязнов А. Ю. Методология физики и априоризм Канта // Вопросы философии. №8, 2000.

10. Грязнов А. Ю. Как философия влияет на физику // Классическая физика и теория познания. №1, 2015.

11. Кант И. Критика чистого разума / Пер. с нем. Н. Лосского сверен и отредактирован Ц. Г. Арзаканяном и М. И. Иткиным. Примеч. Ц. Г. Арзаканяна. – М.: Мысль, 1994.

12. Кант И. О форме и принципах чувственно воспринимаемого и интеллигибельного мира. 1770 // Кант И. Сочинения в 8-ми т. Т. 2. М.: Чоро, 1994.

13. Ефимов Н. В. Высшая геометрия. М., Физматлит, 2004.

14. Каган В. Ф. Лобачевский. Издательство Академии Наук ССР Москва-Ленинград 1948.

15. Каган В. Задача обоснования геометрии в современной постановке. Одесса. Типография Акционерного Южно-Русского Общества Печатного Дела. 1908.

16. Цингер В. Я. Недоразумения во взглядах на основания геометрии.

17. Цингер В. Я. Точные науки и позитивизм.

18. Щербаков Р. Н., Пичурин Л. Ф. Дифференциалы помогают геометрии: кн. для внеклас. чтения. IX–X кл. – М.: Просвещение, 1982.

19. Чернов С. А. Чистое созерцание и неевклидова геометрия // Кантовский сборник. Вып. 16. Калининград, 1991.

20. Энциклопедия элементарной математики. Книга четвёртая ГЕОМЕТРИЯ. Государственное издательство физикой математической литературы. М., 1963.

21. Челпанов. Г. И. Неогеометрия и её значение для теории познания. Об априорных элементах познания (понятие числа, времени, причинности, пространства.) Изд 2-е. – М.: ЛЕНАРД, 2016.

[1] геометрия Лобачевского и геометрия Римана

[2] Такой подход представлен в работе (речи) В. Кагана "Задача обоснования геометрии в современной постановке". Одесса. Типография Акционерного Южно–Русского Общества Печатного Дела. 1908.

А также, например, в книге Н. В. Ефимова "Высшая геометрия", М., Физматлит, 2004, гл. 1, §4.

[3] Такие линии существуют и на других поверхностях, кроме того прямыми могут называться не обязательно линии кратчайшего расстояния на кривых поверхностях. Под прямыми могут подразумеваться и, например, окружности, проведённые по определённым правилам на обычной плоскости. (см уже упомянутую мною работу Кагана, а также модели геометрии Лобачевского принадлежащие Клейну и Пуанкаре) (та модель Евклидовой геометрии о которой говорит Каган в упомянутой работе более подробно прокомментирована им в его работе – «Лобачевский», в главе ХХХ. «Интерпретации неевклидовой геометрии», а также довольно подробное разъяснение на эту тему содержится в книге: Энциклопедия элементарной математики. Книга четвёртая ГЕОМЕТРИЯ. Государственное издательство физикой математической литературы. М., 1963., в главе: АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИИЯ ГЕОМЕТРИИ (§4 Модели))

[4] Кроме того, надо отметить, что для нас совершенно не безразлично какую систему пространственных образом ассоциировать с геометрией в самом общем смысле этого слова. Понятно, что образы прямой и плоскости в их первоначальном смысле имеют куда большее значение и отношение к познанию пространства, чем, например, связки окружностей, которые (окружности) мы в общем то тоже можем называть прямыми.

[5] Быть может, я где то неточно отражу здесь взгляды этих великих учёных, но в общем то я буду говорить то, что соответствует их взглядам.

[6] Так можно представить себе все тела в природе частями одного целого, которое называем пространством. Н. И. Лобачевский «НОВЫЕ НАЧАЛА ГЕОМЕТРИИ С ПОЛНОЙ ТЕОРИЕЙ ПАРАЛЛЕЛЬНЫХ» Глава 1 ПЕРВЫЕ ПОНЯТИЯ В ГЕОМЕТРИИ.

[7] То есть Лобачевский не пытается заменить в науке понятие истины понятием соглашения или договорённости, – для него насколько можно судить из его трудов – истины это истины – просто аксиома о параллельных не очевидна. (точнее было бы сказать, что у Лобачевского есть свои определённые представления о геометрической науке, надо сказать, (по мнению автора этой статьи) – очень строгие и красивые – во многом похожие (по крайней мере по некоторой научной аккуратности – на представления Евклида)). Так вот из этих представлений Лобачевский и считает аксиому о параллельных не очевидной.

[8] Теорема Пифагора не выполняется в геометрии Лобачевского.

[9] Одиннадцатая аксиома первой книги Начал Евклида – дальше про неё ещё будет подробно сказано в пояснении 2. (В некотором смысле это та же самая аксиома о которой говорилось в предисловии)

[10] Предложение 29 первой книги Начал – оно формулируется так: < Прямая, падающая на параллельные прямые, образует накрестлежашие углы, равные между собой, и внешний угол, равный внутреннему, противолежащему с той же стороны, и внутренние односторонние углы, > вместе < равные двум прямым. >

[11] Это становится очевидным если вместо одиннадцатой аксиомы использовать доказанное нами (в пояснениях) из неё и обратно утверждение, что через точку не лежащую на прямой проходит только одна прямая параллельная данной.

[12] π это другое обозначение величины угла – два прямых 2∟.

[13] Так, благодаря тому, что сумма углов всех треугольников в Евклидовой геометрии одна и та же, мы, наперёд зная сумму углов всякого треугольника (она равна π) – по двум углам пересечения прямых с некоторой (двум углам треугольника)

можем определить и их угол пересечения между собой (третий угол треугольника)

[14] То, что линия (d), продолжаясь пересечёт линию (b) видно из девятой аксиомы – так, линия (d) не может уже пересечь второй раз линию (a). Линию (c) же она не может пересечь так как ей параллельна (линии (c) и (d) пересекают линию (a) под одинаковыми углами α2 = α). Значит, продолжаясь, линия (d) пересечёт линию (b).

[15] И равным ∑△ – ∟ – α = 2∟ – ∟ – α = ∟ – α

[16] Вообще же конечно Евклидовость может быть задана и через другие аксиомы и построения.

[17] Мы уже доказывали похожую теорему – что если треугольник разделён на два других и его сумма углов равна π то и сумма углов каждого из треугольников его составляющих равна π (и обратно)

[18] Это получается из–за аддитивности дефекта. Так, поскольку, в геометрии Лобачевского сумма углов всякого треугольника меньше двух прямых (у всякого треугольника есть дефект) и дефект треугольника составленного из двух других треугольников равен сумме дефектов

этих треугольников, то мы имеем треугольники с разным дефектом – и значит с разной суммой углов. Таковы, например, треугольник разделённый на два других и один из его составляющих или треугольник заключающий в себе другой треугольник и его заключаемый. (как на рисунке)

[19] β = ω, и значит в таком случае α + ω меньше двух прямых, а значит прямая (с) и прямая (а) пересекутся и пересекутся по ту же сторону от прямой (b), что и показано на рисунке.

[20] У Лобачевского термин «содержание сторон» обозначает – отношение сторон.

[21] Н.И. Лобачевский, вступление к его работе: НОВЫЕ НАЧАЛА ГЕОМЕТРИИ С ПОЛНОЙ ТЕОРИЕЙ ПАРАЛЛЕЛЬНЫХ.

[22] Метагеометрия (неогеометрия) – то же, что и неевклидова геометрия.

[23] Под изогенностью, которую Рёссель в своей книге называл сначала гомогенностью, он понимает то свойство пространства, в силу которого одна часть его ничем не отличается от другой, вследствие чего возможна свободная подвижность и относительность положения. Термин гомогенность он сохранил для другого свойства пространства. (сноска к понятию изогенности пространства, взята из статьи Челпанова)

[24] Существование абсолютной величины в геометрии Лобачевского можно объяснить на следующем примере. Пусть из некоторой точки (O) под углами 120 градусов друг к другу расходятся три «линии». Отложим теперь на них от центральной точки равные расстояния OA, OB и OC, и построим равносторонний треугольник ABC. (Очевидно, что и его углы тоже равны). Отложив теперь на этих «линиях» от точки (O) величину, превосходящую предыдущую, мы получим ещё один равносторонний треугольник – он будет заключать предыдущий, и что нетрудно доказать, он будет иметь сумму углов меньшую чем у предыдущего. Так каждой ещё большей откладываемой величине («радиусу») будет соответствовать ещё меньшая угловая величина. Значит в геометрии Лобачевского мы можем определить единицу длинны как радиус описанного геометрического построения при котором получается равносторонний треугольник с определённой суммой углов. Надо заметить, что в Евклидовом пространстве невозможно определить единицу измерения длинны связав её определение с самим пространством.

[25] Которая, как надо ещё раз обратить внимание, вызвана не тем, что мы видим евклидово пространство или, что его аксиомы нам более очевидны (что конечно тоже имеет место), а именно самим характером этих положений.

[26] Предложения 16 и 27 первой книги Начал.

[27] Здесь ничего не говорится о том, могут ли быть параллельными, прямые, которые пересекают некоторую под разными углами.

[28] 2∟ – символ, обозначающий угловую величину равную двум прямым углам (или π в радианной мере). Если некоторая прямая (f) восставлена на некоторой (e) то она всегда образует углы α и β вместе равные двум прямым углам (двум прямым). (тринадцатое предложение Начал)

[29] Имеется ввиду меньше двух прямых углов, взятых вместе, или в сумме

[30] Общая геометрия – так будем называть ту часть геометрии, доказательства которой не зависят от одиннадцатой аксиомы и которая служит основой для познания и геометрии Евклида и геометрии Лобачевского.

[31] Двадцать четвёртое предложение Начал, как и все первые 28 предложений, – имеют свои аналоги и в геометрии Лобачевского, так, что их можно использовать при доказательствах теорем общей геометрии.

[32] Здесь и далее имею ввиду – двум прямым углам, взятым вместе.

[33] Точнее на неограниченную линию (e) получающуюся из линии AB продолжением AB в обе стороны.

[34] То есть такой, что его меньшая сторона превысит любую, наперёд заданную величину.

[35] Кроме прямых (a) и KD

[36] Имеется ввиду предыдущий рисунок

[37] Это можно проиллюстрировать рисунком. Имеется ввиду угол1 = угол2, а ∠3 = ∠4.

[38] γ1 = ∟ /2 так как ∑△(D A1 K) = 2∟ = ∠FDK + α1 + γ1, а ∠FDK = ∟ → α1 + γ1 = ∟, но α1 = γ1 → γ1 = ∟ /2

[39] То есть дробь 1 /(2^n) может принимать значения меньшие любой наперёд заданной величины. Это видно из того, что её знаменатель может принимать значения большие любой наперёд заданной величины – то есть для любого N существует n, такое что 2^n > N. (Так будем считать очевидным, что увеличивая любую величину (в том числе и 2) каждый раз в два раза можно за конечное число шагов превысить любую наперёд заданную величину.)

[40] Имеется ввиду утверждение заменяющее в геометрии Лобачевского одиннадцатую аксиому и названное мной в самом начале этого пояснения «непохожим утверждением».

[41] Девятая аксиома первой книги Начал < И две прямые не содержат пространства >. Евклид имеет ввиду – две прямые не образуют замкнутого контура – не пересекаются дважды – не имеют двух общих точек.

[42] Девятая аксиома первой книги Начал < И две прямые не содержат пространства >. Евклид имеет ввиду – две прямые не образуют замкнутого контура – не пересекаются дважды – не имеют двух общих точек.

[43] Здесь и далее будем опираться на издание трудов Н. И. Лобачевского «ИЗБРАННЫЕ ТРУДЫ ПО ГЕОМЕТРИИ» Редакция академика П. С. Александрова, Б. Н. Делоне и П. К. Рашевского. ИЗДАТЕЛЬСТВО АКАДЕМИИ НАУК СССР МОСКВА · 1956

[44] Псевдосфера –

Рисунок взят из книги: Щербаков Р. Н., Пичурин Л. Ф. Дифференциалы помогают геометрии: кн. для внеклас. чтения. IX–X кл. – М.: Просвещение, 1982.

[45] Это «не похожее» утверждение, (как я его назвал в самом начале) выполняющее в геометрии Лобачевского роль одиннадцатой аксиомы, у Лобачевского – шестнадцатое предложение труда – «Геометрические исследования по теории параллельных линий» (входит в то же издание трудов Лобачевского).

[46] ∠5 + ∠4 + ∠3 это сумма углов треугольника MKD.

[47] так как ∠5 + ∠4 + угол1 = 2∟ (два прямых угла)

[48] Согласно пятнадцатому предложению Начал: < Если две прямые пересекаются, то образуют углы через вершину, равные между собой.>

[49] Ибо если бы угол пересечения «линий» был и углом между ними («линиями») как таковыми, то согласно приведённым рассуждениям мы бы имели то, что имеем в Евклидовой геометрии: в частности угол2 = угол1.

[50] Надо заметить – я бы не стал утверждать, что Н. И. Лобачевский считал их (да и своё пространство) совершенно непредставимыми – так в самом начале своего сочинения – ВООБРАЖАЕМАЯ ГЕОМЕТРИЯ (входит в то же издание трудов Лобачевского на которое я опираюсь) он пишет об этом так < Кто ни думал найти решение затруднительного вопроса, все без исключения ошибались, будучи предубеждены в справедливости того, что не может ещё следовать прямо из наших понятий о телах, без пособия наблюдений, как я, думаю, доказал это несомнительно в моём сочинении о началах Геометрии. > Под затруднительным вопросом Лобачевский подразумевает строгое математическое доказательство одиннадцатой аксиомы. В то же издание трудов входит его работа НОВЫЕ НАЧАЛА ГЕОМЕТРИИ С ПОЛНОЙ ТЕОРИЕЙ ПАРАЛЛЕЛЬНЫХ где Лобачевский приводит подробные размышления на эту тему.

[51] Девятая аксиома первой книги Начал < И две прямые не содержат пространства >. Евклид имеет ввиду – две прямые не образуют замкнутого контура – не пересекаются дважды – не имеют двух общих точек.