Контрольной работы № 1

Задача 1. Решить систему линейных алгебраических уравнений двумя способами: а) методом Крамера, б) матричным методом.

Решение:

а) Решим систему методом Крамера.

Составляем главный определитель системы, элементами которого являются коэффициенты при неизвестных:

и три вспомогательных определителя:

; ; .

Определитель составлен из определителя путем замены элементов первого столбца свободными членами системы уравнений. В определителях и соответственно второй и третий столбцы заменены свободными членами. Вычислим все четыре определителя по правилу треугольников:

.

Получаем:

Аналогично вычисляем:

;

;

.

Так как главный определитель системы , то система имеет единственное решение. Неизвестные , , 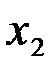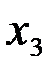находим по формулам Крамера:

; ; ;

Получаем, ; ; .

Ответ: (1; 1; 1)

б) Решим систему матричным методом.

Матрица коэффициентов перед неизвестными равна:

Столбец неизвестных: . Столбец свободных членов:

Найдем матрицу , обратную к матрице А. Обратная матрица существует, так как определитель матрицы А отличен от нуля:

.

Вычислим все алгебраические дополнения 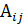, которые получаем путем вычеркивания i –ой строки и j- го столбца матрицы А. Причем, полученный таким образом определитель берем со знаком «+», если сумма номера строки и столбца число четное и со знаком «-», если эта сумма нечетная.

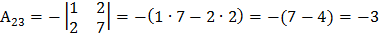
Составим обратную матрицу по формуле:

Получаем, .

Решение системы находим по формуле: .

Таким образом,

Х

Ответ: (1; 1; 1)

Задача 2. Даны координаты вершин треугольника АВС.

Найти: 1) уравнения сторон АВ и ВС и их угловые коэффициенты; 2) внутренний угол В; 3) уравнение и длину высоты СD; 4) площадь треугольника АВС.

А(2;1), В(-4;4), С(-1,5).

Решение:

1) Уравнения сторон АВ и АС найдем как уравнения прямых, проходящих через две заданные точки М₁ (x_1;y₁) и М₂(x₂;y₂) по формуле:

Для стороны АВ составляем уравнение прямой, проходящей через точки А(2;1) и В(-4;4). Получаем:

Умножим левую и правую часть на 3, получим:

Перемножая по правилу пропорции «крест- на- крест», получаем:

- уравнение стороны АВ.

Для тогочтобы найти угловой коэффициент этой прямой, приведем уравнение к виду , где k- угловой коэффициент прямой.

Выразим из полученного уравнения прямой АВ переменную “y”:

– угловой коэффициент прямой АВ.

Аналогично для стороны ВС:

- уравнение стороны ВС.

Преобразуем уравнение стороны ВС: .

Таким образом, - угловой коэффициент стороны ВС.

2) Внутренний угол В находим как угол между двумя прямыми АВ и ВС по формуле:

Получаем

Следовательно, угол В=45⁰.

3)Высота CD перпендикулярна стороне АВ. Известно, что если две прямые перпендикулярны, то их угловые коэффициенты связаны соотношением: . Тогда .

Составим уравнение высоты CD по формуле уравнения прямой, проходящей через данную точку с заданным угловым коэффициентом:

.

Прямая CD проходит через точку С(-1;5), =2. Получаем:

- уравнение высоты CD.

Длина высоты CD равна расстоянию от точки С до прямой АВ. Воспользуемся формулой вычисления расстояния от точки до прямой Ах+Ву+С=0:

Таким образом, подставляя координаты точки С(-1;5) и коэффициенты из уравнения прямой АВ (А=1 В=2 С= - 4), получаем:

длина высоты CD.

4) Площадь треугольника АВС равна: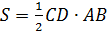

Длину стороны АВ находим как расстоянием между двумя точками А(2;1) и В(-4;4) по формуле:

Получаем: .

Тогда .

Ответ: 1) - уравнение стороны АВ; - уравнение стороны ВС; ; ; 2) В=45⁰; 3) - уравнение высоты CD; CD = 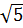; 4) S = .

Задача 3. Даны координаты вершин тетраэдра АВСD.

Найти: 1) координаты векторов АВ и АС; 2) угол между ребрами АВ и АС; 3) площадь грани АВС; 4) объем тетраэдра АВСD; 5) уравнение прямой АВ; 6) уравнения плоскостей АВС и ABD; 7) угол между плоскостями АВС и ABD.

A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).

Решение:

1)Если известны координаты точек А(x₁; y₁; z₁) B(x₂; y₂; z₂), то для нахождения координат вектора АВ необходимо от координат конца (точки В) вычесть соответствующие координаты начала (точки А) вектора. Получаем:

2)Угол между ребрами АВ и АС найдем как угол между двумя векторами по формуле:

Найдем длины векторов АВ и АС по формуле:

Получаем:

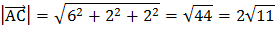
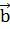
Скалярное произведение векторов и , заданных своими координатами, вычисляетсяпо формуле:

Тогда .

Таким образом, угол А между ребрами АВ и АС равен:

3) Площадь треугольника, построенного на векторах и равна:

,

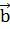
где векторное произведение векторов и , заданных своими координатами, находится по формуле:

.

Грань АВС представляет собой треугольник, построенный на векторах АВ и АС. Найдем векторное произведение этих векторов:

.

Найдем модуль векторного произведения:

Тогда искомая площадь равна:

4)Объем тетраэдра ABCD найдем используя геометрический смысл смешанного произведения векторов.

Объем тетраэдра, построенного на векторах находим по формуле: .

Смешанное произведение трех векторов, заданных своими координатами находится с помощью определителятретьего порядка:

.

Тетраэдр ABCD построен на векторах АВ, АС и AD. Найдем координаты вектора AD: (3; 7; 1). Тогда смешанное произведение равно:

Таким образом, объем пирамиды ABCDравен:

5)Уравнение прямой в пространстве проходящей через две точки и имеет вид: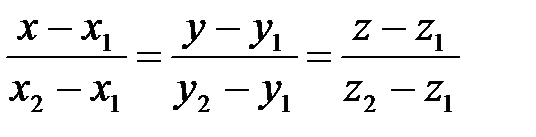

Составим уравнение прямой АВ, используя эту формулу:

уравнение прямой АВ.

6)Уравнение плоскости, проходящей через три точки , и , не лежащие на одной прямой имеет вид:

Используя эту формулу, составим уравнения плоскостей АВС и ABD.

Для плоскости АВС: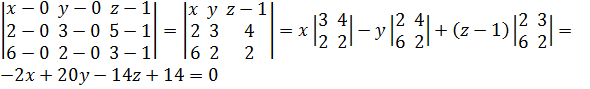

Разделим левую и правую часть на (-2). Следовательно, получим уравнение плоскости ABC: x-10y+7z-7=0.

Аналогично, для плоскости ABD:

Разделим левую и правую часть на (-5), получим: 5x – 2y- z +1 = 0- уравнение плоскости ABD.

7) Угол между плоскостями равен углу между их векторами нормали и вычисляется по формуле: .

Координаты вектора нормали плоскости равны коэффициентам при переменных x, y,zв общем уравнении плоскости.

Для плоскости АВС вектор нормали 1; -10; 7). Для плоскости ABD: .

Тогда косинус искомого угла равен:

Задача 4. Привести кривую второго порядка к каноническому виду и построить её.

а)

.

Решение: Данная линия является кривой второго порядка, в уравнении которой отсутствует произведение переменных и 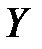. Дополним члены, содержащие , и члены, содержащие , до полных квадратов. Получим: , ,

Разделим левую и правую часть на 36, получим: .

Уравнение имеет вид

Это эллипс с центром в точке С(x₀; y₀). Таким образом, в нашей задаче мы имеем эллипс, центр которого лежит в точке , большая полуось , малая ось 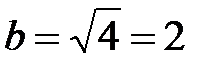(рис. 1).

y

3

-7 -4 -1 x

Рис. 1

б)

Решение: Уравнение кривой преобразуется следующим образом:

или .

Отсюда или .

Получили уравнение параболы вида с вершиной в точке , симметричной относительно оси .

Таким образом, мы имеем параболу (рис. 2), у которой вершина находится в точке , параметр , а ветви параболы направлены в отрицательную сторону оси .

y

1,5 x

Рис. 2

Для построения параболы найдем точки пересечения параболы с осью . Для этого положим и решим уравнение . Тогда , .

Имеем две точки и – точки пересечения параболы с осью .

в)

Решение: Для приведения уравнения кривой второго порядка к каноническому виду выделим полный квадрат относительно переменнойx:

Дополним до полного квадрата:

Свернув по формуле квадрата суммы, получаем:

Разделив на 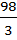, получим .

Уравнение имеет вид уравнения гиперболы

Таким образом, получаем гиперболу (рис. 3), центр которой находится в точке 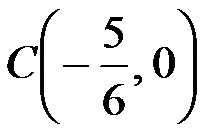, действительная полуось , мнимая полуось .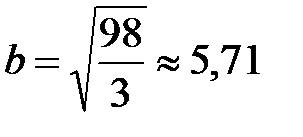

y

x

Рис. 3

Задача 5. Найти указанные пределы.

а) ; б) ; в) ;

г) ; д)

Решение:

а) Подставим в данную дробь вместо «х» значение к которому он стремится по условию, т. е. х = 6:

.

Получили неопределенность вида . Для того, чтобы избавиться от этой неопределенности необходимо разложить числитель и знаменатель дроби на множители.

Для этого воспользуемся формулой:

, где х₁, х₂- корни соответствующего квадратного уравнения.

Найдем корни квадратных трехчленов:

Аналогично:

Подставим найденные разложения в исходный предел. Получим:

б) Подстановка х = 5 приводит к неопределенности:

.

Умножим числитель и знаменатель на сопряженные им выражения и преобразуем полученные произведения по формуле:

Получаем:

в) В данном пределе получаем неопределенность вида . Для того, чтобы избавиться от этой неопределенности необходимо числитель и знаменатель дроби разделить на наивысшую степень х.

Разделим числитель и знаменатель на и учтем, что при .

Таким образом, получим:

г) Если данное выражение содержит тригонометрическую функцию и при подстановке значения х получаем неопределенность, то в этих случаях часто следует использовать первый замечательный предел и следствия из него:

.

Замечание: Следует помнить, что все эти формулы верны, когда функция делится на её аргумент. Например, .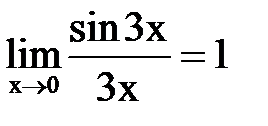

Вычислим данный в условии предел:

.

д) При вычислении предела показательно-степенной функции часто используют второй замечательный предел:

Широко используются также следствия из этой формулы:

.

Рассмотрим заданный предел .

Здесь , поэтому получим неопределенность вида .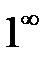

Так как , то преобразуем предел следующим образом:

= .

Обозначим тогда при , причем . Найдем предел основания: . Найдем предел показателя: .

Таким образом, данный предел = .

Задача 6. Найти производные данных функций.

а)

б) ; в) ; г)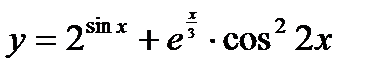

Решение:

а)

Перепишем данную функцию, записав слагаемые в виде степени: .

Находим производную сложной функции по формуле:

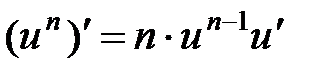
При вычислении производной используем также формулу:

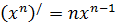
Тогда получаем:

.

б)

Преобразуем данную функцию, используя свойства логарифмов:

Найдем производную преобразованной функции, используя формулу :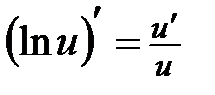

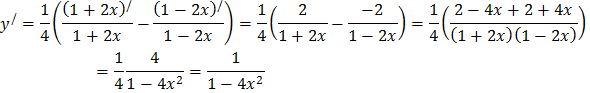
в) .

Найдем производную сложной функции, используя формулы:

;

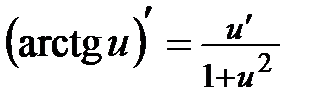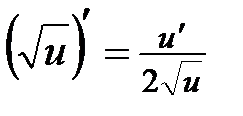
г)

При вычислении производной данной функции используем следующие правила и формулы дифференцирования:

;

; ;

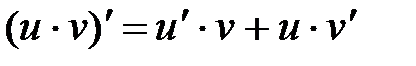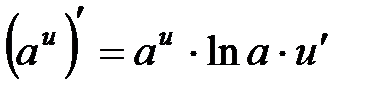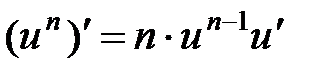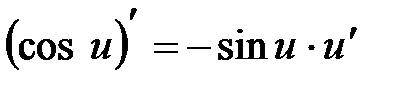
Получаем:

Задача 7. Исследовать средствами дифференциального исчисления функцию и построить ее график.

Решение:

1. Область определения данной функции представляет собой множество

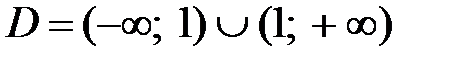
2. Пределы функции в точках разрыва и на концах области определения (данная функция имеет одну точку разрыва):

; ; .

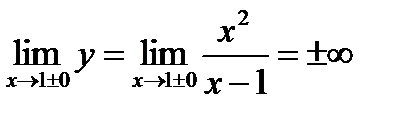3. Асимптоты. Если 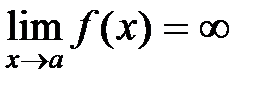, то прямая 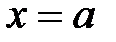— вертика льная асимптота.

В нашем случае вертикальная асимптота имеет уравнение .

Прямая является наклонной асимптотой, если существуют конечные пределы

и .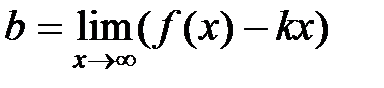

Найдем значения kи b:

,

Тогда наклонная асимптота имеет уравнение .

4. Точки пересечения графика с осями координат дают: во-первых,

нули функции (чтобы их найти, необходимо решить уравнение ) и, во-вторых, значение , если .

Так как для данной функции , то график проходит через точку О .

5. Симметрия. Функция – четная, если ;

ее график симметричен относительно оси .

Функция 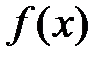– нечетная, если ; ее график симметричен относительно начала координат.

В нашем случае

; ,

т. е. и , следовательно функция общего вида, симметрии относительно осей координат у графика нет.

6. Периодичность. Если для некоторого числа выполняется равенство для всех , то функция – периодическая с периодом 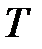. Очевидно, наша функция не является периодической.

7. Монотонность, экстремум функции.

Находим первую производную:

.

Находим критические точки (точки, в которых 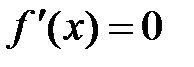или

не существует), отмечаем их на области определения функции, получаем интервалы знакопостоянства производной :

критические точки

Всюду в области определения первая производная существует.

Определяем знак производной в каждом интервале. Там, где 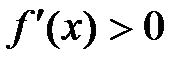, функция возрастает, а там, где ,она убывает. Если при переходе через критическую точку знак производной меняется с «+» на «-», то это точка максимума; если с «-» на «+», то точка минимума.

+ - - +

x

y 0 1 2

Получаем экстремальные значения:

.

8. Выпуклость, вогнутость, перегиб функции.

Вторая производная:

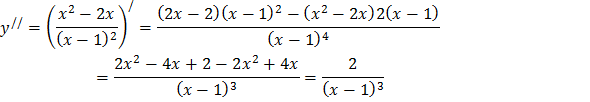
Находим точки, в которых или не существует, отмечаем их на области определения функции.

В данной задаче .Производная второго порядка не существует при x = 1.

Определяем знак производной в каждом интервале.

Кривая является вогнутой при тех значениях аргумента , при которых 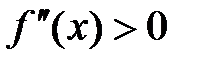). Кривая в точке является выпуклой, если в этой точке .

- +

∩ 1 x

Точек перегиба нет.

9. Строим график (если необходимо, находим несколько дополнительных точек) (рис. 4).

y

y=x

1 2 x

D MPE9sey+/OAwSjvU2g54knDX6TRJMu2wZbnQYE+rhqr95uAMvFXZeP7cutX+KeL6efF92+j3V2Ou r8bHB1CRxvgHw6++qEMpTjt/YBtUZyBdTFNBpUjuQAkwm2cy2Ak5n6Wgy0L/f6H8AQAA//8DAFBL AQItABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBl c10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxz Ly5yZWxzUEsBAi0AFAAGAAgAAAAhAKvAwO/xAwAAhAoAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9l Mm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAB/V0a/fAAAACgEAAA8AAAAAAAAAAAAAAAAASwYAAGRy cy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAABXBwAAAAA= " path="m,840549c267493,568293,534987,296037,695325,164274,855663,32511,889000,-62738,962025,49974v73025,112712,171450,790575,171450,790575l1133475,840549e" filled="f" strokecolor="black [3040]"> -1

Рис. 4

Задача 8. Дана функция , точка 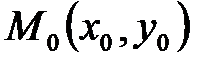, вектор 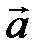. Требуется: а) исследовать функцию на экстремум;

б) Составить уравнения касательной плоскости и нормали в точке ;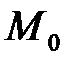

в) найти производную функции 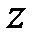в направлении вектора 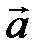в точке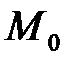

; M₀ (1; - 2),