 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Спряження дуг між собою
|
|
Зовнішнє спряження
 Послідовність виконання:
Послідовність виконання:
1. З центра О1 проводять допоміжну дугу радіусом R + R1.
2. З центра О2 проводять допоміжну дугу радіусом R + R2.
3. У точці перетину допоміжних дуг міститься центр спряження О.
4. З’єднують центр спряження О з центром спряжуваного кола О1.
На перетині прямої ОО1 з дугою кола одержують точку А.
5. З’єднують центр спряження О з центром спряжуваного кола О2. На перетині прямої ОО2 з дугою кола одержують точку В.
6. Поставивши опорну ніжку циркуля в точку О, розхилом циркуля, що дорівнює радіусу спряження R, між точками А і В проводять дугу, яка утворює плавний перехід від дуги одного кола до дуги іншого кола.
Внутрішнє спряження
Послідовність виконання:
1. 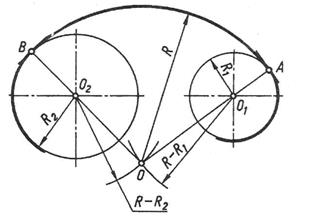 З центра О1 проводять допоміжну дугу радіусом R – R1.
З центра О1 проводять допоміжну дугу радіусом R – R1.
2. З центра О2 проводять допоміжну дугу радіусом R – R2.
3. У точці перетину допоміжних дуг міститься центр спряження О.
4. З’єднують центр спряження О з центром спряжуваного кола О1. На перетині прямої ОО1 з дугою кола одержують точку А.
5. З’єднують центр спряження О з центром спряжуваного кола О2. На перетині прямої ОО2 з дугою кола одержують точку В.
6. Поставивши опорну ніжку циркуля в точку О, розхилом циркуля, що дорівнює радіусу спряження R, між точками А і В проводять дугу, яка утворює плавний перехід від дуги одного кола до дуги іншого кола.
Змішане спряження
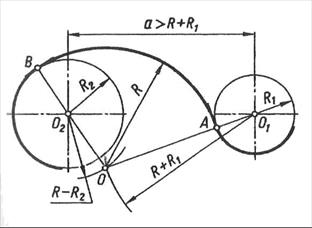
Послідовність виконання:
1. З центра О1 проводять допоміжну дугу радіусом R + R1.
2. З центра О2 проводять допоміжну дугу радіусом R – R2.
3. У точці перетину допоміжних дуг міститься центр спряження О.
4. З’єднують центр спряження О з центром спряжуваного кола О1. На перетині прямої ОО1 з дугою кола одержують точку А.
5. З’єднують центр спряження О з центром спряжуваного кола О2. На перетині прямої ОО2 з дугою кола одержують точку В.
6. Поставивши опорну ніжку циркуля в точку О, розхилом циркуля, що дорівнює радіусу спряження R, між точками А і В проводять дугу, яка утворює плавний перехід від дуги одного кола до дуги іншого кола.
3.3. УКЛОН І КОНУСНІСТЬ
Уклон. Багато деталей мають похилі поверхні. Їх нахил відносно інших поверхонь на кресленнях задають за допомогою величини уклону. Уклони мають поверхні профілів прокату: рейки, швелери, таврові балки.

Рис. 3.17. Елементи технічних поверхонь з уклонами
Уклоном називають величину, що характеризує нахил прямої лінії відносно іншої прямої (горизонтальної або вертикальної).
Характеризують уклон відношенням довжин катетів прямокутного трикутника АВС:
і = 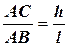

Рис. 3.18. Побудова уклону
Наведене співвідношення вказує на те, що побудова відрізка СВ зі заданим уклоном до відрізка АВ може бути зведена до побудови гіпотенузи прямокутного трикутника АВС, у якого відношення довжин катетів АС і АВ відповідає цьому уклону.
Отже, якщо потрібно провести лінію з уклоном, наприклад, 1:5 відносно заданої, то до заданої прямої проводять перпендикуляр і на ньому відкладають один відрізок довільної величини, а на заданій прямій – п’ять таких відрізків. З’єднавши між собою кінцеві точки обох відрізків, одержують заданий уклон (рис. 3.19).

Рис. 3.19. Побудова уклону
Вказують на кресленнях уклони у вигляді числових співвідношень (1:3; 1:5; 1:8; 1:10 і т.д.) або в відсотках (10%; 12%). Перед числовим співвідношенням наносять знак  . Його гострий кут спрямовують в бік нахилу. Вказують величину уклону на поличці лінії-виноски, проведеної від лінії з нахилом. Починають лінію-виноску стрілкою. Поличку лінії-виноски та вказані на ній знак і розмірне число розміщують паралельно до напрямку, відносно якого задано уклон на кресленні.
. Його гострий кут спрямовують в бік нахилу. Вказують величину уклону на поличці лінії-виноски, проведеної від лінії з нахилом. Починають лінію-виноску стрілкою. Поличку лінії-виноски та вказані на ній знак і розмірне число розміщують паралельно до напрямку, відносно якого задано уклон на кресленні.

Рис.3.20. Позначення уклону
Конусність. На кресленні деталі для точно обробленої конічної поверхні вказують конусність. Таку поверхню мають центри задньої бабки токарного верстата, хвостовики металорізальних інструментів, перехідних втулок для них тощо.

Рис. 3.21. Поверхні деталей з конусністю
К о н у с н і с т ю називають відношення різниці діаметрів основ конуса до відстані між ними:
К = 

Рис. 3.22. Побудова конусності
Якщо конічна поверхня є повним конусом, то конусність визначають як відношення діаметра основи конуса до його висоти:
К = 
На кресленнях конусність, як і уклон, вказують у числових співвідношеннях.
При позначенні величини конусності на кресленні перед числовим співвідношенням наносять знак  у вигляді рівнобедреного трикутника. Його вершину спрямовують в бік вершини конуса. Вказують величину конусності над віссю усередині контуру зображення конічної поверхні або на поличці лінії-виноски, проведеної від лінії контуру зображення, що відповідає твірній конуса. Позначення величини конусності, поличку лінії-виноски, вказані на ній знак і розмірне число розміщають паралельно до геометричної осі контуру зображення конічної поверхні.
у вигляді рівнобедреного трикутника. Його вершину спрямовують в бік вершини конуса. Вказують величину конусності над віссю усередині контуру зображення конічної поверхні або на поличці лінії-виноски, проведеної від лінії контуру зображення, що відповідає твірній конуса. Позначення величини конусності, поличку лінії-виноски, вказані на ній знак і розмірне число розміщають паралельно до геометричної осі контуру зображення конічної поверхні.

Рис. 3.23. Позначення конусності
Щоб накреслити контур зображення конічної поверхні, достатньо знати величину її конусності, діаметр однієї з основ конуса і довжину конічної поверхні. Діаметр другої основи конуса розраховують.
D = d + Kl; d = D - Kl.
При заданій конусності, діаметрах обох основ визначають довжину конічної поверхні:

3.4. ЛЕКАЛЬНІ КРИВІ
Л е к а л ь н и м и називають криві лінії, які креслять за допомогою лекал за попередньо побудованими точками.
Лекало – це плоска фігурна лінійка, яка має різну кривизну кромок на ділянках, що плавно переходять одна в одну. Обведення ділянок кривої за допомогою лекала здійснюють послідовно, пересуваючи або міняючи лекало. Кривизну ділянки лекала кожного разу добирають так, щоб за його допомогою було можливо з’єднувати не менше чотирьох точок.

Рис.3.24. Проведення кривої лінії за допомогою лекала
До лекальних кривих належать еліпс, парабола, гіпербола, спіраль Архімеда, евольвента кола, синусоїда та деякі інші.
Еліпс – це плоска замкнена крива. Форму еліпса мають поширені у різних механізмах ексцентрики та кулачки. Дугою еліпса обмежуються похилі зрізи на циліндричних поверхнях.

Рис. 3.25. Еліпси
Розмірами, що визначають величину еліпса, є розміри його осей – великої АВ і малої СD. За ними виконують побудову еліпса.
Починають побудову з проведення двох концентричних кіл, що мають спільний центр О: діаметр більшого кола дорівнює величині великої осі еліпса АВ, а меншого – величині малої осі СD (рис. 3.26 а).
Далі ділять більше коло на рівну кількість частин (наприклад, на 12 частин). Точки поділу з’єднують з центром О. Ці прямі поділять менше коло також на 12 рівних частин (рис. 3.26 б).
З точок поділу на більшому колі (за винятком точок 1, 4, 7 і 10) проводіть вертикальні відрізки (рис. 3.26 в). З точок поділу на меншому колі (за винятком точок с і d) проводять горизонтальні відрізки до перетину з відповідними їм за номерами вже проведеними вертикальними відрізками (рис. 3.26 г).
Утворені точки перетину, включаючи і точки a, b, c, d, належать еліпсу. За допомогою лекала їх з’єднують плавною кривою, яка і є еліпсом (рис. 3.26 д).
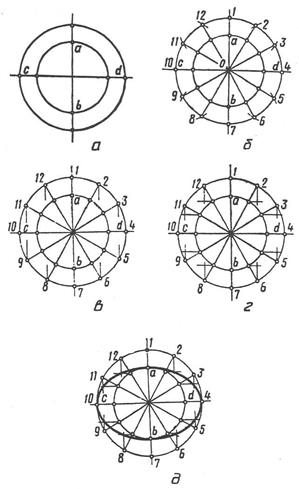
Рис. 3.26. Послідовність побудови еліпса
Спіраль Архімеда – це плоска крива, яку описує точка площини, що рівномірно обертається навколо центра О і рівномірно віддаляється від нього. Форму спіралі Архімеда мають спіральна пружина і робоча поверхня диска самоцентруючого токарного патрона.

Рис. 3.27. Спіраль Архімеда
Побудову спіралі Архімеда виконують за розміром її кроку S, що є відстанню, на яку віддаляється точка від центра у процесі свого обертання за один оберт. Здійснивши повний оберт, точка описує виток спіралі (рис. 3.28 а). За другий повний оберт вона утворює ще один виток (рис. 3.28 б).

Рис. 3.28. Утворення спіралі Архімеда
а – один виток спіралі; б – два витка спіралі
Починають побудову з проведення кола радіусом, що дорівнює кроку спіралі S. Проведене коло ділять на рівну кількість частин (наприклад, на 8 частин). Точки поділу з’єднують з центром кола. Один з радіусів кола ділять на рівні частини, число яких повинно дорівнювати числу поділок на колі (в прикладі радіус поділено на 8 рівних частин).
З центра О радіусами О1 , О2 і т.д. проводять дуги до перетину з радіусами відповідних номерів. Тобто з точки поділу 1 на радіусі проводять дугу до радіуса, проведеного в точку 1 на колі, з точки 2 – до радіуса, проведеного в точку 2 кола і т.д. Послідовно проведені дуги утворюють на радіусах точки I, II, III, IV, V, VI, VII i VIII – вони належать спіралі. Ці точки плавно з’єднують між собою за допомогою лекала. Утворена таким чином крива і буде спіраллю Архімеда.

Рис.3.29. Побудова спіралі Архімеда
Евольвента кола – це плоска крива, яку описує точка прямої лінії, що котиться без ковзання по колу. Дуга евольвенти окреслює контури зубів зубчастих коліс.


Рис. 3.30. Евольвента кола
Побудову евольвенти кола виконують за розміром діаметра її твірного кола D.
Починають побудову евольвенти з поділу кола заданого діаметра D на рівне число частин (наприклад, на 12 частин) (рис. 3.31). Точки поділу на колі нумерують. Ці точки з’єднують з центром кола. Через кожну точку поділу до кола проводять дотичну (найзручніше це зробити за допомогою прямокутного косинця і лінійки, пам’ятаючи про те, що дотична до кола перпендикулярна до радіуса кола, проведеного в точку дотику).
На дотичній, проведеній до 12-ї поділки, відкладають довжину кола, що дорівнює  . Цю довжину так само ділять на 12 рівних частин, кожна з яких дорівнює 1/12 довжини кола.
. Цю довжину так само ділять на 12 рівних частин, кожна з яких дорівнює 1/12 довжини кола.
На першій дотичній до кола від точки 1 відкладають відрізок, що дорівнює 1/12 довжини кола, і одержують точку І; на другій дотичній відкладають відповідно 2/12 і одержують точку ІІ; на третій – 3/12 і одержують точку ІІІ, на четвертій – 4/12 і одержують точку IV і т.д.
Утворені на дотичних до кола точки І, ІІ, ІІІ, … ХІІ належать евольвенті. Тому, з’єднавши їх плавно за допомогою лекала, одержують евольвенту кола.

Рис. 3.31. Побудова евольвенти кола
Парабола – це плоска незамкнена крива, по якій виконують контури плавних переходів у тих місцях основних деталей машин, де виникає потреба забезпечити максимальну міцність і жорсткість конструкції без збільшення ваги самої деталі.

Рис. 3.32
Існують різні способи побудови параболи на контурах зображень технічних креслень:
І. За заданою вершиною і будь-якою точкою.
Побудову параболи починають з побудови допоміжного прямокутника ОАВС (рис. 3.33). Довжини його сторін ОА = l1 і ОС = l2 визначають положення заданої точки В. Його сторони ОА і ОВ ділять на однакове число рівних частин. Точки поділу нумерують. Верхній ряд точок з’єднують з вершиною О, а через ряд лівих точок проводять прямі лінії, паралельні до осі параболи. Взаємний перетин горизонтальних прямих 1, 2, 3, … з променями 0-1, 0-2, 0-3 і т.д. утворює точки I, II, III,IV, V, VI i VII, що належать параболі.

Рис. 3.33
ІІ. Вписування параболи в заданий кут.
Для побудови параболи сторони заданого кута ОАВ ділять на однакову кількість рівних частин (рис. 3.34). Точки поділу на одній стороні кута нумерують у порядку зростання (1, 2, 3, …6), на іншій – за зменшенням (6, 5, 4, … 1) від вершини кута О. Далі точки поділу з однаковими номерами з’єднують відрізками прямої. Дотична крива, проведена до них за допомогою лекала, і буде параболою.
Кут, в який вписують параболу, може бути гострим чи тупим.

Рис. 3.34
Дата публикования: 2015-09-18; Прочитано: 3789 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
