Ожерелья

Задача "ожерелья" — это одна из классических комбинаторных задач. Требуется посчитать количество различных ожерелий из 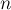бусинок, каждая из которых может быть покрашена в один из цветов. При сравнении двух ожерелий их можно поворачивать, но не переворачивать (т.е. разрешается сделать циклический сдвиг).

Решение

Решить эту задачу можно, используя лемму Бернсайда и теорему Пойа. [ Ниже идёт копия текста из этой статьи ]

В этой задаче мы можем сразу найти группу инвариантных перестановок. Очевидно, она будет состоять из 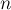перестановок:

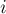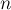Найдём явную формулу для вычисления . Во-первых, заметим, что перестановки имеют такой вид, что в -ой перестановке на -ой позиции стоит (взятое по модулю , если оно больше 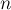). Если мы будем рассматривать циклическую структуру 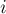-ой перестановки, то увидим, что единица переходит в , переходит в , — в , и т.д., пока не придём в число ; для остальных элементов выполняются похожие утверждения. Отсюда можно понять, что все циклы имеют одинаковую длину, равную , т.е. 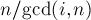("gcd" — наибольший общий делитель, "lcm" — наименьшее общее кратное). Тогда количество циклов в 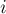-ой перестановке будет равно просто .

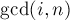Подставляя найденные значения в теорему Пойа, получаем решение:

Можно оставить формулу в таком виде, а можно её свернуть ещё больше. Перейдём от суммы по всем 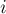к сумме только по делителям 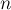. Действительно, в нашей сумме будет много одинаковых слагаемых: если 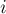не является делителем 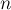, то таковой делитель найдётся после вычисления 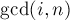. Следовательно, для каждого делителя его слагаемое учтётся несколько раз, т.е. сумму можно представить в таком виде:

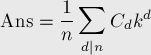
где — это количество таких чисел 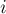, что . Найдём явное выражение для этого количества. Любое такое число 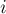имеет вид: , где (иначе было бы ). Вспоминая функцию Эйлера, мы находим, что количество таких — это величина функции Эйлера . Таким образом, , и окончательно получаем формулу:

Задача о ферзях

int SIZE = 0;

int board[13][13];

int results_count = 0;

void showBoard()

{

for(int a = 0; a < SIZE; ++a)

{

for(int b = 0; b < SIZE; ++b)

{

std::cout << ((board[a][b])? "Q ": ". ");

}

std::cout << '\n';

}

}

bool tryQueen(int a, int b)

{

for(int i = 0; i < a; ++i)

{

if(board[i][b])

{

return false;

}

}

for(int i = 1; i <= a && b-i >= 0; ++i)

{

if(board[a-i][b-i])

{

return false;

}

}

for(int i = 1; i <= a && b+i < SIZE; i++)

{

if(board[a-i][b+i])

{

return false;

}

}

return true;

}

void setQueen(int a) {

if(a == SIZE)

{

results_count++;

return;

}

for(int i = 0; i < SIZE; ++i)

{ if(tryQueen(a, i))

{

board[a][i] = 1;

setQueen(a+1);

board[a][i] = 0;

}

}

return;

}

int main()

{

std::cin >> SIZE;

setQueen(0);

std::cout << results_count << std::endl;

return 0;

}

36)Ханойские башни

void hanoi_towers(int quantity, int from, int to, int buf_peg) {

if (quantity!= 0)
{
hanoi_towers(quantity-1, from, buf_peg, to);

cout << from << ' ' << to << endl;

hanoi_towers(quantity-1, buf_peg, to, from);
}
}

int main()
{
setlocale(LC_ALL,"rus");
int start_peg=1, destination_peg=2, buffer_peg=3, plate_quantity;
cin >> plate_quantity;

hanoi_towers(plate_quantity, start_peg, destination_peg, buffer_peg);
return 0;
}