Числа Каталана

Числа Каталана — числовая последовательность, встречающаяся в удивительном числе комбинаторных задач.

Первые несколько чисел Каталана (начиная с нулевого):

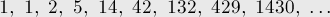
Числа Каталана встречаются в большом количестве задач комбинаторики. 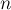-ое число Каталана — это:

Количество корректных скобочных последовательностей, состоящих из 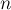открывающих и 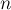закрывающих скобок.

Количество корневых бинарных деревьев с листьями (вершины не пронумерованы).

Количество способов полностью разделить скобками множитель.

Количество триангуляций выпуклого -угольника (т.е. количество разбиений многоугольника непересекающимися диагоналями на треугольники).

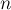Количество способов соединить точек на окружности непересекающимися хордами.

Количество неизоморфных полных бинарных деревьев с 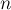внутренними вершинами (т.е. имеющими хотя бы одного сына).

Количество монотонных путей из точки в точку 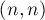в квадратной решётке размером , не поднимающихся над главной диагональю.

Количество перестановок длины 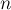, которые можно отсортировать стеком (можно показать, что перестановка является сортируемой стеком тогда и только тогда, когда нет таких индексов , что ).

Количество непрерывных разбиений множества из 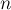элементов (т.е. разбиений на непрерывные блоки).

Количество способов покрыть лесенку с помощью 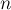прямоугольников (имеется в виду фигура, состоящая из 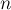столбцов, 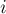-ый из которых имеет высоту ).

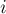Вычисление

Имеется две формулы для чисел Каталана: рекуррентная и аналитическая. Поскольку мы считаем, что все приведённые выше задачи эквивалентны, то для доказательства формул мы будем выбирать ту задачу, с помощью которой это сделать проще всего.

Рекуррентная формула

Рекуррентную формулу легко вывести из задачи о правильных скобочных последовательностях.

Самой левой открывающей скобке l соответствует определённая закрывающая скобка r, которая разбивает формулу две части, каждая из которых в свою очередь является правильной скобочной последовательностью. Поэтому, если мы обозначим , то для любого фиксированного будет ровно способов. Суммируя это по всем допустимым , мы и получаем рекуррентную зависимость на .

Аналитическая формула

(здесь через обозначен, как обычно, биномиальный коэффициент).

Эту формулу проще всего вывести из задачи о монотонных путях. Общее количество монотонных путей в решётке размером равно . Теперь посчитаем количество монотонных путей, пересекающих диагональ. Рассмотрим какой-либо из таких путей, и найдём первое ребро, которое стоит выше диагонали. Отразим относительно диагонали весь путь, идущий после этого ребра. В результате получим монотонный путь в решётке . Но, с другой стороны, любой монотонный путь в решётке обязательно пересекает диагональ, следовательно, он получен как раз таким способом из какого-либо (причём единственного) монотонного пути, пересекающего диагональ, в решётке . Монотонных путей в решётке имеется 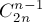. В результате получаем формулу: