Алгоритм Куна нахождения наибольшего паросочетания в двудольном графе

Дан двудольный граф 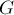, содержащий 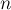вершин и 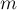рёбер. Требуется найти наибольшее паросочетание, т.е. выбрать как можно больше рёбер, чтобы ни одно выбранное ребро не имело общей вершины ни с каким другим выбранным ребром.

Теорема Бержа

Формулировка. Паросочетание является максимальным тогда и только тогда, когда не существует увеличивающих относительно него цепей.

int n, k;

vector < vector<int> > g;

vector<int> mt;

vector<char> used;

bool try_kuhn (int v) {

if (used[v]) return false;

used[v] = true;

for (size_t i=0; i<g[v].size(); ++i) {

int to = g[v][i];

if (mt[to] == -1 || try_kuhn (mt[to])) {

mt[to] = v;

return true;

}

}

return false;

}

int main() {

... чтение графа...

mt.assign (k, -1);

vector<char> used1 (n);

for (int i=0; i<n; ++i)

for (size_t j=0; j<g[i].size(); ++j)

if (mt[g[i][j]] == -1) {

mt[g[i][j]] = i;

used1[i] = true;

break;

}

for (int i=0; i<n; ++i) {

if (used1[i]) continue;

used.assign (n, false);

try_kuhn (i);

}

for (int i=0; i<k; ++i)

if (mt[i]!= -1)

printf ("%d %d\n", mt[i]+1, i+1);

}

12)Эйлер

int phi (int n) {

int result = n;

for (int i=2; i*i<=n; ++i)

if (n % i == 0) {

while (n % i == 0)

n /= i;

result -= result / i;

}

if (n > 1)

result -= result / n;

return result;

}

Binpow

int binpow (int a, int n) {

int res = 1;

while (n) {

if (n & 1)

res *= a;

a *= a;

n >>= 1;

}

return res;

}