Поиск точек сочленения

Пусть дан связный неориентированный граф. Точкой сочленения (или точкой артикуляции, англ. "cut vertex" или "articulation point") называется такая вершина, удаление которой делает граф несвязным.

vector<int> g[MAXN];

bool used[MAXN];

int timer, tin[MAXN], fup[MAXN];

void dfs (int v, int p = -1) {

used[v] = true;

tin[v] = fup[v] = timer++;

int children = 0;

for (size_t i=0; i<g[v].size(); ++i) {

int to = g[v][i];

if (to == p) continue;

if (used[to])

fup[v] = min (fup[v], tin[to]);

else {

dfs (to, v);

fup[v] = min (fup[v], fup[to]);

if (fup[to] >= tin[v] && p!= -1)

IS_CUTPOINT(v);

++children;

}

}

if (p == -1 && children > 1)

IS_CUTPOINT(v);

}

int main() {

int n;

... чтение n и g...

timer = 0;

for (int i=0; i<n; ++i)

used[i] = false;

dfs (0);

}

Здесь константе 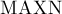должно быть задано значение, равное максимально возможному числу вершин во входном графе.

Функция 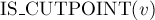в коде — это некая функция, которая будет реагировать на то, что вершина 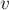является точкой сочленения, например, выводить эту вершины на экран (надо учитывать, что для одной и той же вершины эта функция может быть вызвана несколько раз).

8)Дейкстра

const int INF = 1000000000;

int main() {

int n;

... чтение n...

vector < vector < pair<int,int> > > g (n);

... чтение графа...

int s =...; // стартовая вершина

vector<int> d (n, INF), p (n);

d[s] = 0;

vector<char> u (n);

for (int i=0; i<n; ++i) {

int v = -1;

for (int j=0; j<n; ++j)

if (!u[j] && (v == -1 || d[j] < d[v]))

v = j;

if (d[v] == INF)

break;

u[v] = true;

for (size_t j=0; j<g[v].size(); ++j) {

int to = g[v][j].first,

len = g[v][j].second;

if (d[v] + len < d[to]) {

d[to] = d[v] + len;

p[to] = v;

}

}

}

}

9) Эратосфен

int n;

vector<char> prime (n+1, true);

prime[0] = prime[1] = false;

for (int i=2; i<=n; ++i)

if (prime[i])

if (i * 1ll * i <= n)

for (int j=i*i; j<=n; j+=i)

prime[j] = false;

Задача о назначениях

Задача имеет две эквивалентные постановки:

Дана квадратная матрица A[1..N,1..N]. Нужно выбрать в ней N элементов так, чтобы в каждой строке и столбце был выбран ровно один элемент, а сумма значений этих элементов была наименьшей.

Имеется N заказов и N станков. Про каждый заказ известна стоимость его изготовления на каждом станке. На каждом станке можно выполнять только один заказ. Требуется распределить все заказы по станкам так, чтобы минимизировать суммарную стоимость.

vector<int> u (n+1), v (m+1), p (m+1), way (m+1);

for (int i=1; i<=n; ++i) {

p[0] = i;

int j0 = 0;

vector<int> minv (m+1, INF);

vector<char> used (m+1, false);

do {

used[j0] = true;

int i0 = p[j0], delta = INF, j1;

for (int j=1; j<=m; ++j)

if (!used[j]) {

int cur = a[i0][j]-u[i0]-v[j];

if (cur < minv[j])

minv[j] = cur, way[j] = j0;

if (minv[j] < delta)

delta = minv[j], j1 = j;

}

for (int j=0; j<=m; ++j)

if (used[j])

u[p[j]] += delta, v[j] -= delta;

else

minv[j] -= delta;

j0 = j1;

} while (p[j0]!= 0);

do {

int j1 = way[j0];

p[j0] = p[j1];

j0 = j1;

} while (j0);

}