Аксиоматическое определение вероятности

Сформулируем аксиомы теории вероятностей.

Пусть Ω – пространство элементарных событий некоторого стохастического эксперимента и в Ω выделена система F событий, являющаяся алгеброй событий. Это означает, что

Ω F;

если А F ;

если А и В F .

Предположим, что каждому событию А F поставлено в соответствие число р(А) – вероятность случайного события А и верны свойства:

1) р(А) для любого А F;

2) р(Ω)=1;

3) если А и В несовместны, то р(А+В)=р(А)+р(В)

Утверждение. Два события являются независимыми, если исход одного события не влияет на исход другого события.

Пример. Эксперимент состоит в том, что 2 стрелка стреляют по мишени. События А₁={1 стрелок попал}, А₂={2 стрелок попал} являются независимыми, так как стрелки стреляют независимо друг от друга - результат попадания 1-го стрелка никак не влияет на попадание или промах 2-го стрелка.

Ниже мы докажем теорему. Если А и В – независимые события, то вероятность произведения этих событий равна произведению вероятностей событий, Р(А·В)=Р(А)·Р(В).

Пример. В урне лежит 5 черных шаров, 4 красных и 3 белых. Последовательно вынимают 3 шара, причем каждый шар возвращают в урну прежде, чем вынимают следующий. Найти вероятность того, что 1-ый вынутый шар – черный, 2-ой – красный,

3-ий – белый.

Решение. Отразим условие задачи на схеме:

12 шаров

5 черных 4 красных 3 белых

Введем событие, вероятность которого надо найти: А={1-ый вынутый шар – черный, 2-ой – красный, 3-ий – белый}.

Выделим события: А₁={1-ый вынутый шар - черный};

А₂={2-ой вынутый шар - красный};

А₃={3-ий вынутый шар - белый}.

Вычислим вероятности событий А₁, А₂, А₃: Р(А₁)= . Поскольку первый шар возвращается в урну, то прежде, чем вынуть второй шар, в урне находится 12 шаров из них 4 красных. Значит, Р(А₂)= .

Аналогично рассуждая, получим, что Р(А₃)= .

Выразим событие А через события A₁, A₂ и A₃ : А= А₁·А₂·А₃. Тогда Р(А)=Р(А₁·А₂·А₃). События А₁, А₂ и А₃ – независимы, так как тот факт, что первый шар - черный - не влияет на цвет вынутого шара во 2-ой и 3-ий раз. Значит, Р(А)=Р(А₁·А₂·А₃)=Р(А₁)·Р(А₂)·Р(А₃)= · · = = .

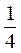Пример. Стрелок производит 3 выстрела по мишени. Вероятности попадания при первом, втором и третьем выстрелах соответственно равны 0,4, 0,5 и 0,7. Найти вероятности того, что в результате этих выстрелов окажется: а) одно попадание в мишень; б) хотя бы одно попадание.

Решение. а) Введем событие, вероятность которого надо найти: A={одно попадание в мишень}

По условию задачи известны вероятности попадания в мишень при первом, втором и третьем выстрелах. Введем соответствующие события:

A₁={попадание в 1 выстреле}, Р(А₁)=0,4

A₂={попадание во 2 выстреле}, Р(А₂)=0,5

A₃={попадание в 3 выстреле}, Р(А₃)=0,7

Выразим событие А через события A₁, A₂ и A₃: А= .

Тогда Р(А)=Р()=

события - несовместны, значит

= =

результат попадания стрелка в 1-ом выстреле не влияет на промах при 2-ом и 3-ем выстрелах, значит, события =

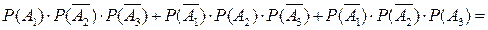
вычислим вероятности противоположных событий, присутствующих в выражении

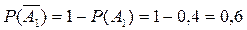
=0,4·0,5·0,3+0,6·0,5·0,3+0,6·0,5·0,7=0,36

б) Рассмотрим событие B={хотя бы одно попадание}. Проще вычислить вероятность этого события через противоположное событие 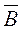={ни одного попадания}. Выразим событие 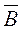через события A₁, A₂ и A₃ : 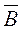= . Тогда Р(В)=1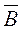-Р()=Р(). События - независимы, так как результат промаха стрелка в 1 выстреле не влияет на промах во 2 и 3 выстрелах.

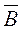Р(В)=1-Р()=1-Р()=1-Р()=1-0,6·0,5·0,3=

=0,91.

Пример. Студент пришел на зачет, зная ответы на 24 из 30 вопросов. Какова вероятность сдать зачет, если после первого отказа отвечать на вопрос преподаватель задает еще один вопрос?

Решение. 30 вопросов

24 вопроса – знает 6 вопросов – не знает

Введем событие А={зачет сдан}.

Выделим события: А₁={ответил на 1-ый вопрос}

А₂={ответил на 2-ой вопрос}

Выразим событие А через события A₁, A₂: А=А₁+ . События А₁ и одновременно произойти не могут, то есть являются несовместными.

Значит, Р(А)=Р(А₁+ )=Р(А₁)+Р()=(события - независимы)=Р(А₁)+Р(). Вычислим вероятности событий А₁, : Р(А₁)= , Р( =1-Р(А₁)=1- .

После того, как студент не ответил на 1-ый вопрос, у преподавателя остается набор из 29 вопросов, а значит Р(А₂)= .

Таким образом, Р(А)= Р(А₁)+Р()= .

Контрольные вопросы:

1. Чему равна вероятность достоверного события?

2. Чему равна вероятность суммы несовместных событий?

3. Чему равна вероятность противоположного события?

4. Чему равна вероятность невозможного события?

5. Назовите верхнюю и нижнюю границы вероятности любого события.

6. Сформулируйте аксиомы теории вероятностей.

Литература:

1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 471 с.

2. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. –М.: ИНФРА-М, 2006. – 655 с.

3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред.В.И. Ермакова. М.: ИНФРА-М, 2006. – 574 с.

4. Гмурман В. Е. Руководство к решению задач по теории вероятностей и магматической статистике. - М.: Высшая школа, 2005. – 400 с.

5. Гмурман. В.Е Теория вероятностей и математическая статистика. - М.: Высшая школа, 2005.

6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Оникс 21 век: Мир и образование, 2005. – 304 с. Ч. 1; – 416 с. Ч. 2.

7. Математика в экономике: Учебник: В 2-х ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандара. – М.: Финансы и статистика, 2006.

8. Шипачев В.С. Высшая математика: Учебник для студ. вузов – М.: Высшая школа, 2007. – 479 с.