Свойства вероятности

Методические указания к проведению лекционного занятия

Тема № 7.4. Свойства вероятности.

Аксиоматическое определение вероятности

План:

1. Свойства вероятности

2. Аксиоматическое определение вероятности

Свойства вероятности

1. Вероятность достоверного события равна 1, то есть Р(Ω)=1

Доказательство. Поскольку достоверное событие происходит всегда в ходе стохастического эксперимента, то число благоприятных исходов равно числу всех возможных исходов, а значит, в отношении получится 1.

2. Если события А и В – несовместны, то Р(А+В)=Р(А)+Р(В)

Доказательство. По определению, Р(А+В)= . Так как события А и В – несовместны, то есть одновременно произойти не могут в одном исходе эксперимента, то среди m благоприятных исходов для события А+В можно выделить m₁ исходов благоприятных А и m₂ исходов, благоприятных В. Тогда, Р(А+В)= =Р(А)+Р(В).

3. Вероятность противоположного события: Р()=1-Р(А)

Доказательство. Событие А и противоположное событие вместе составляют пространство всех исходов эксперимента, то есть достоверное событие. К тому же А и - несовместны, а значит, Р()=Р(А)+Р()=1, Р()=1-Р(А).

4. Вероятность невозможного события равна 0: Р(Ø)=0

Доказательство. Невозможное событие никогда не происходит в ходе стохастического эксперимента, то число благоприятных исходов равно 0. Значит, Р(Ø)=0

5. Вероятность любого события удовлетворяет условию: Р(А) [0;1]

Доказательство. Число благоприятных исходов событию А удовлетворяет условию 0 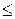m 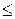n, где n - число всех возможных исходов эксперимента, тогда дробь находится в отрезке: 0 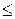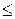1, то есть Р(А) [0;1]

Статистическое определение вероятности наряду с простотой и наглядностью имеет ряд недостатков: предусматривает конечное или счетное множество элементарных событий и обязательно знание их вероятностей. Все это не всегда имеет место, и поэтому введенное определение не является достаточно общим. В настоящее время стало общепринятым аксиоматическое построение теории вероятностей.