Біном Ньютона

Означення 10.1. Біном Ньютона – це формула для розкладу на окремі складові цілого невід’ємного ступеня суми двох змінних, що має вигляд:

Через цю властивість числа також називають біноміальними коефіцієнтами.

Розглянемо деякі властивості та тотожності біноміальних коефіцієнтів.

1. Правило симетрії. Нехай n і r – невід’ємні числа, . Тоді .

2. Рівність Паскаля:

Рівність Паскаля дає змогу побудувати трикутник Паскаля для коефіцієнтів .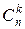

n =0

n =1

n =2

n =3

n =4

n =5

Приклад 10.1. Знайдемо розклад виразу (х +у)⁴. Скориставшись біноміальною теоремою, можемо записати:

= .

Біноміальні коефіцієнти з трикутника Паскаля співпадають з отриманим виразом. ▲

3. Винесення за дужки.

4. Заміна індексів.

5. Згортка Вандермонда. Нехай т, n, r — невід'ємні цілі числа, причому r 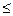min{ m, n }. Тоді .

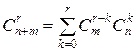6. Унімодальність. За фіксованого n послідовність біноміальних коефіцієнтів (C ),k=0,1,2…, n унімодальна, т = . У разі парного n максимум досягається в точці т = = , а в разі непарного — у двох точках: т = = й m +1= .

За допомогою біноміальної теореми можна виводити цікаві властивості біноміальних коефіцієнтів.

Приклад 10.2. Довести ,

Скористаємось формулою бінома Ньютона, підставивши x =1, y =1.

Скористаємось формулою бінома Ньютона, підставивши x =1, y =-1.

▲

Означення 10.2. Поліноміальна формула - цеформула для розкладу на окремі складові цілого невід’ємного ступеня суми кількох змінних, що має вигляд суми всіх можливих доданків де тобто

.

Поліноміальна формула є узагальненням Біному Ньютона, в чому можна переконатись, підставивши k =2 в поліноміальну формулу.

Задача про цілочислові розв'язки

Цю задачу формулюють так: знайти кількість розв'язків рівняння 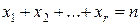у цілих невід'ємних числах, де п — ціле невід'ємне число.

Узявши такі невід'ємні цілі числа що можна одержати сполучення з повтореннями з r елементів по п, а саме: елементів першого типу — х ₁ одиниць, другого — х ₂ ,..., r- го — х_r. Навпаки, якщо є сполучення з повтореннями з r елементів по п, то кількість елементів кожного типу задовольняють вимоги рівняння у цілих невід'ємних числах. Отже, кількість цілих невід'ємних розв'язків цього рівняння дорівнює:

Приклад 11.1. Знайдемо кількість невід'ємних цілих розв'язків рівняння х ₁ +х ₂ +х ₃ = 10. Безпосереднє використання попередньої формули дає

▲

Кількість розв'язків рівняння x ₁+ х ₂ +...+х_r = п у цілих невід'ємних числах можна визначити й тоді, коли на змінні накладено певні обмеження.

Приклад 11.2. Знайдемо кількість невід'ємних цілих розв'язків рівняння

де

Зробимо заміну змінних:

Отримаємо рівняння:

отже, кількість цілочисельних розв’язків:

▲

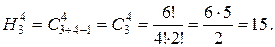Приклад 11.3. Визначимо кількість розв'язків нерівності в невід'ємних цілих числах. Уведемо допоміжну змінну х ₄, яка може набувати цілих невід'ємних значень, і перейдемо до еквівалентної задачі: визначити кількість розв'язків рівняння х ₁+ х ₂+ х ₃+ х ₄ = 10 в невід'ємних цілих числах. Отже, ▲