 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Обчислення кількості розміщень і сполучень
|
|
Нехай r і n — будь-які невід'ємні цілі числа. Кількість усіх розміщень без повторень з n елементів по r позначають як 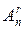 або A(n, r). Кількість різних розміщень із повтореннями з n елементів по r позначають як
або A(n, r). Кількість різних розміщень із повтореннями з n елементів по r позначають як 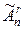 або
або 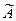 (n,r). Кількість усіх сполучень без повторень з n елементів по r позначають як
(n,r). Кількість усіх сполучень без повторень з n елементів по r позначають як  , С(n, r) або (
, С(n, r) або ( ). Кількість усіх сполучень із повтореннями з n елементів по r позначимо як
). Кількість усіх сполучень із повтореннями з n елементів по r позначимо як 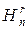 або Н(n, r). Очевидно, що для вибірок без повторень повинна виконуватись рівність r
або Н(n, r). Очевидно, що для вибірок без повторень повинна виконуватись рівність r 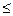 n, а для вибірок з повтореннями ця рівність не є обов’язковою.
n, а для вибірок з повтореннями ця рівність не є обов’язковою.
ТЕОРЕМА 7.1. Кількість усіх розміщень без повторень з n елементів по r рівна 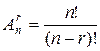 .
.
Доведення. Розглянемо алгоритм отримання вибірки. Нехай задано скінченну непорожню множину А = {а1, а2,… аn} і виконано r таких кроків.
Крок 1. Із множини А вибирають якийсь елемент 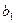 . Цей елемент можна отримати n способами, бо у множині А є n елементів.
. Цей елемент можна отримати n способами, бо у множині А є n елементів.
Крок 2. Із множини A чи з 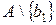 вибирають якийсь елемент
вибирають якийсь елемент 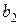 . Цей елемент можна отримати n-1 способами, бо у множині
. Цей елемент можна отримати n-1 способами, бо у множині 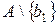 є n-1 елемент.
є n-1 елемент.
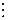
Крок r. Якщо 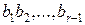 — елементи, які вибрані на перших r - 1 кроках (r >= 3), то на цьому кроці вибирають якийсь елемент
— елементи, які вибрані на перших r - 1 кроках (r >= 3), то на цьому кроці вибирають якийсь елемент 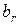 із множини А чи
із множини А чи 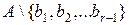 . Цей елемент можна отримати n-r+1 способом.
. Цей елемент можна отримати n-r+1 способом.
Елементи 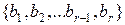 утворюють вибірку обсягом r, або r-вибірку із множини А. Використавши правило добутку, отримаємо, що кількість способів отримання такої вибірки є n(n-1)(n-2)…(n-r+1). ▲
утворюють вибірку обсягом r, або r-вибірку із множини А. Використавши правило добутку, отримаємо, що кількість способів отримання такої вибірки є n(n-1)(n-2)…(n-r+1). ▲
ТЕОРЕМА 7.2. Кількість різних розміщень із повтореннями з n елементів по r рівна 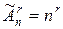 .
.
Доведення. Рівність доводиться аналогічним способом, як у попередній теоремі. Легко побачити, що в розміщенні з повтореннями  для кожного елемента bi, і=1,2,…,r є n незалежних можливостей вибору, тому згідно правила добутку
для кожного елемента bi, і=1,2,…,r є n незалежних можливостей вибору, тому згідно правила добутку 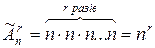 .▲
.▲
ТЕОРЕМА 7.3. Кількість усіх сполучень без повторень з n елементів по r рівна 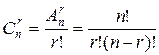 .
.
Доведення. Розглянемо всі розміщення без повторень з n елементів по r (b1,b2,…br) і всі сполучення [b1,b2,…br] без повторень з n елементів по r. Виявимо, у скільки разів більше сполучень ніж розміщень. Для цього визначимо, скільки можна отримати розміщень із одного сполучення [b1,b2,…br] шляхом різних перестановок елементів. Легко побачити, що впорядкувати r елементів можна 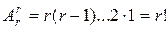 способами, бо перший елемент можна вибрати r способами, другий r-1 способом і т.д. Очевидно, що із двох різних сполучень без повторень не можна одержати однакових розміщень без повторень. Отже, всіх розміщень з n елементів по r у
способами, бо перший елемент можна вибрати r способами, другий r-1 способом і т.д. Очевидно, що із двох різних сполучень без повторень не можна одержати однакових розміщень без повторень. Отже, всіх розміщень з n елементів по r у 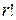 разів більше, ніж сполучень з n елементів по r
разів більше, ніж сполучень з n елементів по r
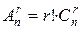
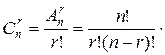 ▲
▲
ТЕОРЕМА 7.4. Кількість усіх сполучень із повтореннями з n елементів по r рівна 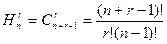 .
.
Доведення. Розглянемо множину А = { 1,2,…,n } з n елементів. Кожну невпорядковану r -вибірку з множини А можна записати у вигляді [ m1,m2,…,mr ], де 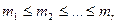 , оскільки порядок елементів не суттєвий. Тоді [ m1+0, m2+1,…, mr+r-1 ] — сполучення без повторень з n + r - 1 елементів по r.
, оскільки порядок елементів не суттєвий. Тоді [ m1+0, m2+1,…, mr+r-1 ] — сполучення без повторень з n + r - 1 елементів по r.
Легко переконатись, що кожному сполученню [ m1+0, m2+1,…, mr+r-1 ] без повторень з n+r-1 елементів по r відповідає, до того ж тільки одне, сполучення [ m1,m2,…,mr ] із повторенням з n елементів по r.
Отже, кількість сполучень із повторенням з n елементів по r рівна кількості сполучень без повторень з n+r-1 елементів по r. 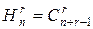 .Рівність доведено. ▲
.Рівність доведено. ▲
Значення вищеописаних кількостей у вибірках зручно представити таблицею.
Таблиця 3.1. Кількість елементів у вибірці
| Без повторень | З повтореннями | |
| Розміщення | 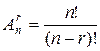
| 
|
| Сполучення | 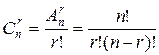
| 
|
Дата публикования: 2015-09-17; Прочитано: 1235 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
