Графічна інтерпретація розв’язання задач ЛП

Геометрична інтерпретація дає можливість наочно зобразити структуру задач ЛП, що сприяє засвоєнню їх основних властивостей. У найпростіших випадках одно- і двовимірного просторів геометричне зображення дає змогу знайти розв’язання задачі ЛП у стандартній формі якнайзручнішим способом. Також, матимемо на увазі, що геометричну інтерпретацію задачі можна задати у канонічній формі з числом незалежних невідомих та задачі у загальній формі запису, яка може бути зведена до канонічної форми запису. Розглянемо таку задачу.

Знайти екстремум лінійної форми (2.1) за умови обмежень (2.2) - (2.3), при цьому у цих виразах покладемо, що n =2. Кожна із нерівностей системи обмежень визначає півплощину, що обмежується прямою a_i1x₁+a_i2x₂=b_i, (). Умови невід’ємності шуканих змінних визначають півплощини відповідно з граничними прямими x₁=0, x₂=0.

Якщо система обмежень сумісна, то переріз півплощин як опуклих множин, утворить опуклу множину точок, координати якої є розв’язками системи рівнянь обмежень. Сукупність цих точок і буде множиною планів або допустимих розв’язків. Лінійну форму на площині можна інтерпретувати як сім’ю деяких паралельних прямих, кожна з яких визначається значенням цільової функції.

Якщо f = 0, пряма проходить через початок координат. Інші значення цільової функції є відстанню даної прямої від початку координат помноженою на довжину вектора С= (с₁, с₂), координатами якого є коефіцієнти при змінних лінійної форми. Нас цікавлять лише ті прямі, які відповідають лінійній формі, що мають спільні точки із сторонами багатокутника роз­в’язків. При цьому задача ЛП полягає у тому, щоб, зміщуючи пряму лінійної форми, знайти спільну з нею таку точку багатокутника розв’язків, в якій лінійна форма приймає екстремальне значення. Напрям руху прямої цільової функції визначається вектором С= (с₁,с₂). Під час зміщення прямої лінійної форми в його напрямку значення цільової функції зростає, а під час переміщення у протилежному напрямку – спадає.

В усіх випадках екстремальні значення цільової функції досягаються на межі множини планів (пряма лінійної форми дотикається до багатокутника розв’язків у граничних точках) і визначення екстремальних значень лінійної форми зводиться до порівняння їх у граничних точках багатокутника, заданих обмеженнями. При цьому можливі такі випадки.

1. Багатокутник планів задачі ЛП обмежений, при цьому лінійна форма досягає екстремуму або в окремих вершинах багатокутника, або на деякій грані або на ребрі, якщо гіперплощини рівні паралельним граням.

2. Багатокутник планів задачі ЛП є необмеженим. Тоді лінійна форма може бу­ти необмеженою на множині планів лише знизу або лише зверху, або і знизу, і зверху.

3. Множина планів задачі ЛП порожня, тобто не існує багатокутника існу­вання планів, які б не суперечили системі обмежень.

Зауваження. Для будь-якої розмірності вектора шуканих змінних канонічної форми, розмірність багатокутника планів завжди визначається числом незалежних змінних, тобто різницею між кількістю залежних змінних і рангом системи обмежень: k = n – m, m = r.

Алгоритм геометричної інтерпретації задач ЛП з двома основними змінними містить такі етапи.

1. У кожному обмеженні, що задане нерівністю, замінити знаки нерівностей на знаки рівнянь і провести на площині відповідні їм прямі.

2. Знайти півпростір, заданий відповідним обмеженням – нерівні­стю.

3. Виявити багатокутник планів задачі.

4. Провести гіперплощину – пряму рівня цільової функції, щомає спільні точки з багатокутником планів.

5. Визначити напрям зміщення прямої рівня цільової функції для досягнення екстремуму.

6. Знайти точку (або точки) багатокутника, де пряма рівня досягає екстремуму або встановити її необмеженість на множині планів задачі.

7. Знайти координати точки розв’язку задачі ЛП, що і буде оптимальним планом задачі.

Приклад 2.3. (Випадок єдиного оптимального розв’язку). Викори­сто­вуючи графічний метод, знайти розв’язок такої задачі ЛП:

max f (x) = x₁- x₂;

3х₁+2х₂ ≤ 14;

x₁ – 4x₂ ≤ 0;

3x₁ – x₂ ≥ 0;

–x₁ + x₂ ≤ 2;

x₁ ≥ 0, x₂ ≥ 0.

Розв’язування. На площині R² будуємо допустиму множину, що описується шістьма нерівностями. Це буде перерізання шести півплощин, кожна з яких задається обмеженням – нерівністю на R². Наприклад, першу з них 3x₁+2х₂ ≤ 14 будуємо таким чином. Проводимо пряму 3x₁+2х₂ = 14, що є межею цієї півплощини. Щоб визначити, яку з півплощин, що лежать з обох сторін від цієї прямої, описує нерівність 3x₁+2х₂ ≤ 14, досить поставити в ній координати початку координат, тобто (0,0). Якщо нерівність виконується, то беремо ту півплощину, що містить початок координат, якщо не виконується, то беремо півплощину, що не містить початку координат. У нашому випадку 3х0 + 2х0 ≤ 14.

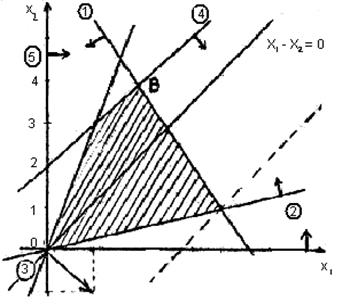
На рисунку нижче у кружках написані номери ліній (меж півплощин), а півплощини позначені стрілками. У результаті перерізання побудова­них шести півплощин отримуємо багатокутник ОАВС, що і є допустимою множиною даної задачі. Можна перевірити, що будь-яка точка у ньому задовольняє усі шість нерівностей, а для будь-якої точки поза цим багатокутником хоча б одна з цих нерівностейбуде порушена.

Таким чином, геометрично задача звелася до того, щоб у межах багатокутника ОАВС знайти точку х* = (x₁*, x₂*), у якій цільова функція f (x*) отримає максимальне значення.

Завдяки властивості 1.3 ми заздалегідь знаємо, що точкою максимуму нашої цільової функції є одна або деякі з вершин О,А,У або С. Для того, щоб визначити цю вершину, проведемо будь-яку лінію рівня цільової функції, тобто проведемо пряму f (x) = с ₁, де с= const. Для простоти візьмемо с =0, тоді лінія рівня є x₁-x₂ = 0. Збільшуючи праву частину цього рівняння (наприклад, x₁-x₂ = 1, x₁-x₂ = 3 і т.д.), ми знайдемо паралельний зсув лінії рівня вниз, причому, чим більша права частина, тим більший зсув. Якщо ж зменшимо праву частину (наприклад, x₁ - x₂ = -1, x₁ - x₂ = - 2 і т.д.), то спостерігаємо зсув уверх.

Звідси зрозуміло, що зміщаючи лінію рівня у напрямку зростання цільової функції, ми знайдемо ту вершину багатокутника ОАВС, що відповідає точці максимуму. Як видно з вищенаведеного рисунка, це є точка С.

Щоб відразу визначити напрямок зростання функції t, обчислюють її градієнт Ñ f. Для лінійної функції градієнт завжди дорівнює вектору, що складається з коефіцієнтів цієї функції.

Для нашої цільової функції f (x) = x₁-x₂ градієнт Ñ f = (1,-1). Як відомо, градієнт, що перпендикулярний лінії рівня, показує напрямок зростання функції, а антиградієнт, тобто вектор -Ñ f, показує напрямок убування функції. Отже, зміщуючи лінію рівня x₁-x₂ =0 у напрямку вектора Ñ f, знаходимо точку максимуму С.

Координати точки С знайдемо розв’язуючи спільно рівняння ліній 1 і 2, що перетинаються у точці 3: 3 x ₁+2 x ₂ = 14; x ₁-4 x ₂ = 0/

Відповідь: х* = (4, 1) – точка максимуму, f (x*) = 3 – максимальне значення цільової функції.

Приклад 2.2. (Нескінченна множина оптимальних розв’язків):

min f (x) = - x 1-2 x 2

за обмежень

x₁+ 2 x₂ ≤ 7;

2x₁ + x₂ ≤ 8;

x₂ ≤ 3;

x₁, x₂ ≥ 0.

Як видно з рисунка зліва найвлучнішим вбік антиградієнти – f = (1,2) місцем дотику лінії рівня f (x) = с з допустимою множиною OABCD є грань ВС (тобто опуклість вершин B = (l, 3) і С = (3,2). Тому будь-яка точка грані ВС є точкою мінімуму цільової функції.

Відповідь: х* = a (1,3)+(1- a)(3,2) = (3-2 a, 2+ a) для кожного a Î[0, 1] - точка мінімуму, f (x*) = -7 - мінімальне значення цільової функції.

Приклад 2.3. (Випадок відсутності оптимуму через не­об­ме­же­ність цільової функції на допустимій множині):

min f (x) = - x₁ -2 x₂

за обмежень:

x1+x2 ³ 1; 2 x1-x2 ³ -1; x1 -2 x2 ≤ 0; x1, x2 ≥ 0.

Допустима множина цієї задачі являє собою необмежений багатокутник (див. на рисунку зверху). При паралельному переносі лінії рівня f (x) = с уздовж антиградієнта -Ñ f = (1,2) вона завжди перетинає допустиму множину, тобто немає найвіддаленішої точки дотику, а цільова функція нескінченно спадає.

Відповідь: Точки мінімуму немає; цільова функція не обмежена знизу.

Приклад 2.4. (Випадок відсутності оптимального розв’язку через порожнечу припустимої множини B):

max f (x) = x₁+x₂

за обмежень:

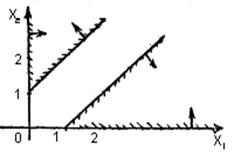-x₁+x₂ ≤ -1;

-x₁-x₂ ≤ -1;

x₁, x₂ ≥ 0.

Як показано на рисунку зліва, півплощини, що утворені першими двома нерівностями, не перетинаються і тому система несумісна, тобто немає ні однієї допустимої точки.