Кручение

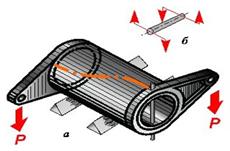
Схема нагружения кручением показана на рис. 10.18, б. Внешние силы, образующие момент относительно оси элемента конструкции, вызывают его деформации, которые заключаются в плоском повороте поперечных сечений друг относительно друга. Продольная линия, нанесенная на поверхность элемента конструкции, нагруженного кручением (рис. 10.18, а), принимает форму винтовой.

Рис. 10.18. Нагружение кручением

В любом поперечном сечении круглого стержня (рис. 10.19, а) при скручивании точка А на его поверхности стремится занять положение, отмеченное точкой А', а точка Б - положение Б'. Этому перемещению будут препятствовать внутренние силы - касательные напряжения (напряжения сдвига) τ, направленные вдоль кольцевых линий. Очевидно, что напряжения по сечению распределятся неравномерно (рис. 10.19, б). Они максимальны в крайних точках и снижаются до нуля на осевой линии. Несущая способность сплошного стержня используется не полностью (в центре материал недогружен).
Наиболее рациональным конструктивным элементом, предназначенным для восприятия кручения, является тонкостенная оболочка, по толщине которой (рис. 10.19, в) напряжения τ распределены практически равномерно.

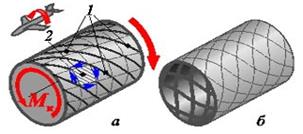
Однако нагружение кручением тонкостенной оболочки (рис. 10.20, а) может привести к потере устойчивости с образованием равномерно расположенных в окружном направлении вмятин, идущих от одного торца к другому по винтовым линиям 1.

	Рис. 10.19. Напряжения при кручении	Рис. 10.20. Кручение тонкостенной оболочки
Сравните схему работы клетки 2 (заштрихованного элемента на рис.10.20,а) со схемой, изображенной на рис.10.17.

Для повышения несущей способности такой оболочки ее необходимо подкреплять в направлении возможной потери устойчивости (подкрепление геодезического типа - рис. 10.20, б). Из технологических соображений подкрепление чаще ведется в продольном и поперечном направлениях (как на рис. 10.14), т. е. окантовывается клетка 2

(рис. 10.20, а), подверженная сдвигу при кручении.

Изгиб

Схема нагружения изгибом показана на рис. 10.21, а. Внешние силы, образующие момент относительно оси с-с, перпендикулярной продольной оси балки, вызывают деформации, которые заключаются в искривлении продольной оси балки. Такой вид деформированного состояния называют чистым изгибом.
В технике широко распространен изгиб элементов конструкции, вызванный приложением к ним сосредоточенной силы или распределенной нагрузки (см. раздел 8.1, рис. 8.1-8.8).

Рис. 10.21. Изгиб балки прямоугольного сечения	Рис. 10.22. Уравновешивание балки при поперечной нагрузке

Для простейшей балки прямоугольного сечения (рис. 10.21, б), нагруженной сосредоточенной силой, деформированное состояние характеризуется наличием нормальных σ и касательных τ напряжений в любом поперечном сечении. Выпуклая сторона балки растянута, вогнутая - сжата. Зоны растяжения и сжатия разделены нейтральным слоем, длина которого при изгибе остается неизменной и нормальные напряжения в котором отсутствуют.
Статическое равновесие балки под поперечной нагрузкой обеспечивают нормальные напряжения σ, создающие уравновешивающий момент М, и касательные напряжения τ, создающие уравновешивающую перерезывающую силу Q. Это можно проследить, рассматривая равновесие по сечению А-А (рис. 10.22) консольной балки 1, заделанной на опору 2.
Как и в случае с кручением (см. рис. 10.19, в), сплошное поперечное сечение конструктивного элемента, работающего на изгиб, нерационально, так как вблизи нейтрального слоя материал недогружен.
Наиболее рациональным будет сечение (рис. 10.23), в котором основная масса материала сосредоточена в зонах, максимально удаленных от нейтральной оси, - в поясах 1 и 4, которые, работая на растяжение (пояс 1) и сжатие (пояс 4), создают уравновешивающий изгибающий момент М _изг. Тонкая стенка 2, соединяющая пояса и подкрепленная стойками 3, работая на сдвиг, создает уравновешивающую перерезывающую силу Р.
Различные внешние нагрузки, которые одновременно действуют на ЛА, стремясь деформировать и, в пределе, разрушить конструкцию, создают в ней весь спектр внутренних сил.

Так, (рис. 10.24) под действием распределенных воздушной q _возд и массовой q _мас нагрузок и сосредоточенных сил тяги Р _дв и веса G _дв двигателя в любом произвольно взятом сечении крыла (например, плоскостью А) возникнут внутренние силовые факторы: перерезывающая сила Q, изгибающий М _изг и крутящий М _кр моменты, которые будут уравновешивать условно отсеченную (концевую) часть крыла 1. Равные им, но противоположные по направлению силовые факторы для оставшейся (внутренней) части крыла 2 будут являться внешними нагрузками, заменяя отсеченную часть крыла.

Рис. 10.23. Тонкостенная балка	Рис. 10.24. Уравновешивание крыла

В первом приближении можно не учитывать напряженно-деформированное состояние крыла под действием силы лобового сопротивления Х и силы тяги двигателя Р _дв, стремящихся изогнуть конструкцию крыла в плоскости хорд, поскольку очевидно, что жесткость на изгиб крыла в этом направлении значительно больше, чем жесткость на изгиб "из плоскости" (в вертикальном направлении). Кроме того, силы, действующие на крыло в горизонтальной плоскости, значительно меньше.
Напомним, что в горизонтальном установившемся полете