 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Способи задання множин
|
|
1. Перелік елементів – найбільш природний спосіб задання множини, коли множина 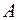 , яка складається з елементів
, яка складається з елементів 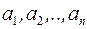 , задається списком своїх елементів:
, задається списком своїх елементів:  , де порядок слідування елементів значення не має.
, де порядок слідування елементів значення не має.
Наприклад: 
 .
.
Вважається, що всі елементи множини різні.
2. За допомогою характеристичної властивості елементів – універсальний спосіб задання множини, коли властивості її елементів можуть бути описані виразом  (елементи
(елементи 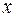 даної множини і тільки вони мають властивість
даної множини і тільки вони мають властивість  ). Записують
). Записують  . Наприклад:
. Наприклад: 
3. Аналітичний, за допомогою символів операцій над множинами та дужок (буде розглянуто нижче).
3. Відношення між множинами. Геометричне зображення множин
Означення. Множина 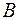 називається підмножиною множини
називається підмножиною множини 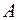 , якщо кожен елемент множини
, якщо кожен елемент множини 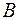 належить множині
належить множині 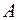 .
.
Позначення:  (
( ) – «
) – «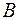 включається в
включається в 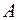 » (
» (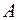 включає
включає 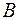 ), де
), де  – знак нестрогого включення.
– знак нестрогого включення.
 .
.
Наприклад:  ,
, 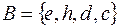 ,
,  –
– 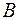 – підмножина
– підмножина 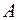 .
.
Означення. Множини 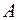 і
і 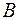 називаються рівними, якщо вони складаються з одних і тих самих елементів, тобто
називаються рівними, якщо вони складаються з одних і тих самих елементів, тобто  і
і  .
.
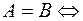
 і
і  .
.
Якщо  и
и  , то
, то 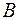 називається власною, строгою чи істинною підмножиною
називається власною, строгою чи істинною підмножиною 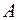 . Позначення:
. Позначення:  , де
, де  – знак строгого включення.
– знак строгого включення.
Очевидно, що для будь-якої множини 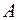
 і
і  .
.
 і
і 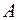 називаються невласними підмножинами множини
називаються невласними підмножинами множини 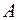 .
.
Для кожної множини 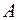 існує множина, елементами якої є всі її підмножини.
існує множина, елементами якої є всі її підмножини.
Означення. Множина, елементами якої є всі підмножини множини 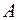 і тільки вони, називається булеаном (або множиною підмножин) множини
і тільки вони, називається булеаном (або множиною підмножин) множини 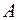 і позначається
і позначається  . Відносно елементів булеана множина
. Відносно елементів булеана множина 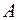 є універсумом. (Тобто, універсальна множина – це множина, підмножинами якої є всі множини, що розглядаються,)
є універсумом. (Тобто, універсальна множина – це множина, підмножинами якої є всі множини, що розглядаються,)
У разі скінченної підмножини 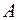 , що складається з
, що складається з  елементів, булеан
елементів, булеан  містить
містить  елементів:
елементів:
 .
.
Приклад. Якщо  , то
, то  . Перша й остання підмножини невласні, інші – власні.
. Перша й остання підмножини невласні, інші – власні.
 має властивість:
має властивість:  при будь-якому
при будь-якому 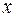 . Універсальна множина
. Універсальна множина  має властивість:
має властивість:  при будь-якому
при будь-якому 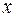 .Множини і відношення між ними зручно задавати графічно за допомогою так званих діаграм Ейлера-Венна. Діаграми Ейлера-Венна є геометричним зображенням множин. Множина зображується замкненою кривою довільної форми (найчастіше – кругом). Точки, які лежать всередині замкненої кривої, можна розглядати як елементи відповідної множини.
.Множини і відношення між ними зручно задавати графічно за допомогою так званих діаграм Ейлера-Венна. Діаграми Ейлера-Венна є геометричним зображенням множин. Множина зображується замкненою кривою довільної форми (найчастіше – кругом). Точки, які лежать всередині замкненої кривої, можна розглядати як елементи відповідної множини. Наприклад:


Універсум  на діаграмах Ейлера-Венна зображується у вигляді прямокутника.
на діаграмах Ейлера-Венна зображується у вигляді прямокутника.

3. Основні операції над множинами
Існує ще один спосіб задання множин – за допомогою операцій над іншими множинами. На булеані  визначаються наступні операції над множинами
визначаються наступні операції над множинами  і
і  .
.
| Назва і позначення | Означення | Геометрична ілюстрація |
Об'єднання 
| 
| 
|
Переріз 
| 
| 
|
Різниця 
| 
| 
|
Доповнення

| 
| 
|
Симетрична різниця

| 
| 
|
 ¸ \¸
¸ \¸  можна виражати одні множини через інші. За умовчанням приймається пріоритет операцій:
можна виражати одні множини через інші. За умовчанням приймається пріоритет операцій:  . Для зміни цього порядку у виразі використовують дужки.
. Для зміни цього порядку у виразі використовують дужки. Таким чином, множину можна задати виразом, в який входять множини, операції і, може бути, дужки. Такий спосіб завдання множини називається аналітичним.
4. Властивості операцій над множинами
Операції над множинами, як і операції над числами, мають певні властивості. Ці властивості виражаються сукупністю тотожностей незалежно від конкретного змісту множин, що входять у них, і є підмножинами деякого універсуму  , тобто множинами з
, тобто множинами з  .
.
Теорема. Для будь-яких множин 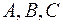 з булеану
з булеану  справедливі наступні тотожності (основні закони теорії множин):
справедливі наступні тотожності (основні закони теорії множин):
1.  – комутативність – комутативність 
| 1*.  – комутативність – комутативність 
|
2.  –
асоціативність –
асоціативність 
| 2*.  – асоціативність – асоціативність 
|
3.  – дистрибутивність – дистрибутивність  відносно відносно 
| 3*.  – дистрибутивність – дистрибутивність  відносно відносно 
|
| закони поглинання | |
4. 
| 4*. 
|
| закони де Моргана | |
5. 
| 5*. 
|
6. 
| |
| закони ідемпотентності | |
7. 
| 7*. 
|
властивості  і і 
| |
8. 

| 8*. 

|
9. 
| 9*. 
|
10.  , , 
| |
11. 
| |
12. 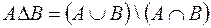
|
Доведення (самостійно) всіх рівносильностей проводиться
1) за означенням рівності множин і за означеннями операцій над множинами.
2) за допомогою діаграм Ейлера-Венна.
За допомогою основних властивостей операцій над множинами доводять рівності множин і спрощують вирази алгебри множин.
Дата публикования: 2015-09-18; Прочитано: 7951 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
