Модель оценки разведзащищенности сети связи

В качестве математической модели сети выберем вероятностно взвешеный граф, вершинам которого соответствуют узлы и комплексы связи, а ребрам- каналы связи, их соединяющие.

В качестве весовых коэффициентов вершин используются накопленные к заданному времени вероятности обнаружения единичных сообщений, исходящих из узла, соответствующего данной вершине.

(1)

где Р_i (t)-накопленная вероятность обнаружения i-го объекта (узла);

r_i- число излучающих средств на i- м объекте;

l_ij(t)- интенсивность передач от i-го к j-ому объекту (узлу);

р₁(t)- вероятность обнаружения единичного сообщения, в общем случае зависящая от времени (места, дистанции, условий, диапазона работы i-го средства r_iи.т.д).

Распознавание структуры сводится к отнесению конкретно наблюдаемой сети к одному из заранее известных эталонов.

В качестве эталонов используется набор типовых структур, применяемых в системах связи и АСУ, каждая структура задается детерминированным графом-эталоном.

Для определения влияния только структурных свойств, индивидуальные демаскирующие признаки объектов, определяющие вероятность их распознавания, здесь учитывать не будем, поскольку это существенно упрощает задачу.

Для оценки структурной скрытности сети используется показатель- вероятность распознавания структуры сети к заданному моменту времени при заданной интенсивности обмена сообщениями l_ij(t) в заданных условиях ведения разведки, определяемых вероятностью обнаружения единичного сообщения р₁(t).

Процесс обнаружения будем рассматривать как обобщенный, позволяющий установить факт передачи сообщения и адресат, если он не скрывается, либо установить, что адресат скрывается, т.е. принимаются специальные меры по скрытию структуры сети.

Для получения численного значения показателя используется имитационная модель.

Обобщенный моделирующий алгоритм приведен на рис.4.1.

Блок 1- ввод исходных данных:

матрицы эталонов ||A||, размерности [nxn];

матрицы интенсивностей исследуемой структуры ||l_ij||;

способов организации: а_j =1 адресат j не скрывается, а_j =0 адресат скрывается;

характеристик радиоразведки р₁(t);

общего числа реализаций N^* на шаге моделирования;

шага моделирования Δt.

Блок 2. Вычисление текущих значений накопленных вероятностей для каждого i-го узла.

Блок 3. Розыгрыш графа- реализации по текущему значению Р_i (t) с учетом <а_j>.

Блок 4. Определение принадлежности графа-реализации к одному из графов-эталонов.

Блок 5. Расчет показателя структурной скрытности: 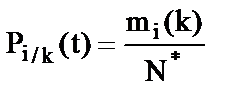, где m_i(k) - число случаев, когда граф-реализация относится к i-му эталону при фактическом розыгрыше k-го эталона.

Блок 6. Вывод результатов в виде зависимости вероятности распознавания от времени.

Таким образом P_{i/ k}(t) при i≠k характеризует эффективность маскировки, т.е. вероятность распознавания k-ой структуры как i-й, а при i=k как вероятность правильного распознавания k-ой структуры.

Рис.1. Блок-схема алгоритма оценки структурной скрытности.

Центральным в алгоритме является блок распознавания изоморфности (изоморфного вложения) графа реализации и графа- эталона, поэтому алгоритмы распознавания изоморфности рассмотрим более детально.

3. Алгоритмы распознавания изоморфности графов.

В методе распознавания деятельности по работе связи применен алгоритм распознавания случайных структур, позволяющий ускорить процесс распознавания структуры за счет информации о распознавании вершин (объектов). Однако этот алгоритм не позволяет отделить структурную составляющую скрытности от неструктурной, определяемой вероятностью распознавания вершин, а следовательно не позволяет сравнивать скрытность “чистых” структур, выявлять наиболее скрытные, а также параметры чистых структур, от которых зависит их скрытность. Именно с целью устранения этих недостатков метода были предложены алгоритмы распознавания изоморфности графов и определены условия их наиболее эффективного применения.

Здесь рассматривается способ, основанный на теореме о том, что в изоморфных графах циклы одного графа соответствуют циклам другого.

При таком способе используется не только информация о совпадении полустепей исхода и захода, но и о порядке следования вершин в цикле.

Если графы содержат по одному гамильтонову циклу, то задача решается практически за одну проверку, если графы содержат по одной вершине, отличающейся от всех остальных, и максимум за N проверок, если все вершины однородны. При отсутствии гамильтоновых циклов и большом количестве простых циклов, количество операций переборов подстановок вершин и проверок сохранения отношения смежности существенно возрастает. Этим определяется условие применения этого алгоритма.

Обобщенный алгоритм распознавания изоморфности графов представлен на рис.2. Пример приведен для графов, представленных на рис.3.

Задача формулируется следующим образом:

Имеются матрицы смежности графа- эталона и графа- реализации.

Требуется найти подстановки между вершинами графа-эталона и графа – реализации, сохраняющие отношения смежности или доказать обратное.

Матрицы смежностей имеют размерности (n,n), где n- число вершин

Задача решается следующим образом:

1. Вводятся матрицы графов-эталонов и реализации размерностью nxn:

А(n,n)-матрица смежности графа- эталона

В(n,n)-матрица смежности графа- реализации

Перечисляются возможные пути(циклы) в каждом графе. Результаты сохраняются в матрицах СЕ(s,n), CR(s,n) соответственно для обоих графов где s- число путей(циклов) в графе. Нахождение путей осуществляется методом прямого поиска в глубину;

3. Определяются составные степени каждой вершины в графах. Результаты сохраняются в e(n) для графа-эталона и f(n) для графа реализации.

4. Вычисляется число вершин в каждом пути (цикле) в матрицах CE(s,n), CR(s,n) и результаты сохраняются в матрицах К1(n), K2(n) соответственно.

Рис.2. Обобщенный алгоритм определения изоморфности графов

5. Сравнивается число вершин в каждом пути(цикле) графа-эталона с графом-реализацией. В случае равенства числа вершин, проверяется равенство их степеней. В противном случае проверяется следующий путь (цикл). При отсутствии такого равенства принимается решение “графы не изоморфны”.

6.В генерируемой матрице смежности добавляются единицы в соответствии с вершинами исследуемых циклов.

Проверка удовлетворения условия равенства степеней и сохранения смежности вершин, не вошедщих в циклы, в противном случае выполнять 5.

В случае выполнения пункта 7 добавлять соответственно к тем вершинам единицы в матрицу смежности.

9. получение перестановочной матрицы, в каждой строке и столбце которой содержится одна единица, т.е. элементы строк - это вершины графа-эталона, а элементы столбцов - соответствующие им вершины графа-реализации. Рассмотрим пример реализации алгоритма “вручную” и на ЭВМ.

a) б)

Рис.4.3. Исследуемые графы а)граф G(X,F), б) граф H(Y,P)

Пусть заданы два графа G(X,F) и H(Y,P), изображенных на рис.4.3.(а, б).

Задача – определить, являются ли они изоморфными.

При производстве перебора подстановок понадобятся некоторые структурные характеристики обоих графов.

Эти характеристики приведены в таблице(4.1)

Известна формула Эйлера для определения числа независимых циклов в связном графе M=B-N+1, (4.2)

где M-количество независимых циклов;

N- количество вершин в графе

B- количество ребер(ветвей) в графе.

Граф G(X,F)

Граф H(Y,P)

Вершины

Степени

Смежные Вершины

Вершины

Степени

Смежные вершины

X1

X2

X3

X4

Y1

Y2

Y3

Y4

X2

X1

X9

Y2

Y1

Y5

X3

X1

X6

Y3

Y1

Y9

X4

X1

X8

Y4

Y1

Y7

X5

X6

X9

Y5

Y2

Y6

Y8

X6

X3

X5

X7

Y6

Y5

Y7

X7

X6

X8

Y7

Y4

Y6

Y10

X8

X4

X7

X10

Y8

Y5

Y9

X9

X2

X5

X10

Y9

Y3

Y8

Y10

X10

X8

X10

Y10

Y7

Y9

В графах G(X,F) и H(Y,P) таких независимых циклов 3, например:

x₁ x₂ x₉ x₅ x₆ x₃ x₁ y₁ y₂ y₅ y₆ y₇ y₄ y₁

x₁ x₃ x₆ x₇ x₈ x₄ x₁ y₁ y₃ y₉ y₁₀ y₇ y₄ y₁

x₅ x₉ x₁₀ x₈ x₇ x₆ x₅ y₅ y₈ y₉ y₁₀ y₇ y₆ y₅

Идентифицируем 1 цикл графа G(X,F) с одним из циклов графа H(Y,P), используя соответственно отображения F и P.

Подстановки, входящие и не входящие в циклы, разделены вертикальной чертой:

x₁ x₂ x₉ x₅ x₆ x₃ x₄ x₇ x₈ x₁₀

y₁ y₂ y₅ y₆ y₇ y₄y₃ y₁₀ y₉ y₈ (3)

x₁y₁ →F(x₁) = {x₂, x₃, x₄ },P(y₁) ={y₂,y₃,y₄}⇒x₂y₂, x₃y₄ входят в подстановку (4.3),а x₄y₃ добавляем к ней

x₂y₂ → F(x₂) = {x₁, x₉},P(y₂) ={y₁,y₅}→x₁y₁,x₉y₅ входят в подстановку(3)

x₅y₆ →F(x₅) = {x₉, x₆},P(y₆) ={y₅,y₇}→x₉y₅, x₆y₇ входят в подстановку(3)x₆y₇→F(x₆) = {x₃, x₅, x₇ },P(y₁) ={y₄,y₆,y₁₀}→ x₃y₄, x₅y₆ входят в подстановку (3)а x₇y₁₀ добавляем к ней

x₃y₄→F(x₃) = {x₁, x₆},P(y₄) ={y₁,y₇}→ x₁y₁, x₆y₇ входят в подстановку (3)

x₄y₃→F(x₄) = {x₁, x₈},P(y₃) ={y₁,y₉}→ x₁y₁ входят в подстановку (3),а x₈y₉ добавляем к ней

x₇y₁₀ →F(x₇) = {x₆, x₈},P(y₁₀) ={y₇,y₉}→ x₆y₇, x₈y₉ входят в подстановку (3)

x₈y₉→F(x₈) = {x₄, x₇, x₁₀ },P(y₉) ={y₃,y₈,y₁₀}→x₄y₃, x₇y₁₀ входят в подстановку (3),а x₁₀y₈ добавляем к ней. Окончательно имеем подстановку:

x₁y₁, x₂y₂,x₃y₄, x₄y₃, x₅y₆, x₆y₇, x₇y₁₀, x₈y₉, x₉y₅, x₁₀y₈, которая удовлетворяет условию сохранеия смежности.

Рассмотрим подстановку по 2^-ым циклам:

x₁ x₃ x₆ x₇ x₈ x₄ x₂ x₅ x₁₀ x₉

y₁ y₂ y₅ y₆ y₇ y₄y₂ y₈ y₆ y₅ (4)

x₁y₁ →F(x₁) = {x₂, x₃, x₄ },P(y₁) ={y₂,y₃,y₄}→x₃y₃, x₄y₄ входят в подстановку (4) x₂y₂, добавляем к ней

x₃y₃ →F(x₃) = {x₆},P(y₃) ={y₉}→ x₆y₉ входит в подстановку (4)

x₆y₉→F(x₆) = {x₃, x₅,x₇},P(y₉) ={y₃,y₈,y₁₀}→x₃y₃, x₇y₁₀ входят в подстановку (4), x₅y₈ добавляем к ней

x₇y₁₀ →F(x₇) = {x₆, x₈ },P(y₁₀) ={y₇,y₉}→ x₆y₉, x₈y₇ входят в подстановку (4)

x₈y₇ →F(x₈) = {x₄, x₇,x₁₀},P(y₇) ={y₄,y₆,y₁₀}→x₄y₄, x₇y₁₀ входят в подстановку (4), а x₁₀y₆ добавляем к ней

x₄y₄→F(x₄) = {x₁, x₈},P(y₄) ={y₁,y₅}→x₁y₁, x₈y₉ входят в подстановку (4)

x₂y₂→F(x₂) = {x₉, x₁},P(y₂) ={y₁,y₅}→x₁y₁, x₉y₅ входят в подстановку (4)

x₅y₈→F(x₅) = {x₆, x₉},P(y₈) ={y₅,y₉}→x₆y₉, x₉y₅ входят в подстановку (4)

x₁₀y₆ →F(x₁₀) = {x₈, x₉},P(y₆) ={y₅,y₇}→ x₈y₇, x₉y₅ входят в подстановку (4)

окончательно имеем еще одну подстановку

x₁y₁, x₂y₂,x₃y₃, x₄y₄, x₅y₈, x₆y₉, x₇y₁₀, x₈y₇, x₉y₅, x₁₀y₆

Y1

Y2

Y3

Y4

Y8

Y9

Y10

Y7

Y5

Y6

X1

X2

X3

X4

X5

X6

X7

X8

X9

X10

Y1

X1

Y2

X2

Y3

X3

Y4

X4

Y8

X5

Y9

X6

Y10

X7

Y7

X8

Y5

X9

Y6

X10

Графы изоморфны, в чем можно убедиться по идентичности матриц смежности. Аналогичным образом можно получить подстановку и для третьих циклов: окончательно имеем подстановку

x₁y₁, x₂y₂,x₃y₄, x₄y₃, x₅y₆, x₆y₇, x₇y₁₀, x₈y₉, x₉y₅, x₁₀y₈

Это подстановка также сохраняет отношение смежности, следовательно, графы G(X,F) и H(Y,P) изоморфны.

Таким образом, все три подстановки установлены с первого раза, что как минимум иллюстрирует возможность использования дополнительной информации о порядке следования вершин в циклах для распознавания изоморфности.

Результат решения примера показал, во-первых, работоспособность и сходимость алгоритма и, во-вторых, что существует несколько таких подстановок, свидетельствующих о наличии группы автоморфизмов.

Наличие группы автоморфизмов, характеризующих симметрию графов, видно из их графического изображения.

Так, граф G(X,F) можно вращать по и против часовой стрелки относительно неподвижной вершины x₆ на 120^˚ и 240^˚, граф H(Y,P) поворачивать на ±180^˚ относительно неподвижной оси y₁ y₃ y₆ y₉.

Кроме того, можно осуществлять повороты на 120^˚ и 240^˚ вершин циклов x₁ x₂ x₉ x₅ x₆ x₃ x₁; x₁ x₃ x₆ x₇ x₈ x₄ x₁; и x₆ x₇ x₈ x₁₀ x₉ x₅ x₆ и поскольку графы G(X,F) и H(Y,P) изоморфны, то аналогичные автоморфизмы существуют для обоих графов. Понятие автоморфизма нам понадобиться при установлении зависимости между типовыми и конкретными структурами.

Алгоритм работает эффективно при достаточно больших значениях t, когда обнаружено и распознано большинство вершин. При малых значениях t, а следовательно и Pi(t) чаще наблюдаются «осколки» разыгрываемого графа и алгоритм работает неэффективно. Более эффективным в таких условиях является алгоритм, приведённый ниже.

Суть алгоритма заключается в том, что кроме стандартной процедуры сравнения полустепеней исхода и захода конкретной вершины используется информация о характеристиках вершин, смежных с исследуемой для каждого входящего и исходящего ребра, что существенно сокращает число операций при переборе, а следовательно и ускоряет решение всей задачи.

Это объясняется тем, что процедура распознавания изоморфного вложения используется на каждом шаге розыгрыша N* раз.

В блок-схеме алгоритмапринимается, что матрицы A, B и C являются соответственно матрицами смежности эталонного графа, исследуемого графа (меньшей или равной размерности относительно эталонного) и матрицей возможных подстановок. Переменная Mirage «закрывает» ненужные варианты подстановок. Ниже дано краткое описание назначения процедур блок-схемы.

Prioritet - процедура, нахождения строки с наименьшим числом возможных подстановок, присвоения этой строке текущего приоритета, изменение переменной Mirage; (под приоритетом здесь понимается целое число, присваиваемое строке матрицы. Изначально все строки имеют нулевой приоритет. Строка с наибольшим приоритетом является активной, т.е. все корректировки матрицы производятся относительно этой строки).

Prov_0_str - процедура проверки наличия нулевых строк в матрице С, если такие строки есть то Pr_0=1, иначе Pr_0=0, а также заполнение массива C_Kol (Pr_0 -признак “нулевой” строки, C_Kol - копия столбца “количество возможных подстановок”);

Prov_1_str - процедура проверки того, что все элементы массива равны единицам, т.е. выполняется условие, когда графы изоморфны;

Mirage1 - процедура получения координат активной ячейки, “обнуления” активных столбца и строки;

Mirage2 - процедура нахождения строки с единственным элементом ‘1’, после нахождения – обнуление столбца, если последнее производилось то PrMir:=1 (PrMir - признак того, что матрица С корректировалась процедурой Mirage2);

Mirage3 - процедура корректировки таблицы по правилу: Если C[i,j]=’1’ and B[i,FocB]=’1’ and A[i,FocA]¹’1’ то C[i,j]=Mirage

Если C[i,j]=’1’ and B[FocB,j]=’1’ and A[FocA,j]¹’1’ то C[i,j]=Mirage

ExitToHome - процедура возврата (приведения матрицы С к виду, предшествующему последней серии преобразований);

ZapolnMatrCM - процедура заполнения модифицированной матрицы вариантами решения;

ProvEnd - процедура окончательной проверки изоморфного вложения графов.

Далее приведено текстуальное описание работы блок-схемы алгоритма на примере решения задачи нахождения изоморфного вложения.

Матрицы смежности графов А и В, а также матрица возможных подстановок С представлены на рис.5.

Используя метод полного перебора вариантов подстановок для этого примера необходимо проверить 576 вариантов. Разработанный алгоритм позволяет найти решение этой задачи уже на третьем цикле процедуры.

Рис.5 Пример графа-эталона (А) и графа-реализации (В).