Деревья, разрезы, циклы

При исследовании сетей военной связи особое место занимают вопросы связности, ее нарушения и восстановления, синтеза структур с максимальной связностью, зависимости связности от структуры графа, выявление узких мест и условий, необходимых (достаточных) для ее нарушения. Непосредственное отношение к этим вопросам имеют такие понятия теории графов как деревья, разрезы, циклы.

Граф называется ациклическим, если он не содержит циклов. Деревом Т графа G называется ациклический связный подграф графа G. Остовом графа G называют дерево Т графа G, содержащее все вершины графа G. Связный подграф дерева Т называется поддеревом.

Кодерево Т^* остова Т графа G является подграфом графа G, содержащим все вершины графа и только те ребра G, которые не входят в Т.

Ребра остова Т называются ветями Т, а ребра соответствующего кодерева Т^*- хордами.

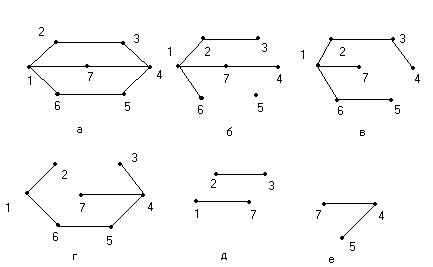
Рис.14. Граф, его деревья, остовы, кодеревья.

а)- граф G; б)-дерево графа G; в,г)- остовные деревья графа G; д,е)-кодеревья к деревьям; г) и в) соответственно.

Нетрудно видеть, что остовное дерево Т содержит n-1 ребер и является минимально связным графом, состоящим из n вершин.

Удаление любого ребра приводит к нарушению связности и образованию 2^х связных компонент дерева.

k- деревом называется ациклический граф, состоящий из k компонент. Если k- дерево является остовным подграфом графа G, то оно называется остовным k-деревом G; k- дерево содержит n-k ребер.

Лесом графа G называется остовное k- дерево графа G, где k- число компонент в G.

Ко- лес Т^* леса Т графа G –это остовный подграф графа G, содержащий те ребра G, которые не входят в Т.

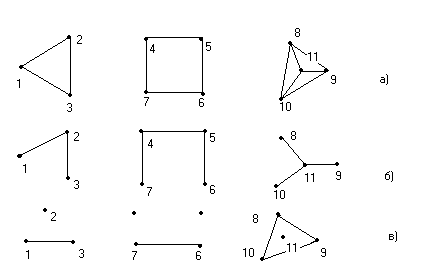
Рис.15. Лес и ко-лес. а)-граф; б)-лес; в)- ко-лес.

Если граф содержит n вершин, m ребер и состоит из k- компонент, то ранг графа, обозначаемый через r(G), определяется выражением: r(G)= n- k, а цикломатическое число, обозначается как m(G) и определяется выражением m(G) = m – n + k. Из выражений для m(G) и r(G) следует, что r(G) + m(G) = m. Рассмотрим граф на рис.15а:

k= 3; n = 11; m = 13, отсюда r(G) = 11-3 = 8; m(G) = 13- 11+3 =5.

Базисным циклом графа G относительно хорды остова Т называется цикл, состоящий из ветвей дерева Т и одной из хорд С_i.

Как отмечалось ранее, множество ветвей дерева Т содержит n-1 ветвь, множество хорд- m-n+1 ребер соответственно и множество всех циклов равно m-n+1. Множество С₁, С₂,…, С_m-n+1 циклов графа G относительно хорд С_i остова Т называется базисным множеством циклов графа G относительно Т.

Отличительной особенностью базисного цикла С_i является то, что он содержит только одну хорду С_i, которая ни в каких других базисных циклах относительно данного остовного дерева Т не встречается.

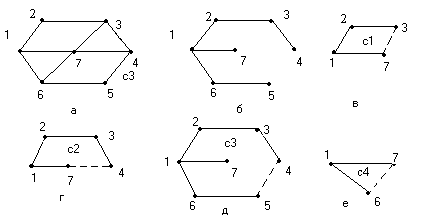
Рис.16. Граф, остов и базисные циклы.

а)- граф G; б)- остов; в;г;д и е)-базисные циклы

Разрезающим множеством графа S называется такое минимальное множество ребер, удаление которых делает граф G-S несвязным. Минимальность понимается в том смысле, что любое подмножество S′Ì S не делает граф G несвязным.

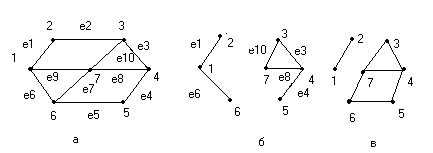
Рис.17. Разрезающие множество графа.

а)- графG; б)- G-S₁; S₁ = {e₂, e₉, e₇, e₅}; в)- G-S₂; S₂= { e₂, e₉, e₇}.

Пусть V = V₁∪ V₂, V₁∩ V₂= Ø, т.е. V₁ и V₂ два непересекающихся множества, а вместе содержат все вершины графа.

Тогда множество S всех таких ребер, которые имеют одну вершину в V₁, а другую в V₂, называется разрезом графа G.

Отличительной особенностью разреза является то, что множество вершин V₁ и V₂ определяются изначально, а сам разрез содержит(является пересечением) несколько реберно- непересекающихся разрезающих множеств.

Если графы, образованные на множествах вершин V₁ и V₂ связные, то разрез S=<V₁,V₂> является минимальным множеством ребер, удаление которых делает граф несвязным и поэтому S=<V₁,V₂> по определению является разрезающим множеством.

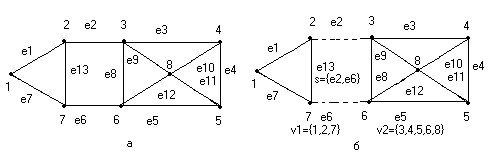
Рис.18. Граф и его разрез.

а)-Граф; б)- V₁={1,2,7}, разрез S={e₂,e₆}, множество V₂={3,4,5,6,8}.

Пусть Т- остов связного графа G, а в_i ветвь Т. При удалении ветви из дерева он разделяется на две компоненты Т₁, Т₂ которые являются деревьями из множеств V₁ и V₂, а V = V₁U V₂, V₁∩ V₂= Ø.

Кроме того Т₁и Т₂являются остовами графов G₁ и G₂, порожденных на множествах вершин V₁ и V₂.

Разрез S= < V₁, V₂> является разрезающим множеством графа G. Это разрезающее множество называется базисным множеством графа G по отношению к ветви в_i остова Т графа G.

Множество всех n-1 базисных разрезающих множеств по отношению к n-1 ветви остова Т связного графа G называется базисным множеством разрезающих множеств графа по отношению к остову Т. Разрезающее множество содержит ровно одну ветвь дерева Т, все остальные его ребра являются хордами.

Для установления взаимосвязи между разрезающими множествами, циклами, деревьями и кодеровьями рассмотрим пример.

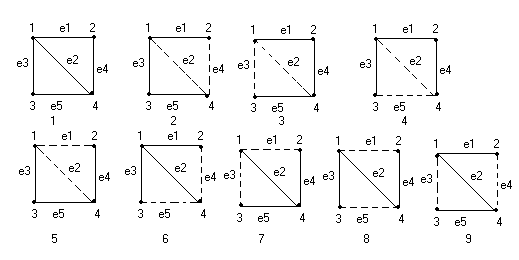
Рис.19. Граф, его остовные деревья и ко-деревья

1-граф G, 2-9-остовные деревья, показаны сплошными линиями, ко-деревья- пунктирными.

Таблица 1.

№		Т1⊏	Т2⊐	Т3⊓	Т4⊔	Т5	Т6	Т7	Т8
	Остовы	е1е3е5	е1е4е5	е1е3е4	е3е4е5	е1е2е3	е2е4е5	е2е3е4	е1е2е5
	Кодеревья	е1е2	е2е3	е2е5	е1е2	е4е5	е1е3	е1е5	е3е4
	Базисные циклы	е1е3е4е5	е1е3е4е5	е1е3е4е5	е1е3е4е5	е1е2е4	е2е3е5	е1е4е4	е2е3е5
	Базисные разрезающие множество	е1е4 е2е3е4 е2е4е5	е1е2е3 е2е3е4 е3е5	е1е2е3 е3е5 е2е4е5	е1е2е3 е1е2е5 е1е4	е1е4 е2е4е5 е3е5	е1е4 е2е3е4 е2е4е5	е1е2е5 е3е5 е1е4	е1е4 е2е3е4 е3е5
	Независимые базисные разрезы	е1е4	е1е2е3	е3е5	е1е2е5	е2е4е5	е2е3е4
	Независимые цикли	е1е3е4е5 для остовов Т1-Т4 и е1е3е4 и е2е4е5 для Т5-Т8