Принципы статистического имитационного моделирования

Для предметного рассмотрения последующих этапов разработки ИМ и, прежде всего, принципов организации алгоритмов модели, необходимо предварительно рассмотреть особенности статистического имитационного моделирования сложных систем.

Важной особенностью процесса функционирования большинства систем во взаимодействии с внешней средой является случайный (вероятностный) характер протекающих в них процессов и явлений. Вероятностные факторы должны быть отражены в модели системы как случайные события, случайные величины (дискретные или непрерывные) или случайные функции (процессы, поля). Если, например, исследуется поведение вычислительной системы, то для всех ее функциональных модулей и схемных элементов вводятся случайные события «отказа», которые должны имитироваться в модели с заданными в качестве исходных данных вероятностями. Подобных, как правило, разнородных факторов случайности в ИМ может быть множество.

В этой ситуации воспроизведение с помощью ИМ одной или нескольких реализаций процесса функционирования системы в течение заданного интервала времени не позволяет сделать обоснованные выводы относительно ее эффективности. Очевидно, также, что наблюдение большого количества подобных реализаций позволяет получить некоторую усредненную картину поведения системы, которая дает возможность судить об интересующих нас свойствах. Подобные исследования изначально связывали с методом статистических испытаний – методом Монте-Карло, появление которого в конце 1940-х гг. определили работы американских ученых в области проектирования средств защиты от ядерных излучений. В классической постановке метод Монте- Карло является численным методом решения аналитических задач и основан на проведении серии однородных в статистическом смысле испытаний для определения вероятностных характеристик случайных величин и случайных функций, отображающих искомые решения. Его применение и развитие в интересах имитационного моделирования сложных систем, функционирующих при наличии различного рода случайных факторов, привело к возникновению метода статистического имитационного моделирования.

В основе метода статистического имитационного моделирования лежит выполнение следующих действий:

- проведение большого количества одинаковых по исходным данным испытаний – актов имитации вероятностного процесса функционирования системы во взаимодействии с внешней средой;

- формирование на этой основе соответствующего количества независимых реализаций случайных величин, характеризующих те или иные исходы функционирования системы в смысле выполнения возлагаемых на нее функций (целей);

- усреднение и иная статистическая обработка формируемых реализаций случайных величин (исходов) с целью получения статистически значимых выводов относительно эффективности системы.

При получении независимых реализаций величин, характеризующих «хорошие» и «плохие» исходы процесса функционирования системы, искомые показатели эффективности (вероятность, точность и т. п.) обычно оцениваются как средние значения по полученным в ходе ИМ экспериментальным данным. Поэтому математические основания метода статистического моделирования, как и метода Монте-Карло, определяются законами больших чисел и предельными теоремами теории вероятностей.

В теории вероятностей доказывается теорема (усиленный закон больших чисел в форме Колмогорова), которая формулируется таким образом: для того чтобы среднее арифметическое независимых реализаций случайной величины U сходилось бы с вероятностью 1 к ее математическому ожиданию, необходимо и достаточно, чтобы это математическое ожидание существовало.

Иначе, пусть – последовательность значений независимых одинаково распределенных величин – реализаций исследуемой случайной величины U, полученных в ходе испытаний модели, причем Пусть также , тогда для любого :

На первый взгляд утверждение теоремы выглядит тривиальным, однако это далеко не так. Оказывается, что далеко не все случайные величины имеют математическое ожидание и дисперсию. Например, для распределения Коши, имеющего плотность и функцию распределения вида:

где h, и ₀ – параметры формы распределения (здесь и ₀ – медиана), математическое ожидание и дисперсия не существуют. Это означает, в частности, что расходится интеграл вида:

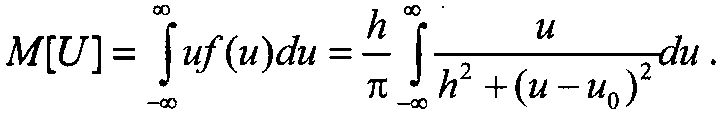
т. е. математическое ожидание данной величины не определено. С точки зрения проведения имитационного эксперимента это означает, что статистическая обработка полученных реализаций U по любому количеству испытаний п в виде оценки среднего S_n / n не гарантирует, что очередное испытание даст оценку S_n+1/ (n + 1), лежащую рядом с ранее полученной оценкой.