 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Общая постановка задачи оптимизации
|
|
Процесс конструирования любого изделия, в том числе ЭВС, всегда включает три основных этапа:
1. Определение требований, которые предъявляются к разрабатываемому устройству, то есть формируется цель, к которой затем стремится конструктор при разработке.
2. Определение существующих ограничений на параметры и характеристики изделия, например по стоимости, элементной базе, потребляемой мощности и т. п.
3. Выбор конкретного варианта конструкции из возможных с учетом сформированной цели и ограничений.
При решении задачи третьего этапа обычно конструктор сталкивается с необходимостью решения определенной задачи оптимизации, которая заключается в выборе (или поиске) наилучшего технического решения по сравнению с другими вариантами по некоторому критерию качества.
1. Будем считать, что любой вариант технического решения определяется некоторым набором числовых параметров, то есть вектором 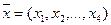 . При этом параметры конструкции не могут быть выбраны произвольно, а принадлежат некоторому числовому множеству
. При этом параметры конструкции не могут быть выбраны произвольно, а принадлежат некоторому числовому множеству 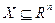 , где
, где 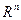 - мерное евклидово пространство.
- мерное евклидово пространство.
2. Множество Х определяется ограничениями на параметры конструкции и называется множеством допустимых решений.
Множество Х в общем случае ограничивается в виде систем уравнений
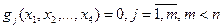 ,
,
либо неравенствами
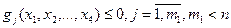
где n- число параметров, m, 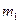 - число ограничений.
- число ограничений.
При этом система уравнений устанавливает количественную связь между параметрами изделия, а система неравенств показывает, что последние могут изменяться в заданных пределах.
3. Каждый вариант решения 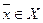 можно охарактеризовать некоторым показателем качества
можно охарактеризовать некоторым показателем качества 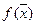 , по которому производится сравнение вариантов. Иначе говоря, на множестве решений
, по которому производится сравнение вариантов. Иначе говоря, на множестве решений 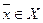 задается некоторая функция
задается некоторая функция 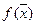 , называемая критерием оптимальности, критерием качества или целевой функцией. Целевая функция количественно показывает степень выполнения требований, предъявляемых к конструкции.
, называемая критерием оптимальности, критерием качества или целевой функцией. Целевая функция количественно показывает степень выполнения требований, предъявляемых к конструкции.
4. С учетом вверенных понятий задача оптимизации формируется следующим образом. Необходимо выбрать конкретный вариант технического решения, описываемый некоторым вектором 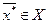 , для которого обеспечивается экстремум целевой функции f(
, для которого обеспечивается экстремум целевой функции f(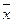 ).
).
Формально требуется найти вектор 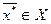 , для которого
, для которого 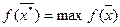 ,
, 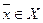 или
или 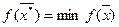 ,
, 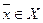 в зависимости от конкретной задачи.
в зависимости от конкретной задачи.
Замечание:
При этом следует учитывать, что целевая функция должна быть скалярной (а не векторной), т. е. оптимизировать можно только по одному критерию качества, а не по нескольким одновременно. Область допустимых решений Х задается системой уравнений или неравенств указанного вида.
Замечание 2:
Задачу максимизации функции f(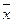 ) всегда можно заменить минимизацией функции
) всегда можно заменить минимизацией функции 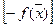 .
.
Дата публикования: 2015-09-18; Прочитано: 879 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
