Примеры решения типовых задач. Пример 1. Провести полное исследование функции

Пример 1. Провести полное исследование функции

Решение.

1) .

2) , т.е. и . Функция является функцией общего вида, непериодической.

3) Так как , то график пересекает оси координат только в точке .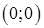

4) .

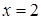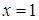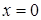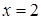или . не существует в точке , но она не входит в область определения функции. Следовательно, имеются две стационарные точки и . Разобьем этими точками область определения на интервалы знакопостоянства производной: 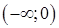, , 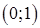, 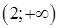. Определим знаки производной в этих интервалах (см. рис. 15).

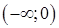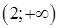Используя достаточные условия монотонности и экстремума, можно сделать следующие выводы: функция возрастает в интервалах и , убывает в 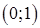и . Значение максимума , значение минимума .

5) .

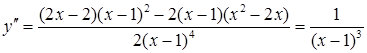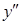не обращается в 0, а в точке 1, где 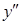не существует, функция не определена, поэтому график функции не имеет точки перегиба. Таким образом, имеются два интервала и , знакопостоянства второй производной (см. рис.16).

В силу достаточных условий выпуклости и вогнутости графика в интервале график выпуклый (вверх), а в интервале график вогнутый (выпуклый вниз).

6)Так как , , 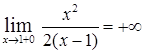то прямая 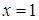– вертикальная асимптота графика функции.

.

.

Следовательно, прямая – наклонная асимптота графика функции при .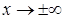

7) Построим график функции. Сначала изобразим асимптоты 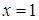и (пунктирной линией). Наносим на чертеж точки (0, 0) и (2, 2), найденные в пункте 4. Проводим через эти точки линию, согласно результатам исследования функции в пунктах 4, 5, 6. Еще раз сравниваем полученный график с результатами исследования и убеждаемся в правильности построения графика.

Пример 2. Провести полное исследование функции .

Решение.

1)

2) , т.е. и . Функция является функцией общего вида, непериодической.

3) Так как в точке x = 0 функция не определена и

, ,

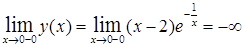то график функции “подходит” справа к началу координат.

Чтобы найти точки пересечения графика функции с осью 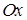, решим уравнение Значит, график пересекает ось 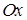при 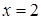. Обозначим эту точку .

4)

Производная не существует в точке 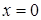, но в ней функция не определена, поэтому она не является критической. Таким образом, стационарными являются точки 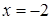и

Разобьем стационарными точками область определения на интервалы и нейдем в них знаки производной (см. рис.18).

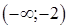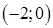Таким образом, функция возрастает в интервалах и , убывает в интервалах и 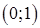, 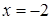– точка максимума, максимальное значение равно , 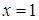– точка минимума, минимальное значение равно .

5)

Вторая производная существует во всех точках области определения функции, значит, точка перегиба может быть только при таких значениях 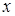, что 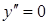. Решив уравнение , получим . Эта точка разбивает область определения функции на интервалы, в каждом из которых 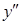сохраняет знак (см. рис.19).

Таким образом, функция выпукла (вверх) в интервалах 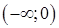и , вогнута (выпукла вниз) в интервале , является абсциссой точки перегиба, , – точка перегиба графика функции.

6) Вертикальная асимптота может быть в точке разрыва 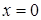. Найдем односторонние пределы функции в этой точке.

,

Следовательно, прямая 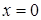является вертикальной асимптотой при слева.

,

, т.к. по правилу Лопиталя

,

.

Таким образом, прямая является наклонной асимптотой.

7) Строим график функции (рис.20).

Задания для самостоятельной работы

n 73. Провести полное исследование функций.

а) ;	б)
в)	г)
д)	е)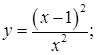
ж)	з)
и)	к) .

n 74. Провести полное исследование функций.