 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Промежутки монотонности и экстремумы функций
|
|
Определение. Функция 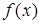 называется возрастающей (убывающей) в промежутке
называется возрастающей (убывающей) в промежутке 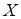 из области определения, если для любых
из области определения, если для любых  из условия
из условия  следует неравенство
следует неравенство  (соответственно
(соответственно 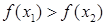 ).
).
На рисунке 8 а) функция возрастает в интервалах 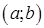 ,
,  , убывает в
, убывает в  .
.
Под монотонностью понимается либо возрастание, либо убывание.
Теорема 3 (достаточное условие монотонности). Если функция 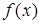 дифференцируема в промежутке
дифференцируема в промежутке 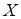 и
и  (
( ) для всех
) для всех 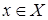 , то
, то 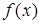 возрастает (соответственно убывает) в промежутке
возрастает (соответственно убывает) в промежутке 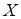 .
.
Определение. Точка  называется точкой минимума (максимума) функции
называется точкой минимума (максимума) функции 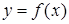 , если она определена в некоторой окрестности этой точки и для каждой точки
, если она определена в некоторой окрестности этой точки и для каждой точки  этой окрестности
этой окрестности  (соответственно
(соответственно  ). Значение функции
). Значение функции  называется минимумом (соответственно максимумом).
называется минимумом (соответственно максимумом).
На рис. 8 а)  – точка максимума,
– точка максимума, 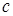 – точка минимума.
– точка минимума.
Под экстремумом функции (локальным) понимается либо минимум функции, либо её максимум.
Определение Точка  из области определения функции
из области определения функции 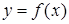 , называется стационарной точкой, если
, называется стационарной точкой, если 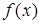 дифференцируема в
дифференцируема в  и
и 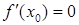 .
.
Определение Точка  из области определения функции
из области определения функции 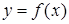 , называется критической точкой, если
, называется критической точкой, если 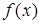 не дифференцируема в
не дифференцируема в  .
.
На рис.8 б)  – критическая, а на рис. 8 в) точка
– критическая, а на рис. 8 в) точка  – стационарная.
– стационарная.

Необходимое условие экстремума. Если  - точка экстремума функции
- точка экстремума функции 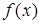 , то она является стационарной ил критической точкой этой функции.
, то она является стационарной ил критической точкой этой функции.
На рис. 8 б) критическая точка  является точкой экстремума, а на рис. в стационарная точка
является точкой экстремума, а на рис. в стационарная точка  не является точкой экстремума. Таким образом, не всякая критическая или стационарная точка является точкой экстремума.
не является точкой экстремума. Таким образом, не всякая критическая или стационарная точка является точкой экстремума.
Первое достаточное условие экстремума. 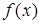 непрерывна в точке
непрерывна в точке  и дифференцируема в
и дифференцируема в  Пусть
Пусть  - стационарная или критическая точка функции
- стационарная или критическая точка функции 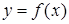 . Если в некоторой окрестности точки
. Если в некоторой окрестности точки  слева от
слева от  производная
производная 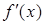 принимает один знак, а справа от
принимает один знак, а справа от  - противоположный, то
- противоположный, то  - точка экстремума. При этом если слева
- точка экстремума. При этом если слева  , справа
, справа  , то
, то  - точка максимума, в противном случае
- точка максимума, в противном случае  - точка минимума. Если в некоторой проколотой окрестности точки
- точка минимума. Если в некоторой проколотой окрестности точки  производная
производная 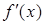 имеет постоянный знак, то
имеет постоянный знак, то  не является точкой экстремума. Если к тому же
не является точкой экстремума. Если к тому же 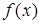 непрерывна в
непрерывна в  , то функция монотонна в этой окрестности (рис. 8 в)).
, то функция монотонна в этой окрестности (рис. 8 в)).
Второе достаточное условие экстремума. Пусть 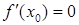 и существует
и существует 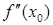 . Тогда если
. Тогда если  , то
, то  - точка минимума. Если же
- точка минимума. Если же 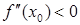 , то
, то  - точка максимума.
- точка максимума.
Вторым достаточным условием экстремума удобно пользоваться, если достаточно сложно установить знак первой производной в окрестности точки экстремума.
Дата публикования: 2015-09-17; Прочитано: 737 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
