 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства линейной зависимости
|
|
Свойство 1. Система из одного вектора  линейно зависима тогда и только тогда, когда
линейно зависима тогда и только тогда, когда  .
.
Свойство 2. Система, содержащая более одного вектора, линейно зависима тогда и только тогда, когда среди векторов есть такой, который является линейной комбинацией остальных векторов.
Свойство 3. Если часть системы линейно зависима, то и вся система линейно зависима.
Следствие 4.1. Система, содержащая нулевой вектор, линейно зависима.
Утверждение 4.1. Если система  линейно независима, но при добавлении к ней еще одного ненулевого вектора
линейно независима, но при добавлении к ней еще одного ненулевого вектора  становиться линейно зависимой, то вектор
становиться линейно зависимой, то вектор  линейно выражается через
линейно выражается через  .
.
Определение 4.11. Система векторов  называется максимальной линейно независимой системой векторов, если при добавлении к ней еще одного ненулевого вектора она становится линейно зависимой.
называется максимальной линейно независимой системой векторов, если при добавлении к ней еще одного ненулевого вектора она становится линейно зависимой.
4.8. Найти линейную комбинацию  векторов:
векторов:
1.  ;
;  ;
; 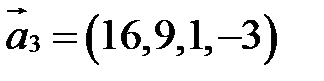 ;
;
2.  ;
; 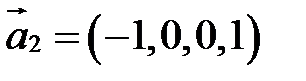 ;
;  .
.
4.9. Выяснить, являются ли следующие системы векторов линейно зависимыми:
1.  ,
,  ; 2.
; 2.  ,
, 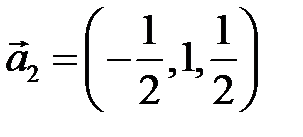 ; 3.
; 3.  ,
,  ,
,  ; 4.
; 4.  ,
,  ,
,  ;
;
5.  ,
,  ,
,  ,
,  ;
;
6.  ,
,  ,
,  ,
,  .
.
4.10. Доказать, что система векторов, содержащая два равных вектора, линейно зависима.
4.11. Доказать, что система векторов, содержащая нулевой вектор, линейно зависима.
4.12. Доказать, что если часть системы векторов, линейно зависима, то и вся система линейно зависима.
Дата публикования: 2015-09-17; Прочитано: 356 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
