 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Контрольная работа №2. 71-80.Вычислить площадь фигуры, ограниченной параболой
|
|
71-80. Вычислить площадь фигуры, ограниченной параболой
y = ax2 + bx + c и прямой y = kx + 1. Сделать чертеж.
| 71. | y = -x2 + 4 x – 1; | y = -x – 1. |
| 72. | y = x2 - 6 x + 7; | y = x + 1. |
| 73. | y = -x2 + 6 x + 7; | y = x + 1. |
| 74. | y = -x2 + 4 x – 1; | y = x - 5. |
| 75. | y = -x2 + 6 x – 5; | y = -x + 1. |
| 76. | y = x2 + 6 x + 7; | y = x + 7. |
| 77. | y = -x2 - 6 x – 5; | y =- x + 1. |
| 78. | y = x2 + 6 x + 7; | y = -x + 1. |
| 79. | y = -x2 - 6 x – 5; | y = -x – 5. |
| 80. | y = x2 - 4 x + 1; | y = x + 1. |
81-90. Найти неопределенные интегралы. Результаты проверить дифференцированием.
81. а) 
| б) 
|
82. а) 
| б) 
|
83. а) 
| б) 
|
84. а) 
| б) 
|
85. а) 
| б) 
|
86. а) 
| б) 
|
87. а) 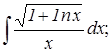
| б) 
|
88. а) 
| б) 
|
89. а) 
| б) 
|
90. а) 
| б) 
|
91-100. Вычислить по формуле Ньютона-Лейбница определенный интеграл 
91. 
| 92. 
| 93. 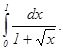
| 94. 
|
95. 
| 96. 
| 97. 
| 98.  
|
99. 
| 100. 
|
101-110. Решить дифференциальное уравнение:
101. 
| 102. 
|
103. 
| 104. 
|
105. 
| 106. 
|
107. 
| 108. 
|
109.. 
| 110. 
|
111-120. Найти частные решения уравнения, удовлетворяющие заданным начальным условиям:
| 111. |  если у = -1, если у = -1,  при х = 0. при х = 0.
|
| 112. |  если у = 1, если у = 1,  = 1 при х = 0. = 1 при х = 0.
|
| 113. |  если у = - 3, если у = - 3, 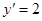 при х = 0. при х = 0.
|
| 114. |  если если 
|
| 115. |  если у (0) = 1, если у (0) = 1, 
|
| 116. |  если у (0) = 2, если у (0) = 2, 
|
| 117. | 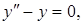 если у (0) = 0, если у (0) = 0, 
|
118.  если у (0) = 1,
если у (0) = 1, 
119.  если у (0) = 1,
если у (0) = 1, 
120.  если у = 1 и
если у = 1 и  при х = 0.
при х = 0.
121-130. Найти частные производные второго порядка следующих функций:
121.  126.
126. 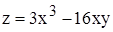
122.  127.
127. 
123.  128.
128. 
124.  129.
129. 
125.  130.
130.  .
.
131-140. С помощью двойного интеграла найти площадь фигуры, ограниченной параболой и прямой.
| 131. | y = x2 - 4x + 3 | y = -x + 1 |
| 132. | y = -x2 +2x + 2 | y = -x -2 |
| 133. | y = x2 - 3 | y = x - 1 |
| 134. | y = -x2 - 6x + 5 | y = -x - 1 |
| 135. | y = x2 - 3x + 1 | y = x - 2 |
| 136. | y = -x2 - 2x | y = x + 2 |
| 137. | y = x2 -3x | y = -x + 3 |
| 138. | y = -x2 - 2x - 1 | y = -x - 3 |
| 139. | y = x2 + 5x +6 | y = x + 3 |
| 140. | y = -x2 + 6x + 3 | y = x - 3 |
141-150. Вычислить приближенные значения определенных интегралов с помощью разложения подынтегральной функции в ряд (использовать три первых члена ряда).
141. 
| 142. 
|
143. 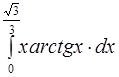
| 144. 
|
145. 
| 146. 
|
147. 
| 148. 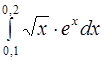
|
149. 
| 150. 
|
151-160. Определить радиус сходимости и область сходимости степенных рядов с общим членом ряда:
151. 
| 152. 
| |
153. 
| 154. 
| |
155. 
| 156. 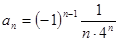
| |
157. 
| 158. 
| |
159. 
| 160. 
| |
Вопросы к экзамену
Дата публикования: 2015-09-17; Прочитано: 1091 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
