Задания для контрольных работ

Контрольная работа №1

1-10. Даны вершины А (х₁; у₁), В (х₂; у₂), С (х₃; у₃) треугольника. Найти:

- длину стороны АВ;

- уравнение высоты, проведенной через вершину С;

- уравнение медианы, проведенной через вершину С.

1.	А (3; 1),	В (7; -4)	С (4; 5)
2.	А (2; 1),	В (-5; 4)	С (-2; 1)
3.	А (-3; 1),	В (5; 4)	С (0; 5)
4.	А (-1; 0),	В (-7; 4)	С (-4; 5)
5.	А (0; -1),	В (7; 2)	С (4; 5)
6.	А (1; -1),	В (-5; 2)	С (-2; 3)
7.	А (-1; -1),	В (5; 2)	С (2; 3)
8.	А (-1; -1),	В (-7; 2)	С (-4; 3)
9.	А (4; 1),	В (6; 4)	С (3; 5)
10.	А (1; 0),	В (5; 3)	С (4; 4)

11-20.

11.Составьте уравнение эллипса, фокусы которого лежат на оси ординат, ε = 0,6 и 2 b = 10.

12. Составьте уравнение эллипса, фокусы которого имеют координаты (; 0) и (; 0), а большая ось равна

13. Составьте уравнение гиперболы, если расстояние между фокусами 2 с = 10, уравнения асимптот имеют вид у = ± 0,5 х.

14. Составьте уравнение асимптот гиперболы 4 х² – 9 у² = 36 и найдите координаты ее фокусов и эксцентриситет.

15. Составьте уравнение эллипса, проходящего через точки А () и В (), если его фокусы лежат на оси абсцисс.

16. Составьте уравнение эллипса, координаты фокусов которого (-7; 0) и (7; 0), а эксцентриситет ε = 0,28.

17. Составьте простейшее уравнение гиперболы 9 х² – 16 у² = 11.

18. Эллипс задан уравнением Найти координаты фокусов эллипса, фокусное расстояние и эксцентриситет.

19. Найдите эксцентриситет гиперболы 25 х² – 49 у² = 1225.

20. Найдите координаты фокусов, длины осей и эксцентриситет эллипса, заданного уравнением 16 х² + 25 у² = 400.

21-30. Найти матрицу, обратную матрице.

Проверить результат, вычислив произведение данной и полученной матриц.

21.	22.	23.
24.	25.	26.
27.	28.	29.
30.

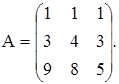
31-40. Решите системы уравнений тремя способами: по формулам Крамера, методом Гаусса, при помощи обратной матрицы:

31.	32.	33.
34.	35.	36.
37.	38.	39.
40.

41-50. Найти пределы функций.

41. 1) при а) х₀ = 2, б) х₀ = 3, в) х₀ = ∞;

2)

42. 1) при а) х₀ = 0, б) х₀ = 2, в) х₀ = ∞;

2)

43. 1) при а) х₀ = -3, б) х₀ = -2, в) х₀ = ∞;

2)

44. 1) при а) х₀ = 3, б) х₀ = -3, в) х₀ = ∞;

2)

45. 1) при а) х₀ = 2, б) х₀ = 4, в) х₀ = ∞;

2)

46. 1) при а) х₀ = 2, б) х₀ = 5, в) х₀ = ∞;

2)

47. 1) при а) х₀ = 1, б) х₀ = -4, в) х₀ = ∞;

2)

48. 1) при а) х₀ = 5, б) х₀ = -5, в) х₀ = ∞;

2)

49. 1) при а) х₀ = -2, б) х₀ = -1, в) х₀ = ∞;

2)

50. 1) при а) х₀ = -2, б) х₀ = 1, в) х₀ = ∞;

2)

51-60. Найти производные заданных функций.

51. а)

б)

52. а)

б)

53. а)

б)

54. а)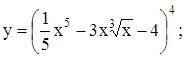

б)

55. а)

б)

56. а)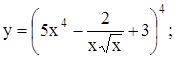

б)

57. а)

б)

58. а)

б)

59. а)

б)

60. а)

б)

61-70. Исследовать средствами дифференциального исчисления функцию у = ƒ(х) и построить ее график.

61. ƒ(х) =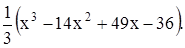

62. ƒ(х) =

63. ƒ(х) =

64. ƒ(х) =

65. ƒ(х) =

66. ƒ(х) =

67. ƒ(х) =

68. ƒ(х) =

69. ƒ(х) =

70. ƒ(х) =