Высшего профессионального образования 5 страница

1 способ. Решим эту задачу по общим правилам, не прибегая к методам преобразования комплексного чертежа (рис. 8.9)

Алгоритм решения заключается в следующем

1. Через точку М проводим прямую n, перпендикулярную плоскости (АВС) (h – горизонталь, f – фронталь этой плоскости, n₁┴h₁, n₂┴f₂).

2. Найдем точку N пересечения прямой n с плоскостью (АВС) (∑ € n, ∑ ┴ П₂, ∑ П (АВС) = (12), (12) П n =N).

3. Построим отрезок N₂N^” равный искомой величине /MN/. На рис. 8.9 это сделано способом прямоугольного треугольника.

2 способ. Применим метод замены плоскостей проекций (рис. 8.10).

1. Дополнительную плоскость проекций П₄ следует выбирать перпендикулярно плоскости (АВС). Условия метода требуют, чтобы П₄ была перпендикулярна одной из плоскостей проекций, например П₁. Тогда П₄ необходимо провести перпендикулярно горизонтали плоскости h, т.е. х₁₄ ┴ h₁.

2. Построим проекции данной плоскости и точки М на П₄. Очевидно, что на П₄ плоскость (АВС) проецируется в прямую А₄В₄.

3. M₄N₄ ┴ А₄В₄. / M₄N₄/ - искомая величина.

3 способ. Применим метод вращения вокруг проецирующей оси.

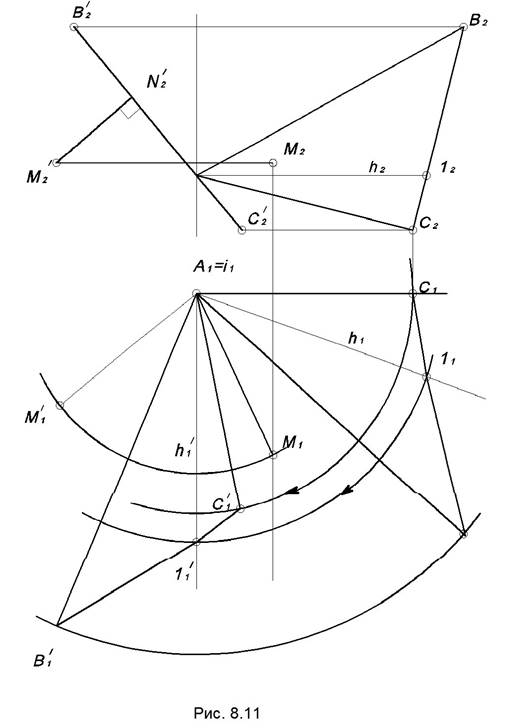
1. Проведем ось вращения i через одну из вершин треугольника АВС, например через А, i ┴ П₁. Через эту же вершину следует провести горизонталь плоскости h (рис. 9.11).

2. Повернем горизонталь h вокруг i так, чтобы она стала фронтально проецирующей прямой h^’.

3. На тот же угол и вокруг той же оси следует повернуть все вершины треугольника АВС и точку М. После поворота плоскость (АВС) на фронтальную плоскость проекций проецируется в прямую В₂^’C₂^’, а отрезок MN, равный расстоянию от точки М до плоскости (АВС) в натуральную величину.

Задача. Построить натуральную величину треугольника АВС.

Эту задачу можно решить многими способами. Рассмотрим два из них.

1 способ. С применением метода замены плоскостей проекций (рис. 8.11).

В данном случае плоскость (АВС) является плоскостью общего положения, значит и плоскость ей параллельная не может быть перпендикулярна ни к П₁, ни к П₂. Поэтому метод замены здесь следует применять дважды.

1. Выберем П₄┴ П₁ и П₄ ┴(АВС), следовательно х_{14 ┴} h₁, где h – горизонталь (АВС). Тогда проекция А₄В₄С₄ – отрезок прямой.

2. Плоскость П₅ должна быть параллельна плоскости (АВС), т.е. х₄₅ ║ А₄С₄, и А₅В₅С₅ есть натуральная величина данного треугольника. Это дает возможность измерить стороны, углы, площадь и другие элементы треугольника АВС.

2 способ. Вращение вокруг линии уровня (рис. 8.13).

Проведем горизонталь h треугольника АВС, h € А. Повернем треугольник вокруг горизонтали h так, чтобы его плоскость стала горизонтальной, тогда на П₁ треугольник спроецируется в натуральную величину. Траектория движения вершины В – окружность К, плоскость которой перпендикулярна оси вращения h. Следовательно, горизонтальная проекция этой окружности – отрезок прямой k₁. k₁ ┴ h₁. k₁ П h₁ = О₁. О – центр окружности к. ОВ – радиус вращения точки В. После поворота радиус вращения ОВ спроецируется в натуральную величину. Поэтому следует определить натуральную величину r отрезка ОВ. (на рис. 8.13это выполнено методом прямоугольного треугольника). /О₁В₁^’/ = r.

Чтобы найти положение вершины С после поворота достаточно построить проекцию траектории m движения точки С и найти точку ее пересечения с прямой В₁^’l₁. (точка А и 1 не меняют своего положения, т.к. принадлежат оси вращения). А₁В₁^’C₁^’ натуральная величина треугольника АВС.

Задача. Определить расстояние от точки М до прямой l.

Классический способ решения (рис. 8.14) этой задачи описывается следующим алгоритмом.

1. Через данную точку М проведем плоскость О (h*f), перпендикулярную l/

2. Найдем точку N пересечения этой плоскости с прямой l.

3. Определим натуральную величину отрезка MN/

Эту же задачу можно решить, применяя дважды метод замены плоскостей проекций (рис. 8.15).

Плоскость П₄ выбираем параллельно прямой l, а П₅ перпендикулярно ей. Тогда на плоскость П₅ данная прямая спроецируется в точку, а отрезок, намеряющий искомое расстояние, - в натуральную величину.

Аналогично можно решать задачи на определение расстояния между двумя прямыми или величины двугранного угла.

8.3 Нормаль поверхности

Нормалью поверхности в точке М называется прямая, проходящая через М и перпендикулярная касательной плоскости в этой точке.

Построение касательной плоскости к сфере рассмотрено в главе 4. Аналогично можно построить касательную плоскость к любой поверхности. Проанализируем возможные способы построения нормали тора Ф в некоторой точке М.

Для построения касательной плоскости через точку М следует провести две линии, принадлежащие поверхности (рис 8.16), например параллель p и меридиан m, и построить касательные к ним b и h в точке М. Тогда касательная плоскость О задана пересекающимися прямыми b и h, причем h – горизонталь. Построим фронталь f, f € О. Искомая нормаль n проходит через М и перпендикулярна О (n₁┴h₁, n₂┴f₂).

В общем случае это решение является приближенным, т.к. приближенно строится линия b и касательная к ней.

Более точное решение можно получить, применяя методы преобразования комплексного чертежа.

На рис. 8.17 эта задача решена методом вращения. Данная поверхность повернута вокруг оси вращения так, чтобы меридиан m занял положение главного меридиана m^’. М₂^’ € m₂^’. Тогда касательная плоскость О спроецируется в прямую О₂^’, n^’ (n₁^’,n₂^’) – нормаль поверхности в точке М^’, b^’ € O^’, b^’ – фронталь плоскости O^’, n₂^’ ┴ b₂^’, b^’ П i = А; n^’ П i = В. Точки А и В неподвижны, т.к. принадлежат оси вращения. При обратном вращении плоскость О^’ займет положение О (h*b), b = АМ, и нормаль n совпадает с прямой ВМ.

Эту же задачу можно решить методом замены плоскостей проекций, для этого дополнительную плоскость следует выбирать параллельно плоскости меридиана, проходящего через данную точку.

9. Развертки поверхностей

В промышленности применяется большое количество разнообразных конструкций, выполненных из листового материала путем изгибания, например наружная обшивка фюзеляжа самолета, вентиляционные каналы, различного рода резервуары. Один из этапов проектирования таких листовых конструкций является построение разверток.

Представим поверхность в виде гибкой, но не растяжимой пленки. Оказывается, при таком условии некоторые поверхностей можно, постепенно изгибать, совмещать с плоскостью так, что при этом не возникает ни разрывов, ни складок. Поверхности, обладающие указанным свойством (многограммые, конические, цилиндрические, торсовые), называют развертывающимися, а фигуру, полученную от совмещения поверхности с плоскостью – разверткой. Все остальные виды поверхностей относятся к неразвертывающимся.

Если рассматривать поверхность Ф и ее развертку Ф₀ как точечные множества, то при условии совмещения поверхности с плоскостью между этими двумя множествами устанавливается взаимно однозначное непрерывное соответствие: каждой точке А поверхности Ф соответствует единственная точка А₀ на развертке Ф₀, каждой линии АВ на поверхности Ф соответствует определенная линия А₀В₀ на развертке Ф_0, и наоборот.

Полученные т.о. развертки обладают следующими свойствами:

· Длины двух соответственных отрезков линий развертки и поверхности равны между собой.

· Углы, образованные линиями на поверхности, и углы между соответствующими линиями на развертке также равны.

· Замкнутая линия на поверхности, и соответствующая ей линия на развертке ограничивают фигуры, площади которых равны между собой.

Следовательно, площадь развертки равна площади самой поверхности.

Преобразования, обладающие свойством сохранения углов, называются конформными преобразованиями, поэтому можно сказать, что поверхность и ее развертка конформны.

Прямая на поверхности переходит в прямую на развертке.

Причем параллельным прямым поверхности соответствует параллельные прямые на развертке. Это утверждение справедливо только при переходе от поверхности к развертке, но не наоборот.

Линия на поверхности, которым на развертке соответствуют прямые, называются геодезическими линиями. По геодезическим линиям определяют кротчайшее расстояние между точками на поверхности.

9.1 Построение разверток многогранных поверхностей

Для получения развертки многогранной поверхности необходимо разрезать ее по некоторым ребрам и последовательно совместить все ее грани с одной плоскостью так, чтобы образовалась связная фигура.

Для одной и той же фигуры вид поверхности развертки может быть различным в зависимости от избранной последовательности в расположении граней на развертке.

Все грани на развертке изображаются в натуральную величину, поэтому построение развертки сводится к определению натуральных величин отдельных граней поверхности.

В качестве примера рассмотрим построение полной развертки поверхности трехгранной пирамиды SАВС (рис. 9.1).

Вначале построим основание пирамиды, натуральную величину А_{1 1 1} которого определим методом вращения вокруг проецируемой прямой i. Величину боковых ребер SA, SB и SC можно определить вращением вокруг проецируемой прямой j. Отрезки S₂А₂^’, S₂В₂^’ и S₂С₂^’ равны длинам соответствующих боковых ребер заданной пирамиды.

Построение развертки можно провести в следующем порядке.

1. Построить ∆ А₀В₀С₀ = ∆ А_{1 1 1.}

2. На каждом из ребер основания построить боковые грани, использую найденные натуральные величины боковых ребер S₂А₂^’, S₂В₂^’ и S₂С₂^’ пирамиды.

Полученная плоская фигура является разверткой поверхности данной пирамиды.

Развертку боковой поверхности призмы, заданной на рис. 9.2 выполним способом нормального сечения.

По условию боковые ребра призмы параллельны плоскости П₂. Пересечем призму плоскостью ∑, перпендикулярной ее боковым ребрам. Сечение призмы такой плоскостью называется нормальным. Натуральный вид нормального сечения M₄N₄F₄ на рис. 9.2 найден с помощью замены плоскостей П₁ на П₄.

Зная величины сторон нормального сечения к длины боковых ребер, можно определить натуральный вид каждой грани и построить развертку.

Если разрезать призму по одному из боковых ребер и развернуть боковую поверхность, то стороны нормального сечения окажутся на прямой, перпендикулярной боковым ребрам.

Порядок построения развертки боковой поверхности призмы.

1. Определим натуральный вид M₄N₄F₄ нормального сечения MNF.

2. На прямой а₀ откладываем отрезки M₀N₀, N₀F₀, F₀M₀, равные сторонам нормального сечения M₄N₄, N₄F₄, F₄M₄,(спрямляем нормальное сечение).

3. Через точки M₀, N₀, F₀, M₀ проводим прямые, перпендикулярные прямой а₀, и откладываем на них отрезки, равные отрезкам боковых ребер призмы, с учетом их расположения по отношению к плоскости ∑ (выше или ниже). Ф₀ – развертка боковой поверхности призмы.

9.2 Построение приближенных разверток развертывающихся поверхностей

Теоретически можно получить точную развертку развертывающейся поверхности, по но практически это выполнить невозможно и нет необходимости. Поэтому при построении разверток поверхностей удобно использовать графические приемы. Криволинейные поверхности аппроксимируют (приближенно замечают) поверхностями вписанных или описанных многогранников, грани которых треугольники или четырехугольники; строят развертки этих многогранников и выполняют обводы концевых точек ребер развернутой поверхности.

При графическом выполнении развертки всегда приходится проводить спрямление или разгибание кривых линий, принадлежащих поверхности. С этой целью применяется способ малых хорд. Как показывает название способа, он заключается в том, что в спрямляемую или разгибаемую кривую (плоскую или пространственную) вписывается ломанная линия, звенья которой представляют небольшие хорды рассматриваемой кривой. Если кривую нужно спрямить, то ее хорды последовательно откладываются на некоторой прямой и полученный отрезок принимаются за приближенную длину дуги кривой.

Аппроксимируя заданную развертывающуюся поверхность поверхностью вписанного или описанного многогранника, получаем в большинстве случаев треугольные или четырехугольные грани. В том случае, когда аппроксимирующая многогранная поверхность имеет треугольные грани, способ построения развертки называют способом триангуляции.

В качестве примера применения способа триангуляции рассмотрим построение развертки конической поверхности, заданной направляющей а и вершиной S (рис. 9.3).

Аппроксимируем коническую поверхность поверхностью незамкнутой пирамиды, вписанную в заданную поверхность. За основание пирамиды примем ломанную, вписанную в направляющую а. Длина отрезков ломанной линии выбирается в зависимости от требуемой точности получения развертки: отрезки ломанной выбираются тем меньше, чем выше требование точности получаемой развертки.

Построим развертку этой пирамиды. Ребра ее основания в данном случае на плоскость П₁ проецируется в натуральную величину. Для определения истинных величин боковых ребер вписанного многогранника используем способ вращения. Если в качестве направляющей выступает некоторая пространственная кривая, или плоскость плоской кривой занимает общее положение, то необходимо еще дополнительно определить натуральные величины отрезков, составляющих ломанную, вписанную в направляющую.

Порядок построения приближенной развертки конической поверхности:

1. На произвольной прямой l от произвольной ее точки, принятой за S откладываем отрезок А₀S₀, / А₀S₀/ = /А₂^’S₂/.

2. На А₀S₀ достраиваем треугольник А₀S₀1₀ со сторонами А₀1₀ и S₀1₀, / А₀1₀/ = / А₁1₁/, / S₀1₀/ = / S₂1₂^’/.

3. Последовательно строим на развертке треугольники 1₀S₀2₀, 2₀S₀3₀ и т.д., соответственно конгруэнтные граням аппроксимирующего многогранника.

4. Ломанную линию А₀1₀ 2₀3₀ В₀ заменяем лекальной кривой, проходящей через вершины ломанной. Полученная на рис. 9.3 фигура Ф₀ является приближенной разверткой заданной конической поверхности.

При построении приближенной развертки цилиндрической поверхности в качестве аппроксимирующей используется поверхность призмы. Рассмотрим построение приближенной развертки цилиндрической поверхности способом нормального сечения.

На рис. 9.4 показан пример построения цилиндрической поверхности.

Предварительно в заданную поверхность следует вписать призму, боковые ребра которой совпадают с некоторыми образующими цилиндрической поверхности. Дальнейшее построение развертки аналогично построению развертки призмы (см. рис. 9.2).

Порядок построения развертки следующий:

1. Рассечем цилиндр плоскостью ∑, перпендикулярной образующим.

2. Натуральный вид нормального сечения определим с помощью замены плоскости П₁ на П₄ ║∑.

3. Спрямим кривую нормального сечения, последовательно отложив длины хорд нормального сечения /M₂N₂/ = /M₄N₄/, /N₂K₂/ = /N₄K₄/, /К₂F₂/ = /K₄F₄/ на произвольной прямой а₂.

4. Через точки M₂ N₂ К₂ F₂ проведем прямые, перпендикулярные а₂, отложим на них отрезки, равные отрезкам соответствующих образующих (ребер призмы) и выполним обводы концевых точек образующих.

Полученная плоская фигура является приближенной разверткой рассматриваемого цилиндра.

Следует отметить, что если образующие цилиндрической поверхности не параллельны плоскости проекций, то целесообразно преобразовать комплексный чертеж так, чтобы образующие данной поверхности заняли положение прямого уровня.

9.3 Построение условных разверток неразвертывающихся поверхностей

В технике довольно часто приходится встречаться с задачей построения разверток таких поверхностей, которые относятся к числу неразвертывающихся. Примером могут служить поверхности больших сферических резервуаров, выполняемых из листовой стали, кровельные перекрытия, отдельные тонкостенные оболочки. Теоретически у неразвертывающихся поверхностей разверток быть не может. Однако на практике приходится прибегать к построению так называемых разверток указанных поверхностей, которые принято называть условными.

Для построения условных разверток заданную поверхность приближенно заменяют (аппроксимируют) некоторой совокупностью развертывающихся поверхностей, развертки которых и принимают за условную развертку данной неразвертывающейся поверхности. Условная развертка неразвертывающейся поверхности принципиально отличается от приближенной развертки развертывающейся поверхности. При построении приближенной развертки ее можно практически с любой степенью точности приблизить к заданной поверхности, увеличивая число граней заменяющего многогранника. Для условной развертки это принципиально не может быть осуществлено, т.к. сколько бы мы не увеличивали степень приближения, получим в итоге не развертку исследуемой поверхности, а развертки заменяющих поверхностей.

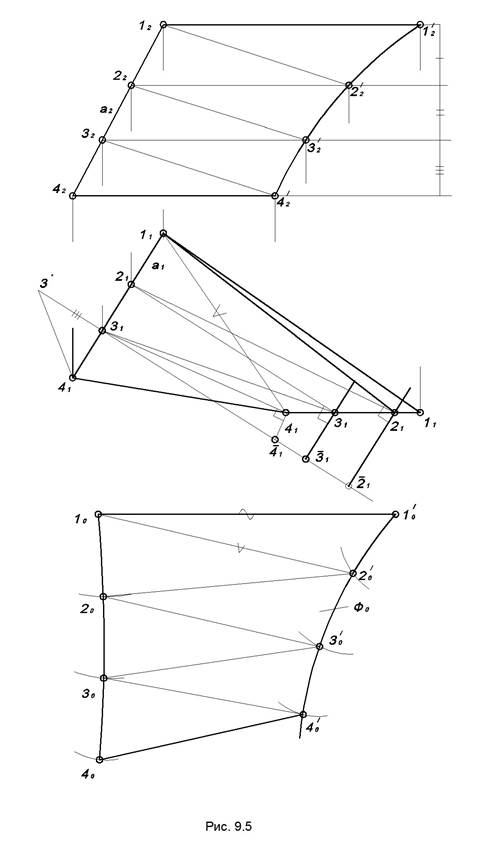
Для построения условных разверток неразвертывающихся поверхностей применяется способ триангуляции. Рассмотрим на примере как строится условная развертка коноида Ф (а,b, П₁) (рис. 9.5).

С помощью образующих делим данную поверхность на части. Каждый из построенных т.о. на поверхности неплоских четырехугольников заменяем парой плоских треугольников, например: 11^’2^’, 12^’2, 22^’3^’, 23^’3 и т.д.

Условную развертку коноида строим как развертку вписанной многогранной поверхности, гранями которой являются треугольники 11^’2^’, 12^’2, 22^’3^’, 23^’3, 33^’4^’, 34^’4. Стороны этих треугольников 11^’, 22^’, 33^’, 44^’ на горизонтальную плоскость проецируются в натуральную величину. Натуральные величины остальных сторон треугольников можно определить методом прямоугольного треугольника.

По трем сторонам строим первый треугольник 1₀1₀^’2₀^’, к которому последовательно пристраиваем остальные. Соединив вершины ограничивающих ломанных плавными кривыми, получим условную развертку коноида Ф₀.

Поверхности вращения общего вида относятся к классу неразвертывающихся. Поэтому для таких поверхностей строят условные развертки. Метод получения указанных разверток заключается в следующем. Рассматриваемую поверхность приближенно заменяют несколькими касками развертывающихся линейчатых поверхностей, вписанных в данную поверхность или описанных около нее. Линейчатые поверхности, в свою очередь, аппроксимируют многогранными поверхностями. Совокупность разверток этих многогранных поверхностей и принимают условно за развертку неразвертывающейся поверхности вращения.

Условную развертку поверхности вращения можно получить способом вспомогательных цилиндров. Как видно из самого названия, этот способ заключается в замене поверхности вращения другой поверхностью, состоящей из участков цилиндрических поверхностей.

Для примера построим развертку сферы способом вспомогательных цилиндров (рис. 9.6). Построения выполним в следующем порядке:

1. Разделим заданную поверхность вращения меридианами на некоторое число равных частей – долей. Чем больше долей, тем выше степень приближения.

2. Каждую долю заменим участком описанной цилиндрической поверхности, у которой направляющая – средний полумеридиан доли, а образующие перпендикулярны направляющей.

Цилиндрическая поверхность касается заданной поверхности вращения в точках среднего полумеридиана доли. Границами для участка цилиндрической поверхности служат линии пересечения плоскостей меридианов, ограничивающих рассматриваемую долю, с соответствующей цилиндрической поверхностью.

3. Каждый участок цилиндрической поверхности целесообразно развернуть способом нормального сечения, заменяя цилиндрическую поверхность поверхностью призмы.

Рассмотрим последовательность построения условной развертки четвертой части сферы, например, участок между меридианами a и b. Чтобы условная развертка сферы была выполнена с большим приближением к самой сфере, следует делить сферу на 12 долей. Но в данном случае предпринята грубая аппроксимация с целью сделать наглядными все построения. Средний меридиан m доли (нормальное сечение аппроксимирующей цилиндрической поверхности) спрямляем методом малых хорд.

Участки параллелей k, k^’, k^” и т.д. заменим отрезками касательных t, t^’, t^” и т.д., которые являются образующими цилиндрической поверхности. Отрезки образующих проецируются без искажения на П₁.

Меридиан m на развертке спрямляется в отрезок 1₀7₀. Через точки 2₀3₀4₀5₀6₀ проводим прямые, перпендикулярные 1₀7₀, которые соответствуют образующим цилиндра.

На уровне точки 2₀ ширина доли развертки равна отрезку t₁^”, на уровне точки 3₀ - t₁^’ и т.д. Концы этих отрезков соединим плавными кривыми и получим условную развертку одной доли поверхности вращения. Скопировав полученную фигуру по количеству долей, получим полную условную развертку сферы. Аналогично можно выполнить развертку любой поверхности вращения.

Условную развертку поверхности вращения можно построить также способом вспомогательных конусов. На рис. 9.7 поверхность вращения аппроксимирована отсеками двух конических поверхностей и одной цилиндрической и построены развертки этих трех отсеков. В связи с тем, что рассмотренная поверхность симметрична, можно построить развертку одной ее половины.

10. Аксонометрические проекции

Понятие о процессе формирования аксонометрической проекции дано в разделе 1.3. Рассмотрим подробнее некоторые свойства аксонометрических проекций и способы построения наиболее распространенных на практике видов аксонометрических проекций.

10.1 Коэффициенты искажения

При проецировании координатных осей на аксонометрическую плоскость масштабные отрезки проецируются с некоторым искажением, если координатные оси не параллельны аксонометрической плоскости. Пусть единичный отрезок е на оси Ох проецируется на аксонометрическую плоскость в отрезок : единичный отрезок на оси у – в отрезок , на оси z - . Тогда отношения:

U = , V = , W = 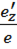называются коэффициентами искажения.

Обычно на практике аксонометрические координатные отрезки измеряют натуральным масштабом е. Поэтому построение аксонометрического чертежа проводится не по аксонометрическим масштабам , , , а по заданным искажениям U, V, W.

10.2 Основная теорема аксонометрии

Меняя положение прямоугольной декартовой системы координат относительно аксонометрической плоскости и направления проецирования, можно получать множество различных вариантов положения аксонометрических осей (исключая случайные их совпадения) и различные аксонометрические масштабы. Поэтому возникает вопрос о том, возможно ли произвольно выбрать аксонометрические оси и масштабы.

Ответ на этот вопрос дает теорема Польке.

Всегда найдется такое положение прямоугольной декартовой системы координат в пространстве и такой единичный масштабный отрезок, а также такое направление проецирования, что любая аксонометрическая система окажется параллельной проекцией данной системы координат.

Следовательно, различных аксонометрических проекций существует бесконечное множество, но на практике обычно пользуются только некоторыми из них.

10.3 Основные виды аксонометрических проекций

Выбор аксонометрических проекций детали обусловлен различными требованиями, основными из которых являются наглядность и простота построения.

ГОСТ 2.317 – 69 устанавливает следующие виды аксонометрических проекций. (рис. 10.1)

Самыми наглядными из перечисленных аксонометрий являются прямоугольная изометрия и прямоугольная диметрия. В дальнейшем подробнее рассматривается простая в построении и самая наглядная прямоугольная изометрия. Косоугольные фронтальная и горизонтальная изометрии менее наглядные, но очень просты при изображении деталей, которые содержат большое количество окружностей, расположенных в параллельных между собой плоскостях.