Высшего профессионального образования 4 страница

Следующие две теоремы приведены без доказательства.

Теорема 3 (теорема Монжа). Если две квадрики описаны около третьей (или вписаны в нее), то линии их пересечения распадается на две коники.

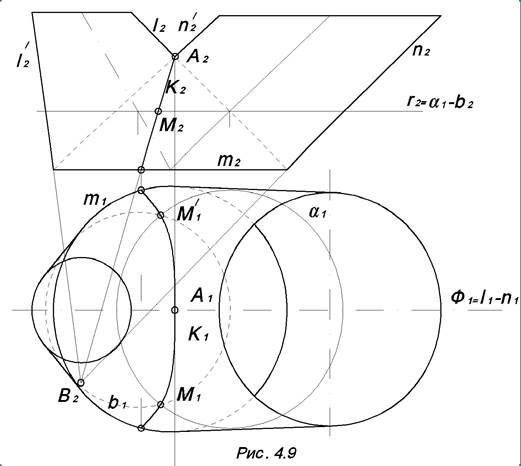
На рис. 4.10 конус и цилиндр описаны около сферы, следовательно, линией их пересечения являются две коники m и n, причем, их фронтальные проекции m₂ и n₂ – отрезки прямых, т.к. общая плоскость симметрии Ф данных поверхностей параллельна П₂. Общими точками данных поверхностей являются точки А, В, С, которые построены с помощью вспомогательной плоскости Ф.

Особыми точками искомой линии пересечения являются точки К и К^’. Эти точки строятся как точки пересечения окружностей касания a и b сферы к конусу и цилиндру. Особенность точек К и К^’ обусловлена тем, что это точки прикосновения данных поверхностей и принадлежат каждой из линий m и n. Горизонтальные проекции линий m и n следует строить по принадлежности к одной из данных поверхностей.

Замечание. Точкой прикосновения двух поверхностей называется точка, через которую можно провести общую касательную плоскость к этим поверхностям.

Теорема 4. Линия пересечения двух квадрик, имеющих двойное прикосновение, распадается на две коники, которые проходят через точки прикосновения.

На рис. 4.11 показан пример, иллюстрирующий эту теорему.

Сфера и эллиптический конус имеют две точки соприкосновения А и А^э, следовательно, линия их пересечения распадается на две коники m и n, их профильные проекции – отрезки m₃ и n₃, т.к. общая плоскость симметрии Р параллельна П₃. m € А, n € А. Горизонтальная и фронтальная проекции этих линий строятся по принадлежности сфере или конусу.

В данном случае линии m и n – окружности, т.к. они являются плоскими кривыми, принадлежащими сфере. Плоскости, параллельные плоскости одной из этих окружностей, пересекают данный эллиптический конус по окружностям. Т.о., поверхность эллиптического конуса содержит два семейства окружностей. Аналогично можно построить круговые сечения на любой квадрике, кроме косой плоскости и гиперболического и параболического цилиндроидов и конусов.

5. Метод вращения

В разделе 1.6 рассмотрен метод замены плоскостей проекций.

Не менее важным является и метод вращения. Большинство задач, в которых применяется метод замены плоскостей проекций, могут решены и методом вращения. На выбор того или иного метода влияют требования компактности чертежа, простоты построения, наглядности и др. факторы.

При применении метода вращения положение плоскостей проекций не изменяется, а перемещается геометрический объект. Перемещение геометрического объекта достигается посредством вращения его вокруг некоторой оси. В качестве оси вращения обычно выбирают проецирующую прямую или прямую, параллельную одной из плоскостей проекций.

Следует помнить, что в процессе вращения вокруг оси вращающаяся точка описывает окружность, расположенную в плоскости, перпендикулярной оси вращения i. Центр окружности принадлежит оси вращения. Все точки геометрического объекта поворачиваются на один и тот же угол u. Точки, принадлежащие оси вращения, остаются неподвижными (рис. 5.1).

Вращение вокруг проецирующей прямой рассмотрим на примере вращения точки.

Задача. Повернуть точку вокруг горизонтально проецирующей прямой i на угол u, u = 60⁰ (рис 5.2).

Плоскость, в которой перемещается точка при вращении, перпендикулярна оси вращения i, следовательно, параллельна плоскости П₁. Значит, на плоскость П₁ дуга окружности, которая является траекторией движения точки, спроецируется в натуральную величину. Это же можно сказать и про угол поворота.

Центр дуги принадлежит оси вращения, следовательно, горизонтальная проекция центра дуги – точка i₁.

Плоскость вращения точки перпендикулярна фронтальной плоскости проекций, следовательно, фронтальная проекция этой дуги – отрезок прямой, перпендикулярной i₂.

Итак, k₁ и k₂ – проекции траектории вращения точки А. На k₁ от точки А₁ следует отложить отрезок дуги, равный 60⁰. А^’ – искомая точка, фронтальная проекция ее определяется по принадлежности k.

Аналогично можно рассмотреть вращение вокруг фронтально проецирующей прямой.

Метод вращения для более сложных задач можно применять неоднократно, а также в сочетании с методом замены плоскостей проекций. Например, если ось вращения прямая общего положения, то следует, посредством метода замены плоскостей проекций, преобразовать ее в прямую частного положения и затем выполнить вращение.

6. Пересечение линии и поверхности

Для определения точек пересечения линии и поверхности необходимо выполнить следующие действия:

· Через данную линию провести вспомогательную поверхность

· Построить линию пересечения вспомогательной поверхности с данной

· Точки пересечения полученной кривой с данной являются искомыми точками пересечения линии и поверхности.

Если данная кривая является прямой линией, то в качестве вспомогательной поверхности целесообразно выбирать проецирующую плоскость или, в некоторых случаях, плоскость общего положения. Иногда полезно при решении задач пользоваться методами преобразования поверхностей.

Задача. Найти точки пересечения прямой l со сферой, определить видимость прямой (рис. 6.1).

1. Через прямую l проведем фронтально проецирующую плоскость ∑.

2. Плоскость пересекает сферу по окружности К, горизонтальная проекция которого эллипс k₁. (Эллипс k₁ можно построить по большой А₁А₁^’ и малой В₁С₁ осям или по отдельным точкам, которые строятся на линиях каркаса).

3. Точки M и N пересечения кривой k с прямой l являются искомыми.

4. Для определения видимости прямой следует оценить сначала видимость точек M и N. По горизонтальной проекции видно, что точка М расположена на ближней половине сферы, следовательно, на фронтальной проекции она видимая, точка N на фронтальной проекции невидимая, т.к. расположена на дальней половине сферы. Аналогично по фронтальной проекции определяется видимость точек М и N на горизонтальной проекции. Отрезок MN находится внутри сферы, поэтому невидимый на любой проекции. Видимость прямой вне этого отрезка совпадает с видимостью рассмотренных точек. Например, на горизонтальной проекции отрезок прямой правее точки М закрывается сферой.

В этой задаче l является прямой общего положения, поэтому плоскость ∑ не параллельна плоскости П₁, и проекция окружности k₁ – эллипс. Построение эллипса проводится приближенно, следовательно, приближенным является и решение задачи на рис. 6.1.

Задачу можно решить точнее, если выбрать дополнительную плоскость проекции П₄ параллельно плоскости ∑ (рис. 6.2), тогда окружность k на П₄ спроецируется в окружность k₄, l₄ строится по точкам 1 и 2. K₄ П l₄ = М_4, N_4.

Если прямая l пересекает ось вращения данной поверхности, то для решения задачи целесообразно воспользоваться методом вращения (рис. 6.3).

1. Повернем прямую l вокруг оси i так, чтобы она стала фронтальной прямой l^’. (Для этого достаточно повернуть некоторую точку А, а точку В остается неподвижной, т.к. принадлежит оси вращения). На тот же угол и вокруг той же оси поворачивается сфера. Очевидно, что ее изображение на чертеже не изменятся. Найти точки пересечения прямой l^’ со сферой просто, т.к. вспомогательная плоскость ∑^’ (∑^’ € l^’ и ∑^’ ┴ П₁) пересекает сферу по главному меридиану m.

m П l^’ = M^’ : N^’.

Вращая сферу и прямую l в противоположном направлении, следует вернуть их в первоначальное положение. Тогда точка M^’ и N^’ на прямой l займут положения М и N.

При построении точек пересечения прямой с цилиндрическими или коническими поверхностями вспомогательную поверхность можно выбрать так, чтобы она пересекала данную поверхность по прямым. Такая плоскость в общем случае является плоскостью общего положения, но пользоваться ею целесообразно, т.к. удается избежать построения кривых линий. Следует заметить, что направляющей поверхности в этом случае должна быть плоская кривая.

Задача. Найти точки пересечения прямой l с конической поверхностью Ф. Определить видимость прямой.

На рис. 6.4 показано решение этой задачи с помощью вспомогательной плоскости частного положения.

1. ∑ € l; ∑ ┴ П.

2. ∑ П Ф = к. (Для построения к здесь воспользовались каркасом данной поверхности, который состоит из прямолинейных образующих).

3. к П l = М,N

4. Определить видимость l.

На рис. 6.5 задача решена посредством вспомогательной плоскости, проходящей через вершину конуса и прямую l.

1. Q (l,S) – вспомогательная плоскость.

2. Построим линии пересечения Q с конусом Ф. Для этого следует выполнить следующие действия:

· А – любая точка прямой l. Через вершину конуса S и точку А проведем прямую m, т.е. плоскость Q теперь задана пересекающимися прямыми l и m.

· ∑ - плоскость, проходящая через направляющую к данной поверхности.

∑ П Q = (12)

(12) П а = В,С.

SB и SC – прямые пересечения плоскости Q с конусом.

3. SB П l = M;

SC П l = N/

M и N – искомые точки.

В случае задания цилиндрической поверхности прямую m следует проводить параллельно образующим этой поверхности.

7. Математическая модель линии пересечения поверхностей второго порядка

Геометрические и аналитические модели и алгоритмы, рассмотренные в этом курсе, могут быть использованы при согласовании программ для решения многих геометрических и специальных задач на ЭВМ.

Например, задача на построение линии пересечения поверхностей второго порядка.

Общее уравнение квадрики имеет вид:

a₁₁x² + a₂₂y² + a₃₃z² + a₁₂xy + a₁₃xz + a₂₃yz + a₁x + a₂y + a₃z + a₀ = 0

Если коэффициенты этого уравнения не равны нулю, то уравнение квадрики, плоскость симметрии которой являются плоскости общего положения. На практике чаще встречаются задача, в которых плоскости симметрии поверхностей параллельны плоскостям проекций. В обобщенном уравнении таких поверхностей некоторые коэффициенты равны нулю или связаны определенным отношением. Например, трехосный эллипсоид, однополостный гиперболоид, эллиптический параболоид, конус и цилиндр могут быть описаны таким уравнением:

+ + К + P (z – z₀) = D

Коэффициенты этого уравнения имеют определенный геометрический смысл. Вид квадрики зависит от значений коэффициентов Р, К и D, размеры от значений А, В, и С и положение относительно координатных плоскостей от х₀, у₀, z₀.

Возможны следующие частные случаи.

1. При Р = 0, К = 1, D = 1, уравнение имеет вид:

- - = 1

Это уравнение трехосного эллипсоида, у которого х₀, у₀, z₀ – координаты центра; А, В, С – соответствуют значениям длин полуосей.

Если А=В=С, то это уравнение сферы, радиус которой равен А.

2. При D =1, К = -1, Р = 0, уравнение имеет вид:

+ - = 1

Это уравнение эллиптического однополостного гиперболоида, у которого х₀, у₀, z₀ – координаты центра гиперболы; А и В соответствуют значениям длин полуосей горловины рассматриваемой поверхности; С – значение мнимой полуоси гиперболы (главного меридиана) (рис. 3.7.3)

3. При D = 0, К = -1, Р = 0, уравнение имеет вид:

- - = 0

Это уравнение эллиптического конуса, у которого х₀, у₀, z₀ – координаты вершины конуса; А и В полуоси направляющего эллипса (основания конуса); С – высота конуса. Если А=В, то это уравнение конуса вращения.

4. При D = 1, К = 0, Р = 0, уравнение имеет вид:

+ = 1

Это уравнение эллиптического цилиндра, поверхность которого является горизонтально проецирующей; х₀, у₀, z₀ – координаты центра направляющего эллипса, причем z может быть любое; А и В – значение полуосей направляющего эллипса.

5. При D = 0, К = 0, Р = -1, уравнение имеет вид:

+ = + (z – z₀₎

Это уравнение эллиптического параболоида, у которого х₀, у₀, z₀ – координаты вершины; А и В – значение полуосей горизонтали расположенной на расстоянии h = 1 от вершины параболоида. Если h = h₀, то значение А и В можно определить по формулам:

А = ; В = ;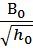

Где А₀ и В₀ соответствуют значениям полуосей параллели на высоте h₀.

Если р = -1, то ветви параболы (меридианов поверхности) направлены вверх, если р = 1, то вниз.

Расшифровка значений необходимых коэффициентов показана в таблице 7.1

Таблица 7.1

	Сфера	Трехосный эллипсоид	Однополостный параболоид	Эллиптический конус	Эллиптический цилиндр	Эллиптический параболоид
x	x0	x0	x0	x0	x0	x0
y	y0	y0	y0	y0	y0	y0
z	z0	z0	z0	z0	z0 – любое	z0
А	R сферы	А полуось по оси х	А полуось по оси х	А полуось по оси х	А полуось по оси х	А =
В	R сферы	В – полуось на оси у	В – полуось на оси у	В – полуось на оси у	В – полуось на оси у	В =
С	R сферы	С – полуось на оси z	С – мнимая ось	0 - высота	Любое действительное не равное 0	Любое действительное не равное 0
D
K			-1	-1
P						≠ 1

Математической моделью линии пересечения поверхностей является система уравнений, описывающих данные поверхности. Чтобы получить уравнение горизонтальной проекции линии пересечения, следует решая эти уравнения совместно, исключить z, а для фронтальной проекции – у.

При разработке алгоритма для машинного решения задачи этот путь зачастую не является рациональным из-за сложности уравнений проекций линии пересечения. Поэтому следует воспользоваться геометрическим алгоритмом построения линии пересечения поверхностей, изложенного в главе 4.

Например, по заданным значениям параметров D, K, Р, А, В, С, х₀, у₀, z₀ получены уравнения двух квадрик:

+ + К + P (z – z₀) = D;

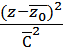+ + К + (z – ) = .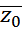

Задавая значения z = z_n, получим уравнения двух коник. В рассмотренных случаях это – уравнения эллипсов, оси симметрий которых принадлежат прямой, параллельной оси Оx. Следовательно, их совместное решение сводится к решению уравнения второго порядка, в результате которого определяются координаты точек линий пересечения. Варьируя z_n можно получить достаточное количество точек этой линии.

Замечание. В тех случаях, когда общая плоскость симметрии данных поверхностей не параллельна плоскости проекций, прежде чем определить параметры х₀, у₀, z₀, полезно применить метод замены плоскостей проекций (раздел 1.6), выбирая дополнительную плоскость проекции параллельно общей плоскости симметрии и задачу решать в новой системе плоскостей проекции и связанной с ней системе координат.

Аналогично составляются алгоритмы для построения линии пересечения с помощью ЭВМ двух любых поверхностей, имеющих математические модели. Причем в некоторых случаях не обязательно составлять уравнение данной поверхности, а можно ограничиться заданием уравнений линий, входящих в определитель поверхности.

8. Метрические задачи

Кроме позиционных задач в технической практике приходится решать задачи, в которых выясняется вопрос измерения отрезков и углов, определения натуральной величины или формы плоских фигур и т.д. Такие задачи называются метрическими. При их решении существенную роль играют условия перпендикулярности прямых и плоскостей на комплексном чертеже.

8.1 Условия перпендикулярности на комплексном чертеже

Эти условия основаны на следующей теореме об ортогональной проекции прямого угла.

Для того, чтобы ортогональной проекцией прямого угла был прямой угол, необходимо и достаточно, чтобы, по крайней мере, одна из сторон этого угла была параллельна плоскости проекций, при этом другая сторона не должна быть перпендикулярна этой плоскости.

Доказательство этой теоремы непосредственно следует из теоремы из трех перпендикулярах.

Значит, если одна сторона прямого угла является прямой уровня, то прямой угол проецируется без искажения на плоскость, параллельную этой стороне. Зная это, выведем свойства проекций перпендикуляра к плоскости.

Известно, что прямая, перпендикулярная плоскости, перпендикулярна к любой прямой этой плоскости. Поэтому, если некоторая прямая перпендикулярна плоскости, то она перпендикулярна горизонтали h к фронтали f этой плоскости. А эта перпендикулярности сохраняется при ортогональном проецировании: для горизонтали – на горизонтальную плоскость, для фронтали – на фронтальную плоскость.

Т.о., прямая и плоскость общего положения взаимно перпендикулярны в том и только том случае, когда проекции прямой перпендикулярны одноименным проекциям соответствующих линий уровня, т.е. горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали.

Рассмотрим примеры построе6ния прямой, перпендикулярной плоскости; плоскости, перпендикулярной прямой, и взаимно перпендикулярных плоскостей.

Задача. Через точку М провести прямую n, перпендикулярную плоскости О (А, В, С) (рис. 8.1).

1. Проводим в плоскости О горизонталь h (h₁, h₂).

2. Горизонтальная проекция перпендикуляра n₁ ┴ h_1, n₁ € M₁

3. Проводим в плоскости О фронталь Р (f₁, f₂)

4. Фронтальная проекция перпендикуляра n₂ ┴ f_2, n₂ € M₂

П₁ и П₂ – проекции искомого перпендикуляра n.

Задача. Через точку А провести плоскость О, перпендикулярную прямой l (рис. 8.2)

Для построения плоскости О, перпендикулярной к плоскости А можно провести двумя путями:

1. Плоскость О проводится через прямую, перпендикулярную к плоскости Л.

2. Плоскость О проводится перпендикулярно к прямой, принадлежащей плоскости Л или параллельной этой плоскости.

Задача. Через прямую l провести плоскость О, перпендикулярную плоскости Л (АВС) (рис.8.3)

1. На прямой l выберем любую точку К.

2. Через точку К проводим прямую n, перпендикулярную плоскости Л. Искомая плоскость определена пересекающимися прямыми l и n.

Чтобы через данную точку провести плоскость перпендикулярную к двум данным плоскостям, следует через эту точку провести прямые перпендикулярные к каждой из данных плоскостей, или построить линию пересечения данных плоскостей, тогда искомая плоскость перпендикулярна к этой линии.

При решении задач на построение с использованием свойств перпендикулярности прямой и плоскости необходимо в каждом конкретном случае в результате анализа исследуемых объектов определить ортогональные элементы и их расположение.

1. В прямоугольном треугольнике прямой угол между катетами.

2. У квадрата и прямоугольника прямые углы при вершинах.

3. Диагонали ромба взаимно перпендикулярны и делятся в точке пересечения пополам.

4. В равнобедренном треугольнике совпадают высота, биссектриса и медиана, проведенные из его вершины между равными сторонами.

В некоторых задачах полезно применять свойства множеств геометрических объектов, основанные на признаке перпендикулярности:

1. Плоскость, перпендикулярная прямой, есть множество прямых, перпендикулярных данной в заданной точке.

2. Плоскость, перпендикулярная к отрезку и проведенная через его середину, есть множество точек, равноудаленных от концов этого отрезка.

Задача. Достроить горизонтальную проекцию прямоугольного треугольника АВС, если дана его фронтальная проекция и горизонтальная проекция его катета АВ. Угол В – прямой (рис. 8.4). Множество всех прямых, проходящих через точку В и перпендикулярных отрезку АВ, образуют плоскость О┴АВ. На чертеже эту плоскость зададим горизонталью h и фронталью f. С € О и С₁ следует строить по принадлежности плоскости О.

8.2 Способы решения некоторых метрических задач

Зачастую метрические задачи можно решить несколькими способами. Во многих случаях рационального решения добиваются, применяя способы преобразования комплексного чертежа. Рассмотрим это на нескольких примерах.

Задача. Определить длину отрезка АВ.

1 способ. Применим метод замены плоскостей проекций (рис. 8.5). Дополнительную плоскость проекций П₄ (П₄┴П₁) следует провести параллельно прямой АВ. А₁ В₁ проекция АВ на П₄. Очевидно, что /А₄В₄/ = /АВ/.

2 способ. Решим задачу методом вращения вокруг проецирующей оси (рис. 8.6). Через один из концов отрезка (например В) следует провести ось вращения i (i ┴П₁) и повернуть отрезок вокруг оси так, чтобы он стал параллелен плоскости П₂. Горизонтальная проекция траектории движения точки А – дуга окружности а, фронтальная проекция – отрезок а₂ (а₂┴ i). После поворота отрезок занял положение В₂^’А₂^’, / А₂^’ В₂^’/ = /АВ/.

3 способ. Способ прямоугольного треугольника.

Проанализируем рассмотренные в предыдущих способах чертежи. На рис. 9.7 отрезок А₄В₄ является гипотенузой прямоугольного треугольника А₄К₄ В₄, у которого катет В₄К₄ равен горизонтальной проекции отрезка А₁В₁, а второй катет равен разности расстояний концов отрезков до горизонтальной плоскости проекций. Такой же вывод можно сделать, рассматривая треугольник В₂^’K₂^’A₂^’ на рис. 8.6.

Поэтому, не проводя дополнительных построений, длину отрезка можно определить, построив прямоугольный треугольник как показано на рис. 8.7. Прямоугольный треугольник можно построить также на свободном поле чертежа.

4 способ. Расчетно – графическая модель (рис. 8.8)

В тех ситуациях, когда рассматриваемую задачу необходимо решать многократно, полезно, обобщая полученные результаты, составить расчетно – графическую модель.

Если всевозможные прямоугольные треугольники с равными гипотенузами расположить так, чтобы один конец гипотенузы совпадал с точкой (0,0), а один из катетов каждого треугольника принадлежал одной прямой, то второй конец гипотенузы должен принадлежать окружности с радиусом, равным гипотенузе.

На рис. 8.8 построено множество таких окружностей, с числовыми отметками, соответствующими радиусами. Полученный чертеж следует дополнить двумя семействами параллельных прямых. Числовые отметки вертикальных прямых соответствуют длинам одной из проекций отрезка, а числовые отметки горизонтальных прямых соответствуют величине ∆. Такой чертеж называется расчетно – графической моделью или номограммой.

Порядок ее работы рассмотрим на примере. Пусть длина одной из проекций отрезка равна 4 и ∆ - 3. Находим точку М пересечения вертикальной прямой с числовой отметкой 4 и горизонтальной прямой с числовой отметкой 3. Числовая отметка окружности, проходящей через точку М, определяет искомую длину отрезка.

Задача. Найти расстояние от точки М до плоскости (АВС).