 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Відношення часткового порядку
|
|
Означення 6.1. Відношення  на множині А називають відношенням часткового порядку (або частковим порядком), якщо воно рефлексивне, антисиметричне й транзитивне. Множину А із частковим порядком
на множині А називають відношенням часткового порядку (або частковим порядком), якщо воно рефлексивне, антисиметричне й транзитивне. Множину А із частковим порядком  називають частково впорядкованою множиною й позначають (A,
називають частково впорядкованою множиною й позначають (A,  )
)
Приклад 6.1. Нехай A ={ 1, 2, 3, 4, 5}. Відношення  задамо як звичайне порівняння чисел: (а,b)
задамо як звичайне порівняння чисел: (а,b) 
 тоді й тільки тоді, коли а
тоді й тільки тоді, коли а  b, (а,b
b, (а,b  А). Неважко безпосередньо переконатись, що це відношення є частковим порядком на множині А. ▲
А). Неважко безпосередньо переконатись, що це відношення є частковим порядком на множині А. ▲
Приклад 6.2. Нехай A ={1, 2, 3, 4, 6, 8, 12}. Відношення 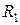 задамо так: (а, b)
задамо так: (а, b) 
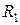 тоді й тільки тоді, коли а ділить b. Отже:
тоді й тільки тоді, коли а ділить b. Отже: 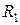 ={(1,1), (2,2), (3,3), (4,4), (6,6), (8,8), (12,12), (1,2), (1,3), (1,8), (1,12), (2,4), (2,6), (2,8), (2,12), (3,6), (3,12), (4,8), (4,12), (6,12)}. Легко переконатись, що це відношення рефлексивне, антисиметричне й транзитивне й, отже, є відношенням часткового порядку на множині А. ▲
={(1,1), (2,2), (3,3), (4,4), (6,6), (8,8), (12,12), (1,2), (1,3), (1,8), (1,12), (2,4), (2,6), (2,8), (2,12), (3,6), (3,12), (4,8), (4,12), (6,12)}. Легко переконатись, що це відношення рефлексивне, антисиметричне й транзитивне й, отже, є відношенням часткового порядку на множині А. ▲
Означення 6.2. Два елементи а та b частково впорядкованої множини (А, R) називають порівняльними, якщо а  b або b
b або b  а. Якщо а та b такі елементи, що ані а
а. Якщо а та b такі елементи, що ані а  b, ані b
b, ані b  а, то їх називають непорівняльними.
а, то їх називають непорівняльними.
Приклад 6.3 Елементи 3 та 4 множини (А, 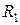 ) із прикладу 6.2 – непорівняльні. ▲
) із прикладу 6.2 – непорівняльні. ▲
Означення 6.3. Якщо (А,  ) частково впорядкована множина, у якій будь–які два елементи порівняльні, то таку множину називають тотально або лінійно впорядкованою, а частковий порядок
) частково впорядкована множина, у якій будь–які два елементи порівняльні, то таку множину називають тотально або лінійно впорядкованою, а частковий порядок  називають тотальним або лінійним порядком. Отже, множина (А,
називають тотальним або лінійним порядком. Отже, множина (А,  ) із прикладу 6.1 лінійно впорядкована, множина (А,
) із прикладу 6.1 лінійно впорядкована, множина (А, 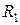 ) із прикладу 6.2 частково впорядкована, але не лінійно впорядкована. Лінійно впорядковану множину називають також ланцюгом.
) із прикладу 6.2 частково впорядкована, але не лінійно впорядкована. Лінійно впорядковану множину називають також ланцюгом.
Приклад 6.4. Нехай А=  – множина всіх булевих векторів довжини п. Визначимо частковий порядок на цій множині так: (а1,а2,..., аn) < (b1,b2,..., bn) тоді й тільки тоді, коли aі
– множина всіх булевих векторів довжини п. Визначимо частковий порядок на цій множині так: (а1,а2,..., аn) < (b1,b2,..., bn) тоді й тільки тоді, коли aі  bі (i =1,2,.. .,п). Цей частковий порядок не є лінійним порядком. Наприклад, не можна порівняти вектори (010000) та (101000). ▲
bі (i =1,2,.. .,п). Цей частковий порядок не є лінійним порядком. Наприклад, не можна порівняти вектори (010000) та (101000). ▲
Матриця відношення часткового порядку. Оскільки відношення часткового порядку є рефлексивним, головна діагональ матриці цього відношення містить одиниці. Через те що воно є асиметричним, жоден одиничний елемент не має симетричного собі відносно головної діагоналі. Оскільки це відношення є транзитивним, наявність одиниць на перетині i -го стовпця та j -го рядка й одиниці на перетині j -го стовпця і k -го рядка спричинює наявність одиниці на перетині i -го стовпця та k- го рядка.
Означення 6.3. У частково впорядкованій множині (А,  ) запис а
) запис а  b означає, що (а, b)
b означає, що (а, b) 
 . Запис а<b означає, що а
. Запис а<b означає, що а  b, але а
b, але а 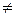 b. Якщо а<b, то кажуть, що а передує b (а менше b) або b виходить з а (b більше а). Елемент b
b. Якщо а<b, то кажуть, що а передує b (а менше b) або b виходить з а (b більше а). Елемент b  А безпосередньо виходить з а
А безпосередньо виходить з а  А тоді й лише тоді, коли а<b і не існує такого c
А тоді й лише тоді, коли а<b і не існує такого c  А, що а < c < b. У такому випадку кажуть також, що елемент а безпосередньо передує елементу b.
А, що а < c < b. У такому випадку кажуть також, що елемент а безпосередньо передує елементу b.
Приклад 6.5. Для відношення часткового порядку  = “ділиться націло на” на множині A= {1, 2, 3, 4, 6, 7, 12, 14, 21, 28} матриця відношення має такий вигляд:
= “ділиться націло на” на множині A= {1, 2, 3, 4, 6, 7, 12, 14, 21, 28} матриця відношення має такий вигляд:
Діаграмма Хассе. Розглянемо частково впорядковану множину (А,  ). Зобразимо кожний елемент
). Зобразимо кожний елемент 
 А точкою
А точкою 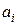 на площині й розглянемо всі впорядковані пари (
на площині й розглянемо всі впорядковані пари (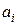 ,
,  ). Зобразимо точку
). Зобразимо точку  вище точки
вище точки 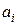 тоді й лише тоді, коли
тоді й лише тоді, коли 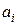 <
<  і з’єднаємо точки
і з’єднаємо точки 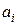 та
та  лінією, якщо
лінією, якщо  безпосередньо виходить з
безпосередньо виходить з 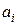 . Результатом процесу є діаграма Хассе: у цій діаграмі існує шлях, який веде від точки
. Результатом процесу є діаграма Хассе: у цій діаграмі існує шлях, який веде від точки 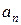 до точки
до точки  , якщо
, якщо 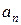 <
<  .
.
Зазначимо, що символ  використовують для позначення довільного відношення часткового порядку.
використовують для позначення довільного відношення часткового порядку.
Елементи частково впорядкованих множин, які мають певні екстремальні властивості, є дуже важливими в багатьох застосуваннях. Елемент частково впорядкованої множини називають максимальним, якщо він не менший від будь-якого елемента цієї множини. Отже, а є максимальним елементом частково впорядкованої множини (А,  ), якщо не існує такого b
), якщо не існує такого b  А, що a<b. Аналогічно, елемент називають мінімальним, якщо він не більший від будь-якого елемента частково впорядкованої множини. Отже, а є мінімальним, якщо не існує такого b
А, що a<b. Аналогічно, елемент називають мінімальним, якщо він не більший від будь-якого елемента частково впорядкованої множини. Отже, а є мінімальним, якщо не існує такого b  А, що b<а. Максимальні та мінімальні елементи легко визначити на діаграмі Хассе – це, відповідно, “верхні” і “нижні” її елементи (“верхні” елементи не мають висхідних ребер, а “нижні” – низхідних).
А, що b<а. Максимальні та мінімальні елементи легко визначити на діаграмі Хассе – це, відповідно, “верхні” і “нижні” її елементи (“верхні” елементи не мають висхідних ребер, а “нижні” – низхідних).
Приклад 6.6. На множині А ={2, 4, 5, 10, 12, 20, 25 } задано відношення часткового порядку  ={(а, b) | а ділить b }. Знайдемо максимальні й мінімальні елементи множини (А,
={(а, b) | а ділить b }. Знайдемо максимальні й мінімальні елементи множини (А,  ). Діаграму Хассе для цієї множини зображено на рис. 6.3. Із цієї діаграми робимо висновок, що максимальні елементи 12, 20 та 25, а мінімальні – 2 та 5. Цей приклад свідчить, що частково впорядкована множина може мати понад один максимальний або мінімальний елемент. ▲
). Діаграму Хассе для цієї множини зображено на рис. 6.3. Із цієї діаграми робимо висновок, що максимальні елементи 12, 20 та 25, а мінімальні – 2 та 5. Цей приклад свідчить, що частково впорядкована множина може мати понад один максимальний або мінімальний елемент. ▲

Рис. 6.1. Діаграма Хассе
Дата публикования: 2015-09-17; Прочитано: 3059 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
