 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Ускорение жидкой частицы
|
|
Проекции ускорения  жидкой частицы на оси x, y, z будут иметь вид
жидкой частицы на оси x, y, z будут иметь вид  ,
, 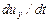 и
и  . Для проекции производной скорости на ось
. Для проекции производной скорости на ось  , которая является функцией четырех аргументов x, y, z и
, которая является функцией четырех аргументов x, y, z и  , запишем
, запишем
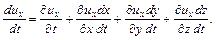 (3.26)
(3.26)
Величины производных от координат по времени могут быть переписаны как
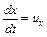 ;
; 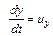 ;
; 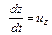 , (3.27)
, (3.27)
поэтому
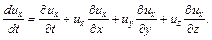 (3.28)
(3.28)
Аналогичные соотношения можно получить и для функций 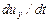 и
и  .
.
Слагаемые 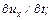
 ;
; 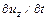 являются локальными ускорениями в данной точке жидкости.
являются локальными ускорениями в данной точке жидкости.
Компоненты 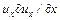 ,
, 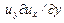 ,
, 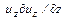 характеризуют изменение компонент скорости при прохождении частицы через данную точку и называются конвективными ускорениями.
характеризуют изменение компонент скорости при прохождении частицы через данную точку и называются конвективными ускорениями.
Уравнениям для проекции ускорения на ось  с использованием двучлена
с использованием двучлена
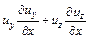 (3.29)
(3.29)
можно придать вид
 (3.30)
(3.30)
Конвективные составляющие уравнения содержат члены типа 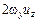 , ответственные за вращение (завихрение) жидкости.
, ответственные за вращение (завихрение) жидкости.
В ряде случаев используется понятие завихренности жидкости с компонентами  ,
, 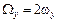 ,
, 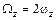 .
.
Дата публикования: 2015-09-17; Прочитано: 471 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
