 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
III. Производная и ее приложения
|
|
Основные правила и формулы дифференцирования:
1. y = c, где c=const,  .
.
2. y = x, y'=1.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8. 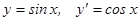 .
.
9.  .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
14.  .
.
15.  .
.
16.  .
.
17. 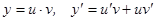 .
.
18.  .
.
19.  - это правило дифференцирования сложной функции.
- это правило дифференцирования сложной функции.
Пример 1. Найти производные  данных функций
данных функций
а)  ; б)
; б)  ;
;
в) 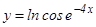 ; г)
; г)  <1;
<1;
д)  ; е)
; е)  .
.
Решение:
а) Применяя правило дифференцирования дроби и формулы (3); (16), имеем

б) Последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, имеем:
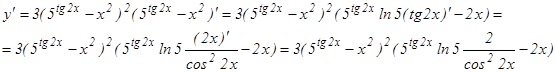
в) 
г) 

д) Предварительно прологарифмируем по основанию е обе части равенства:
 или
или  .
.
Теперь дифференцируем обе части, считая lny сложной функцией от переменной x.
 откуда
откуда
 .
.
е) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную y', надо продифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной y'. Имеем:

Из полученного равенства, связывающего х, у и y', находим производную y':

 откуда
откуда 
Пример 2. Найти производную второго порядка  :
:
а) 
б) 
в) 
Решение: а) Функция у задана в неявном виде. Дифференцируем по х обе части заданного уравнения, считая при этом у функцией от х:
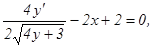 откуда
откуда  (1)
(1)
Снова дифференцируем по х обе части равенства (1):
 (2)
(2)
Заменив y' в (2) правой частью (1), получим
 .
.
б) Найдем первую производную данной функции
 .
.
Найдем производную от первой производной, получим вторую производную функции  :
:

в) Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти производную y', находим сначала дифференциалы dy и dx и затем берем отношение этих дифференциалов:

Тогда 
Производная второго порядка 
 . Значит, чтобы найти y'', надо найти дифференциал dy':
. Значит, чтобы найти y'', надо найти дифференциал dy':

Тогда 
Дата публикования: 2015-09-17; Прочитано: 297 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
