Коэффициент затухания звука в воздухе, дБ/км

Относительная влажность воздуха, %	Среднегеометрические частоты октавных полос, Гц
	0,8 0,4 0,2	1,5 1,3 0,9	3,8 2,8 2,7	12,1 4,9 5,5	9,7

Для звука коэффициент затухания d₀ зависит от частоты звука, температуры, давления и относительной влажности воздуха. При нормальном атмосферном давлении и температуре воздуха, равной +20 °С, значения коэффициента d₀ даны в табл. 6.7. Для электромагнитной волны, распространяющейся в воздухе, d₀» 0 (см. ниже). Следует иметь в виду, что в реальных условиях уровень затухания зависит также от погодных условий (дождь, снег, туман и т. д.), наличия растительности (трава, кустарник, деревья и т. д.), состояния атмосферы (ветер, туман, турбулентность, температурные градиенты и т. д.), наличия отражающих поверхностей (земля, преграды, экраны и т. д.) и ряда других факторов и вычисляется по формуле 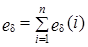, где e_d(i) — уровень затухания при наличии i-го фактора. Если затуханием можно пренебречь (d = 0). то уровень интенсивности:

Диффузное волновое поле в изолированных объемах. Волновое поле называют диффузным, если усредненная по времени объемная плотность энергии w = w_д одинакова во всех точках, а поток энергии через единичную площадку в любой точке и в любом направлении постоянен и равен I_д.

Энергия волны в объеме dV равна de = w_д dV. В диффузном поле эта энергия распределяется равномерно во все стороны пространства 4p. Следовательно, на телесный угол dW = dSсosq/r² приходится часть энергии, равная d²e = w_дcosqd VdS/4pr². В сферической системе координат с полярным углом q элементарный объем dV= r²sinqdqdjdr и полная энергия через площадку dS найдется в результате следующего интегрирования:

Откуда следует, что поток энергии через единичную площадку

(6.31)

Таким образом, поток энергии через единичную площадку в диффузном волновом поле в четыре раза меньше интенсивности I_в бегущих волн с той же объемной плотностью энергии. Для бегущей со скоростью с волны интенсивность I = cw, где w — усредненная объемная плотность энергии. При наличии диффузного поля понятие интенсивности теряет смысл.

Понятие диффузного поля часто используют при определении плотности потока энергии I_п в изолированных объемах. Под изолированным объемом понимается пространство, огражденное стенками (например, производственное помещение, кабина, пространство под кожухом машины и т. д.). Волны в изолированных объемах, многократно отражаясь, образуют поле, которое изменяется при изменении геометрических размеров, формы и других характеристик источника.

Волновое поле в каждой точке изолированного объема можно представить в виде совокупности волн, непосредственно приходящих в эту точку от источника, именуемую как прямая волна, и совокупности болн, попадающих в нее после отражений от границ изолированного oбъема — отраженная волна.

Плотность энергии w_п в любой точке изолированного объема будет складываться (рис. 6.38) из плотности энергии w прямой волны и плотности энергии w_д при диффузном поле отраженной волны: w_п = w + w_д. Умножив это уравнение на скорость с, получим

I_п = I + 4I_д

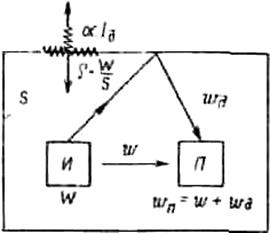
Рис. 6.38. Диффузное поле отраженной волны

Интенсивность прямой волны в общем случае определяется формулой (6.28). Выразим плотность потока энергии I_д через мощность источника. При работе источника в изолированный объем постоянно поступает энергия. При мощности источника W отраженный от границ полный поток энергии составит r W, а от единичной площадки r W/S. За единицу времени через единичную площадку границы вследствие поглощения исчезнет количество энергии, равное aI_д. Так как в диффузном поле плотность энергии постоянная, то должно соблюдаться равенство r W/S = aI_д. Для простоты дальнейших рассуждений здесь предполагается, что коэффициент a значительно больше коэффициента t. Уравнение (6.32) принимает вид

(6.33)

Из полученного выражения видно, что в изолированном объеме плотность потока энергии получает некоторое приращение, которое аналитически обусловлено наличием множителя (1 - a)/a, который велик при коэффициенте a близком к нулю.

Защитное устройство бесконечной толщины. Во многих случаях информацию можно получить, исследуя вместо реальной конструкции теоретическое защитное устройство бесконечной толщины, оно представляет собой просто среду, бесконечно простирающуюся в направлении распространения волны. Таким образом, волна из одной среды проходит в другую среду (защитное устройство), предварительно попадая на границу раздела этих сред. При падении на плоскую границу раздела двух разных сред плоская волна частично отражается, частично проходит в другую среду, оставаясь плоской, но меняя при этом свое направление распространения, т. е. преломляясь. Таким образом, в общем случае существуют три волны: падающая, отраженная и преломленная (прошедшая).

При прохождении границы раздела сред без поглощения должен соблюдаться закон сохранения энергии: W^- + W^~ = W⁺. Кроме того, на границе должны выполняться специфические для волн данной природы условия: например, для звуковых волн по обе стороны границы должны быть равны звуковые давления — принцип непрерывности звукового давления; для электромагнитных волн на границе раздела двух сред непрерывны тангенциальные составляющие электромагнитного поля. Условие непрерывности при нормальном падении волн можно записать в виде равенства на границе амплитуд поля в среде i и среде j: [u_m]_j = [u_m]_i Усредненный поток энергии можно выразить через интенсивность: W= IS, а интенсивность — через амплитуду и импеданс среды с помощью формулы (6.25). Тогда закону сохранения энергии можно придать вид (рис. 6.39)

где и⁺_m, u^- _т, и u^~ _т — амплитуда, соответственно, падающей, отраженной и прошедшей волн, а z^S_k = z_k/S_k — импеданс на единицу площади (k = i, j).

В среде i существуют падающая и отраженная волна, которые на границе создают суммарную амплитуду [u_m]_j = и⁺_m + и^-_m в среде j существует только преломленная волна: [u_m]_j = u^~_m. Условие непрерывности и закон сохранения энергии позволяют найти амплитудный коэффициент отражения R_ij и амплитудный коэффициент передачи Т_ij при пялении волны на границу (i,j ) из среды i:

(6.34)

Рис. 6.39. Баланс энергии на границе раздела сред

При этом имеем Т_ij = 1 + R_ij, R_ij = - R_ij. Так как значение коэффициента отражения лежит между -1 и +1, то значение коэффициента передачи заключено в интервале от 0 до 2 и он всегда положителен. При равных площадях (S_i = S_j) соотношения (6.34) примут такой же вид, который можно получить простой заменой z^S_k на z_k а при равных импедансах сред (z_i = z_j) — заменой z^S_k на 1/S_k (k = i, j ). Амплитудные коэффициенты отражения и передачи при нормальном падении волн связаны с соответствующими энергетическими коэффициентами соотношениями:

Защитное устройство конечной толщины. В общем случае защитное устройство имеет конечную толщину. При этом волна, падая на защитное устройство, частично отражается, а частично может проходить сквозь него. Отражательную способность защитного устройства характеризуют коэффициентом отражения энергетическим и амплитудным. Прозрачные свойства защитного устройства характеризуют соответствующими коэффициентами передачи. Амплитудные коэффициенты отражения и передачи на границах разных сред будем обозначать соответственно через R_ij и Т_ij. Эти величины определены соотношениями (6.34). Амплитудные коэффициенты отражения и передачи защитного устоойства будем обозначать соответственно чеоез R и Т. при этом в комплексной форме

где и — соответственно амплитуда падающей и отраженной волны на входе в защитное устройство; — амплитуда волны на выходе из защитного устройства.

Рассмотрим случай, когда гармоническая волна падает из среды 1 (рис. 6.40) на защитное устройство произвольной толщины h, состоящее из среды 2, ограниченной с другой стороны средой 3, при этом S₁ = S₂ = S₃. Примем, что импедансы сред соответственно равны z₁, z₂ и z₃, а волновое поле в среде 2 на длине h затухает по экспоненциальному закону , где k̂_* — коэффициент распространения. При неравных импедансах сред часть энергии на границе (1, 2) отражается обратно в среду 1 в соответствии с формулой (6.34). Амплитуда падающей волны равна и⁺_m. Обозначив амплитуду отраженной волны через u̇₂, имеем: u̇₂ = R₁₂ и̇⁺_m.

Рис. 6.40. Схема защитного устройства конечной толщины

Другая часть энергии пройдет в среду 2 и, изменившись пропорционально коэффициенту передачи T₁₂ на границе (1, 2), претерпит в среде 2 затухание по закону , так что амплитуда волны в среде 2, которую обозначим через u̇₁, определится выражением . Эта волна на границе (2, 3) частично отразится и создаст в среде 2 отраженную волну, амплитуда которой с учетом затухания станет равной 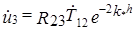и частично пройдет в среду 3. Амплитуда прошедшей волны будет pавна . Волна с амплитудой u̇₃ частично пройдет в среду 1: , а частично отразится от границы (1, 2) -и снова будет распространяться в среде 2 в виде волны с амплитудой . Процесс отражения и прохождения волн на границе сред (1, 2 и 2, 3) будет продолжаться до полного затухания волн. Суммируя все волны, из которых в среде 1 формируется общая отраженная волна, можно получить для амплитуды этой волны следующее выражение:

(6.37)

где z₁₂ = z₁/z₂ и z₃₂ = z₃/z₂. Полученные соотношения носят общий характер, и их можно применять при решении задач защиты гак от звуковых, так и от электромагнитных полей.

Если по обе стороны от защитного устройства находится одна и та же среда, то импедансы z₁ и z₃ равны. Тогда формулы (6.36) и (6.37) преобразуются к виду:

Амплитудные коэффициенты R и Т при нормальном падении волн связаны с энергетическими коэффициентами r и t соотношениями: r = R², t = Т², эффективность защиты

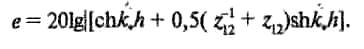
При распространении звука в атмосфере значение импеданса будет зависеть от температуры и давления. Значение z_* = 400 Па×с/м будут соответствовать условиям, когда, например, давление и температура будут соответственно равны 0,9×10⁵ Па (675 мм рт. ст.) и -27 °С или 1,013×10¹⁵ Па и +38,8 °С. Однако при изменении давления и температуры в пределах обычной атмосферы уровень импеданса L_z = 101gz/z_* незначителен и им пренебрегают, полагая, что

Lp(f̂) = L_I(f̂).

Уровень интенсивности или плотности потока энергии можно определить, используя зависимости (6.29), (6.30), (6.33).

Для расчета уровня шума в изолированном объеме используют уравнение (6.33), которое записывают в децибелах в виде

(6.43)

где — уровень плотности потока энергии на сферической поверхности радиуса r, образованной телесным углом излучения W при данном значении постоянной изолированного объема B=aS/(1 - a), где S— общая площадь его внутренней поверхности с коэффициентом поглощенияa; e_d — затухание звука [(см. пояснения к формуле (6.29)], которое в большинстве случаев можно принять равным нулю, S(r) = 4pr².

Таблица 6.8.