Разработка математической модели прерывистого шлифования

ЛАБОРАТОРНАЯ РАБОТА 7 Разработка и анализ математической моделипрерывистого шлифования

Цель работы: совершенствование навыков разработки математических моделей динамических систем станков, и реализация их в пакете VisSim на примере моделирования параметрических колебаний.

Разработка математической модели прерывистого шлифования

Моделирование динамической системы прерывистого шлифования рассматривается применительно к процессу круглого наружного врезного шлифования (КНВШ).

Прерывистое шлифование применяется для уменьшения нагрева шлифуемой поверхности за счет периодического прерывания его при прохождении заготовки через зону контакта. Для этого на периферии круга формы ПП выполняются пазы. Схема такого шлифования показана на рис. 7.1.

Рисунок 7.1 – Схема прерывистого шлифования
периферией круга формы ПП

При жесткой схеме шлифования круг подается на определенную глубину h _з механизмом подачи. При этом поверхность заготовки в пределах дуги контакта L будет шлифоваться, когда она контактирует с выступом круга длинной l ₁,и шлифование будет прерываться, отсутствовать, когда над дугой L будет паз длиной . Таким образом, важнейший параметр процесса шлифования – сила резания будет меняться. Меняться будут и упругие деформации упругой системы (УС) станка, а значит, возникнут параметрические колебания.

Представляет несомненный интерес знать, уметь определить параметры возникающих колебаний и, прежде всего, амплитуду или размах этих колебаний, в направлении перпендикулярном шлифуемой поверхности, что непосредственно отражается на геометрических параметрах прошлифованной поверхности, таких как шероховатость и волнистость.

При разработке графической схемы процесса шлифования сопротивление внедрению круга в шлифуемую поверхность представляют как сопротивление пружины жесткостью j, и в этом случае, модель процесса шлифования будет следующей:

, (7.1)

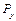где – глубина шлифования; – нормальная составляющая силы резания; j – жесткость процесса шлифования.

Жесткость процесса шлифования получают в результате линеаризации относительно экспериментальной зависимости силы 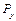от условий шлифования (режимов, характеристики круга, материала заготовки).

При прерывистом шлифовании сила 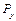, как отмечено выше, меняется, т.е. меняется жесткость процесса шлифования, как показано на рис. 7.2.

Рисунок 7.2 – Изменение жесткости процесса шлифования

Когда выступ круга длиной l ₁ полностью перекрывает дугу контакта L, то в течение времени жесткость процесса шлифования равна j, а когда полностью отсутствует контакт круга с заготовкой, т.е. в течение времени , . Таким образом, жесткость процесса шлифования периодически меняется от нуля до .

При построении графика учтено, что и время изменения от j до нуля и наоборот от нуля до равно .

Длина дуги контакта L при круглом шлифовании невелика. Особенно она мала при врезном шлифовании на чистовой поперечной подаче, т.е. с малой глубиной шлифования. Поэтому, в данном случае, время переходной фазы жесткости от j до нуля будет мало по сравнению с фазами и и, следовательно, переходной фазой можно пренебречь. Тогда модель изменения можно представить ступенчатым графиком, как показано на рис. 7.3 сплошной линией.

Рисунок 7.3 – Модель изменения : сплошная линия – при малой глубине шлифования; пунктирная линия – при большой глубине шлифования

Период Т ступенчатого сигнала найдем из выражения:

,

где n – число пазов в круге; – диаметр круга.

Соотношение между величинами выступа l ₁ и паза l ₂ на круге зададим через величину 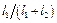, которую назовем скважностью по аналогии с этим понятием в импульсной технике как отношения продолжительности импульса к периоду между ними. Таким образом:

.

При шлифовании на черновой, т.е. большой скорости поперечной подачи V _поп, когда продолжительность переходной фазы составляет значительную долю от продолжительности фаз и , рационально представить зависимость в виде гармонической функции:

,

где , рад/с.

Этот сигнал показан на рис. 7.3 пунктирной линией.

Функциональная схема процесса прерывистого шлифования в замкнутой технологической системе определяется принятой дискретной моделью станка и обобщенными координатами, движение по которым описывает поведение системы в динамике. В настоящей работе рассматривается изменение глубины шлифования при достаточно высокочастотном воздействии прерывистой поверхностью круга. Поэтому в связи с большой инерционностью шлифовальной бабки (масса ее для станка 3М151 – 500 кг) она не будет реагировать на высокие частоты колебаний, возникающие в процессе резания. Поэтому можно ограничиться двухмассовой моделью станка, состоящей из приведенных масс заготовки и круга на шпинделе, установленного в неподвижной шлифовальной бабке.

Следовательно, графическую схему динамической системы КНВШ можно изобразить так, как показано на рис. 7.4:

Рисунок 7.4 – Графическая схема динамической системы КНВШ:
1-заготовка, 2-шлифовальный круг, 3-шпиндель, 4-шлифовальная бабка,
5-вкладыш гидродинамического подшипника

Заготовка 1 массой вращается со скоростью и ее соединение со станиной моделируемая пружиной жесткостью и демпфером с коэффициентом демпфирования . Шлифовальный круг 2 закреплен на шпинделе 3, который на гидродинамических подшипниках с вкладышами 5 установлен в корпусе шлифовальной бабки 4. Круг со шпинделем имеет массу и вращается со скоростью . Соединение шпинделя 3 с шлифовальной бабкой 4 моделируется пружиной жесткостью и демпфером с коэффициентом демпфирования . 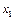Обобщенными координатами динамической системы ДС КНВШ являются перемещения и 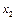соответственно заготовки и круга на шпинделе.

В соответствии со схемой на рисунке 7.4 можно графически изобразить функциональную схему замкнутой системы прерывистого КНВШ (см. рис. 7.5)

При рассмотрении связей между элементами ДС КНВШ принимаем как очевидный факт, что установившийся процесс прерывистого шлифования – это шлифование с какой-то средней глубиной и периодическими отклонениями от нее. Поэтому в какой-то момент времени входным сигналом в ДС КНВШ может быть это среднее значение глубины шлифования , и эта глубина задается настройкой станка, обеспечивающей среднее значение натягов пружин, соединяющих заготовку и круг со станиной (см. рис. 7.4), т.е. при среднем значении силы .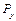

Рисунок 7.5 – Функциональная схема замкнутой
динамической системы прерывистого КНВШ

Прерывистость контакта круга с заготовкой вызывает отклонение натягов пружин от их средних значений.

Рассмотрим мгновение времени, когда натяг пружин увеличивается, т.е. растет сила 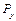, и соответственно растут деформации пружин, т.е. перемещения 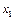и 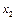. Общая суммарная их деформация .

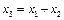При принятом направлении осе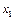й и 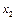круг и заготовка удаляются друг от друга и глубина шлифования уменьшается. Поэтому сигнал 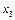по обратной отрицательной связи подается на сумматор, где он вычитается из – средней глубины шлифования.

В результате вычитания из 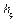на выходе сумматора формируется фактическая глубина шлифования – .

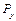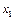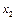Процесс шлифования преобразует в силу , которая, в свою очередь, перемещает круг и заготовку на и соответственно. Таким образом и функционирует замкнутая динамическая система прерывистого КНВШ.

Для моделирования ДС прерывистого КНВШ необходимо описать уравнениями все элементы этой ДС.

Процесс шлифования, как отмечено выше, моделируется выражением (7.1).

В качестве зависимости 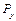от условий шлифования кругом со сплошной режущей поверхностью принята эмпирическая зависимость, полученная в станочной лаборатории Опытно-конструкторского бюро шлифовальных станков Харьковского станкостроительного завода [8].

Для условий: материал заготовки – сталь 40Х, круг 750х305х60 24А10СМ1К после правки алмазным карандашом с продольной подачей 150 мм/мин и глубиной 0,01 мм, полученная зависимость имеет следующий вид:

, Н (7.2)

где В – ширина шлифования, мм; – скорость поперечной (врезной) подачи, мм/мин; – скорость вращения заготовки, м/мин.

Для перехода к зависимости (7.1) выразим глубину шлифования через и при диаметре заготовки мм:

. (7.3)

Подставив из (7.3) значение в (7.2) получим:

, Н (7.4)

Для получения линейной зависимости (7.1) линеаризуем (7.4) относительно разложив (7.4) в ряд Тейлора и отбросив члены высшего порядка малости:

,

где – значение 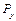при условиях шлифования в равновесном установившемся режиме; 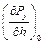– производная 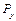по в равновесном режиме.

Подставив 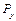из (7.4) получим:

Поскольку в динамике рассматривается отклонение силы резания от ее значения в установившемся режиме, то записываем полученное выражение, опуская знак :

Таким образом, сомножитель в (7.1) будет следующим:

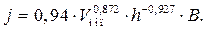(7.5)

Осталось описать уравнениями движение масс и в мгновение, когда сила 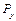растет от ее среднего значения, т.е. в мгновение, которое рассматривалось при формировании функциональной схемы. Направления и величины действующих сил на массы и показаны на рис. 7.6.

Рисунок 7.6 – Силы, действующие на массы и

Растущая сила 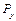перемещает массу . Этому перемещению противодействует усилие пружины и демпфирования . Все эти силы в динамике уравновешиваются силой инерции . Таким образом, уравнения равновесия сил на массе (заготовке) будет следующим:

.

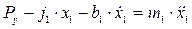По аналогии получаем равновесие сил на массе (шлифовальном круге):

.

При этом надо иметь в виду, что фактическое значение силы 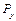получим согласно функциональной схеме (рис. 7.5) следующим:

где .

Таким образом, имеем следующую систему уравнений описывающих ДС прерывистого КНВШ:

(7.6)