Розрахункові завдання

1. В задачах 1.1 – 1.31 знайти суму ряду.

1.1	1.2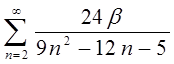
1.3	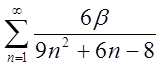1.4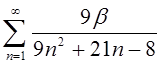
1.5	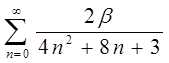1.6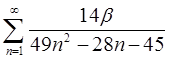
1.7	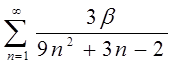1.8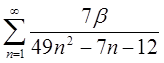
1.9	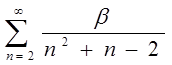1.10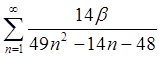
1.11	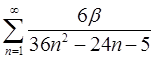1.12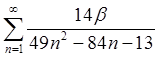
1.13	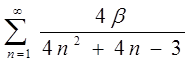1.14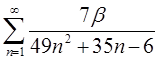
1.15	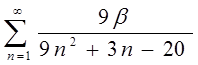1.16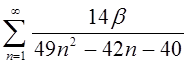
1.17	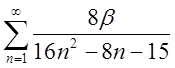1.18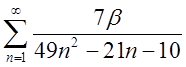
1.19	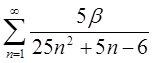1.20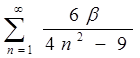
1.21	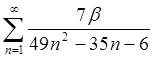1.22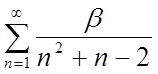
1.23	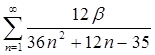1.24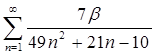
1.25	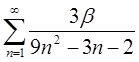1.26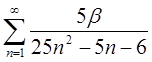
1.27	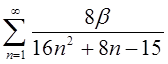1.28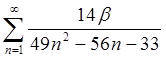
1.29	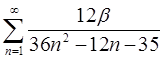1.30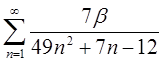
1.31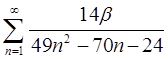

2. В задачах 1.1 – 1.31 дослідити ряд на збіжність за допомогою ознаки Даламбера

2.1	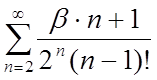2.2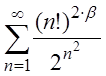
2.3	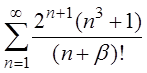2.4
2.5	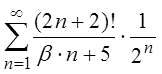2.6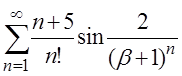
2.7	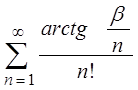2.8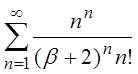
2.9	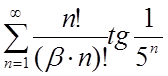2.10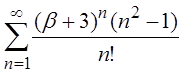
2.11	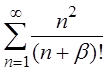2.12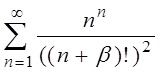
2.13	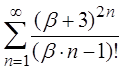2.14
2.15	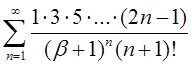2.16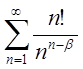
2.17	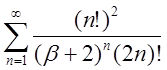2.18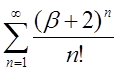
2.19	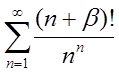2.20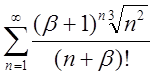
2.21	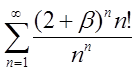2.22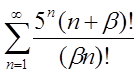
2.23	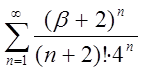2.24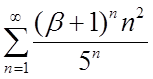
2.25	2.26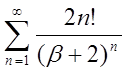
2.27	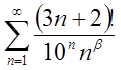2.28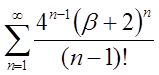
2.29	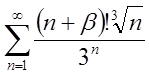2.30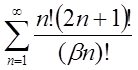
2.31

3. В задачах 3.1 – 3.31 дослідити ряд на збіжність за допомогою радикальної ознаки Коші.

3.1	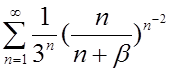3.2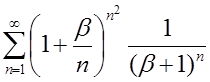
3.3	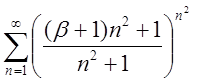3.4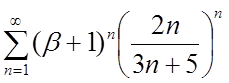
3.5	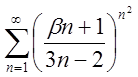3.6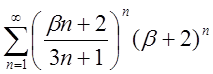
3.7	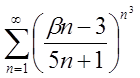3.8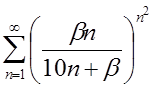
3.9	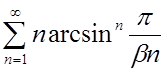3.10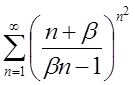
3.11	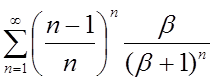3.12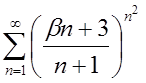
3.13	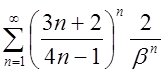3.14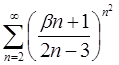
3.15	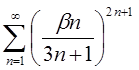3.16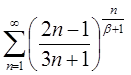
3.17	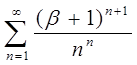3.18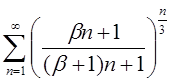
3.19	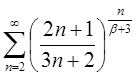3.20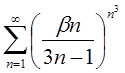
3.21	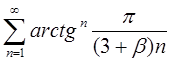3.22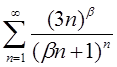
3.23	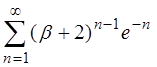3.24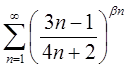
3.25	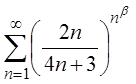3.26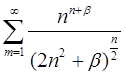
3.27	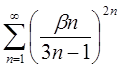3.28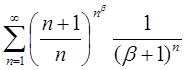
3.29	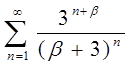3.30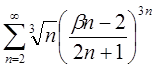
3.31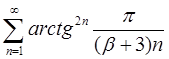

4. В задачах 4.1 – 4.31 дослідити ряд на збіжність за допомогою інтегральної ознаки Коші.

4.1	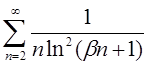4.2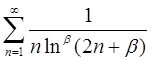
4.3	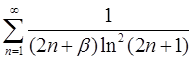4.4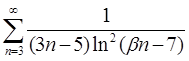
4.5	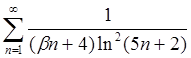4.6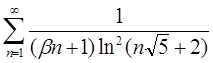
4.7	4.8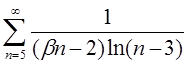
4.9	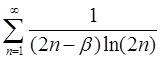4.10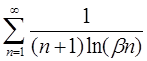
4.11	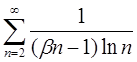4.12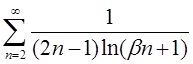
4.13	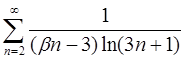4.14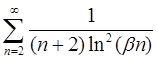
4.15	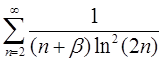4.16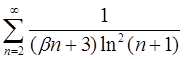
4.17	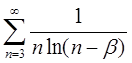4.18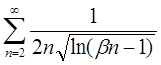
4.19	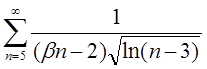4.20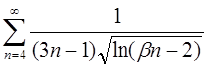
4.21	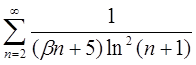4.22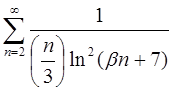
4.23	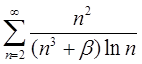4.24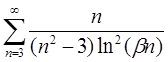
4.25	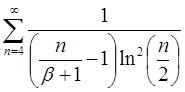4.26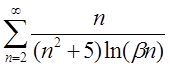
4.27	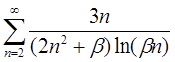4.28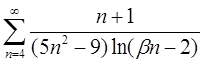
4.29	4.30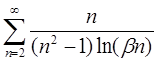
4.31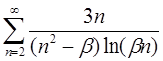

Методичні рекомендації.

Задача 1.31.

При 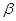=1 .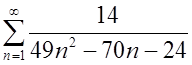

Розв’язання.

Сума ряду визначається за формулою 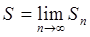, де 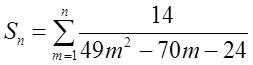. Розкладемо раціональний дріб на прості дроби. Знаменник дробу розкладемо на множники, для цього прирівняємо знаменник до нуля і розв’яжемо відповідне квадратне рівняння. Одержимо корені: 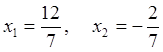. Отже, знаменник має вид 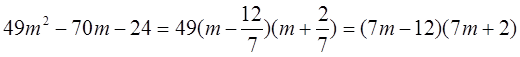. Методом невизначених коефіцієнтів представимо дріб в вигляді суми елементарних дробів першого типу: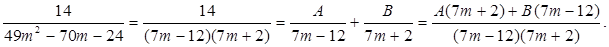

14=А(7m+2)+B(7m-12), при 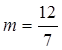маємо: 14=14A, отже A=1, а при маємо: 14= - 14B, отже B= - 1.

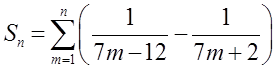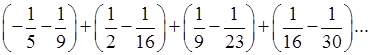
Таким чином = = 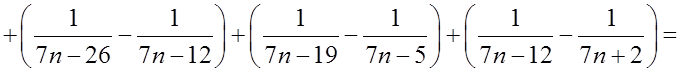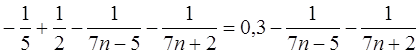, і сума ряду буде

дорівнювати .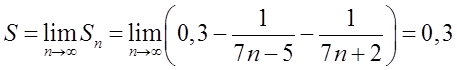

Задача 2.31.

При 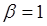необхідно дослідити на збіжність ряд

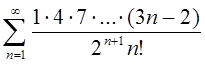
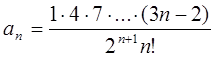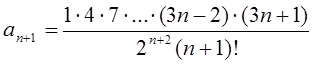Розв’язання: Для дослідження на збіжність ряду з додатними членами скористаємось ознакою Даламбера. В даному ряді , а та

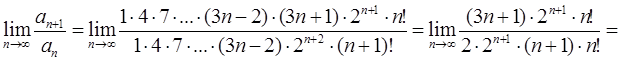
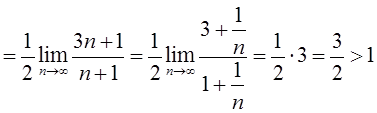. Отже за ознакою Даламбера даний ряд розбігається.

Задача 3.31.

При b=1 необхідно дослідити на збіжність ряд

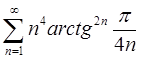
Розв’язання: Для дослідження даного ряду з додатними членами на збіжність скористаємось радикальною ознакою Коші. Маємо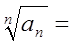

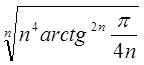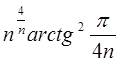= . Отже = .

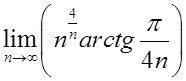Якщо 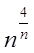представити як 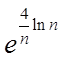, скориставшись неперервністю експоненти та застосувавши правило Лопіталя, будемо мати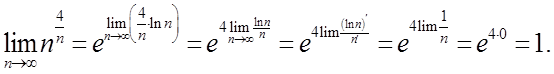

Скориставшись неперервністю степеневої та оберненої тригонометричної функцій, легко знаходимо, що 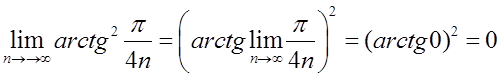. Таким чином, . Отже, за радикальною ознакою Коші, даний ряд розбігається.

Задача 4.31.

Приклад 1

При b=2 необхідно дослідити на збіжність ряд

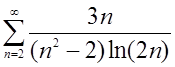
Розв’язання: Очевидно, що для всіх n=2,3,... має місце нерівність 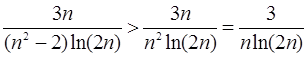. Розглянемо ряд 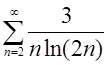(*) і дослідимо його на збіжність за допомогою інтегральної ознаки Коші. Розглянемо функцію 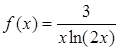, яка неперервна, приймає додатні значення і монотонно спадає на проміжку [2; 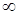) Обчислимо невласний інтеграл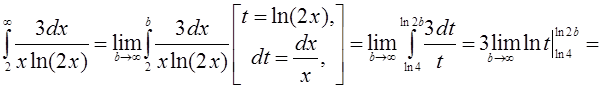

. Отже даний невласний інтеграл є розбіжним, а з цього випливає, що і ряд (*) також є розбіжним. А звідси випливає що за ознакою порівняння і даний ряд також є розбіжним.

Приклад 2

Дослідити на збіжність ряд .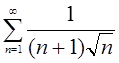

Розв’язання:

Оскільки 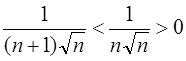розглянемо ряд 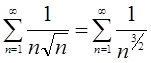(*). Дослідимо ряд (*) на збіжність за допомогою інтегральної ознаки Коші. Функція 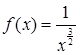неперервна, приймає додатні значення і монотонно спадає на проміжку [1; 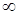). Знайдемо невласний інтеграл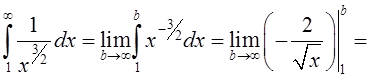 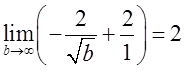. Невласний інтеграл збігається отже і ряд (*) також збігається, а з цього випливає, що за ознакою порівняння, і даний ряд також буде збігатися.

Список рекомендованої літератури

1. Пискунов Н. С. Дифферинциальное и интегральное исчисления для втузов. Т.2 / Н. С. Пискунов – М.: Наука, 1985. – 560с.

2. Барковський В. В. Вища математика для економістів / В. В. Барковський, Н. В. Барковська. – К.: ЦУЛ, 2002. – 400 с.

3. Вища математика: підручник / уклад. П. П.Овчинніков. – К.: Техніка, 2000.– 592с.

4. Соколенко О. І. Вища математика: підручник / О. І. Соколенко – К.: Академія, 2002. – 432с.

5. Берман Г. Н. Сборник задач по курсу математического анализа / Г. Н. Берман. – М.: Наука, 1985. – 383 с.

6. Дубовика В. П. Вища математика: збірник задач. / В. П. Дубовика, І. І. Юрина. – К.: 2001. – 480с.

7. Шкіль М. І. Математичний аналіз / М. І. Шкіль – К.: Вища школа, 1994. – 423с.

Зміст