Интерполяционный многочлен в форме Лагранжа

Будем искать интерполяционный многочлен в виде

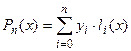, (1)

где 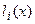- некоторые многочлены n -й степени. Подставим (1) в условие интерполяции:

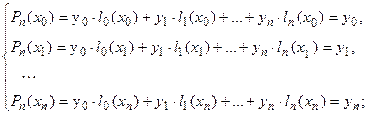(2)

Для выполнения условий интерполяции (2) достаточно выполнения следующих условий:

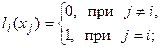(3)

.

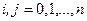Зафиксируем номер i и подберем многочлен 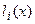так, чтобы выполнялись условия (3) при 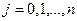. Из условия (4.1.8) следует, что корнями этого многочлена являются все узлы интерполяции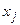 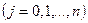, кроме одного узла - 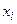. Следовательно, многочлен 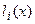можно представить в виде:

.

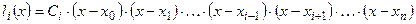Здесь 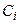- произвольная постоянная. Произведение, стоящее в правой части, можно записать более компактно с использованием символа произведения. Тогда последняя формула примет вид:

.

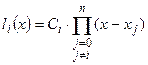Для определения неизвестной постоянной 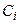воспользуемся последним оставшимся условием (3) при :

.

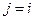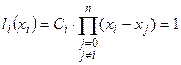Отсюда

,

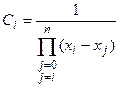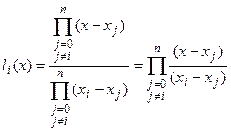
Подставим полученное представление для 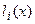в (1) и получим представление для интерполяционного многочлена:

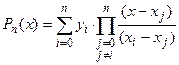(4)

Интерполяционный многочлен, записанный в виде (4) называют интерполяционным многочленом Лагранжа, а формулу (4) – интерполяционной формулой Лагранжа.