Постановка задачи интерполирования

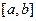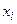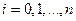Пусть функция определена на заданном отрезке . Известны значения этой функции в отдельных точках () этого отрезка. Вычисление значений этой функции в других точках 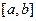либо очень трудоемко, либо вообще невозможно. В таких условиях обычно стараются получить приближение для функции , которым можно было бы воспользоваться, для вычисления приближенных значений функции в других точках отрезка 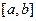или для других целей. Под приближением функции на 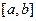понимается некоторая другая функция , определенная на 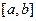, значения которой достаточно близки к соответствующим значениям функции .

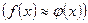При построении приближений для функций с известной таблицей значений используется несколько способов. Самый распространенный из них получил название интерполяции. При интерполяции от приближения требуется, чтобы оно имело ту же таблицу значений, что и приближаемая функция:

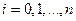, . (4.1.1)

Это условие получило название условия интерполяции. Функция , удовлетворяющая условиям интерполяции, называется интерполяционной, а точки - узлами интерполяции.

Чаще всего в качестве интерполяционных функций выбирают алгебраические многочлены, поскольку их значения проще всего вычисляются. В результате возникает следующая задача.

Задача многочленной интерполяции

Ищется алгебраический многочлен n -й степени , удовлетворяющий условиям интерполяции

(4.1.2)

Алгебраический многочлен, удовлетворяющий условиям (4.1.2), называется интерполяционным многочленом. При записи интерполяционного многочлена мы будем использовать также более развернутое обозначение , в котором указываются узлы интерполяции в качестве параметров.

Геометрический смысл интерполяции состоит в том, что графики функции и интерполяционного многочлена 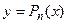должны проходить через все табличные точки , (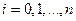). На рис. 4.1.1 эти точки выделены. Именно это условие должно обеспечить близость графиков этих функций на 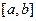, чтобы можно было использовать интерполяционный многочлен в качестве приближения для функции . Интуитивно понятно, что если табличных точек будет много и они будут расположены густо, то графики функции и интерполяционного многочлена 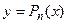будут расположены близко друг к другу.