 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
отображение вершин, входящих в это множество
|
|

Если множество S внутренне устойчиво, то для произвольной пары вершин из этого множества <xi, xj>, если і ≠ j, отображение S не должно пересекаться с S. Действительно, если вершина xi является отображением xj, или есть дуга, которая выходит из xi и входит в xj, то одна из вершин, xi или xj, не должна принадлежать S:
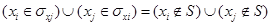 (1)
(1)
Это – формулировка внутренней устойчивости вершин графа.
Для того, чтобы произвольные вершины xk, xp принадлежали внутренне устойчивому множеству вершин графа S, должно выполняться:
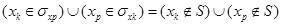 (2)
(2)
Возьмем конъюнкцию левых и правых частей выражений (1) и (2)

(3) 
Геометрический смысл выражения (3):
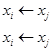
| 
| 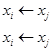
| 
| 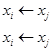
| 
| 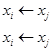
| = |
= 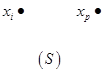
| 
| 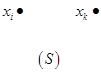
| 
| 
| 
| 
|
В выражении (3)перебираются всевозможные способы исключения вершин xi, xj, xk, xp из множества S так, чтобы оно было внутренне устойчивым.
Тогда можно составить следующий алгоритм:
Алгоритм поиска всех максимальных внутренне устойчивых множеств:
1. Для каждой пары (xi, xj) графа выписывается выражение (1).
2. Берется конъюнкция всех полученных выражений (для всех пар), раскрываются скобки, и производится поглощение ( ).
).
3. В полученной записи для каждой конъюнкции выписываются все вершины графа, которые в нее (конъюнкцию) не вошли. Они и образуют максимальные внутренне устойчивые множества вершин графа.
На практике выражение (1) используют в более формализованном виде:

Тогда выражение (1) будет иметь вид:

 Добавим конъюнкции слева и справа
Добавим конъюнкции слева и справа  . Получим:
. Получим:

Для всех вершин графа

Пример. Дана матрица смежности графа.
| R= | ||||||
Запишем выражение (1) для всех вершин графа (для всех пар):
 v
v  v
v  ∙
∙  =1 Þ
=1 Þ  v
v  =1
=1
 v
v 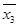 v
v  ∙
∙ 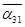 =1 Þ
=1 Þ  v
v 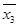 v 1=1 Þ 1≡1, т.е. эта строка нам далее не нужна
v 1=1 Þ 1≡1, т.е. эта строка нам далее не нужна
 v
v  v
v  ∙
∙  =1 Þ
=1 Þ  v
v  =1
=1
 v
v  v
v  ∙
∙  =1 Þ
=1 Þ  v
v  =1
=1
 v
v 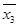 v
v  ∙
∙  =1 Þ
=1 Þ  v
v 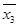 =1
=1
 v
v  v
v  ∙
∙  =1 Þ
=1 Þ  v
v  v 1=1 Þ 1≡1, т.е. эта строка нам далее не нужна
v 1=1 Þ 1≡1, т.е. эта строка нам далее не нужна
 v
v  v
v  ∙
∙  =1 Þ
=1 Þ  v
v  =1
=1
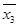 v
v  v
v  ∙
∙  =1 Þ
=1 Þ 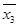 v
v  v 1=1 Þ 1≡1, т.е. эта строка нам далее не нужна
v 1=1 Þ 1≡1, т.е. эта строка нам далее не нужна
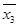 v
v  v
v  ∙
∙  =1 Þ
=1 Þ 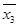 v
v  =1
=1
 v
v  v
v  ∙
∙  =1 Þ
=1 Þ  v
v  =1
=1
( v
v  )(
)( v
v  )(
)( v
v  )(
)( v
v 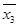 )(
)( v
v  )(
)(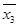 v
v  )(
)( v
v  ) = 1
) = 1
( v
v 

 )(
)( v
v 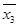
 )(
)( v
v 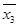
 ) = 1
) = 1
( v
v 

 )(
)(
 v
v 
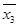
 v
v 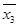
 v
v 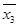

 ) =1
) =1


 v
v 

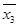
 v
v 
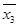
 v
v 
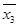

 v
v 

 v
v 
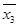

 =
=
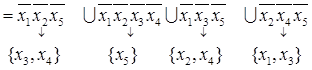

Процесс определения внутренне устойчивых множеств можно формализовать – вместо  будем пользоваться только индексом i
будем пользоваться только индексом i
Формальное использование метода Магу:
1. Взять i -ую строку матрицы смежности и записать для нее выражение
 , где
, где  ;
;
 соответствуют номерам столбцов матрицы, содержащим на пересечении со строкой i единицы.
соответствуют номерам столбцов матрицы, содержащим на пересечении со строкой i единицы.
2. Операцию (п.1) провести для всех строк.
3. Выполнить конъюнкцию полученных выражений и упростить.
4. В итоговом выражении для каждой конъюнкции выписать не вошедшие в нее индексы.
5. Сформировать соответствующие внутренне устойчивые множества и определить число внутренней устойчивости графа  .
.
ПРИМЕЧАНИЯ: А. Петли игнорируются!!!
Б. Пустые строки не учитываются!!!
Для этой же матрицы смежности (R)
( )
)


 Результат тот же
Результат тот же

Метод Магу определения числа внешней устойчивости графа.
Внешне устойчивое множество Т – это такое множество вершин графа G, что в каждую вершину xi графа, не принадлежащую Т, заходит дуга, исходящая из вершины множества Т:

Х – множество всех вершин графа.
Для всех вершин графа выполняется:

Другими словами, любая вершина xi либо принадлежит внешне устойчивому множеству Т, либо для нее всегда найдется вершина из множества Т, из которой исходит дуга, заходящая в данную вершину xi.
На основании выше изложенного запишем: 

Формула (1) показывает все возможные варианты положения вершины xi относительно внешне устойчивого множества Т.
Для вершины xk из множества Т:
(2) 
Выполним конъюнкцию левых и правых частей выражений (1) и (2):
(*) 

Таким образом, соотношение 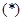 описывает все возможные способы распределения пары вершин xi и xk относительно внешне устойчивого множества Т, т.е. описывает процесс построения всех внешне устойчивых множеств при различных местоположениях вершин xi и xk.
описывает все возможные способы распределения пары вершин xi и xk относительно внешне устойчивого множества Т, т.е. описывает процесс построения всех внешне устойчивых множеств при различных местоположениях вершин xi и xk.
Соотношение (1) запишем более формально, приняв новые обозначения:
 ;
;
Значит,  ,
,


Получим
(1) 
В общем виде:  - основное соотношение.
- основное соотношение.
(* *) 
После раскрытия скобок в последнем выражении (* *) и проведения операции поглощения ( ) получим дизъюнкцию конъюнкций. В каждой конъюнкции перечисляются все вершины графа, образующие минимальные внешне устойчивые множества. Сколько конъюнкций, столько и множеств.
) получим дизъюнкцию конъюнкций. В каждой конъюнкции перечисляются все вершины графа, образующие минимальные внешне устойчивые множества. Сколько конъюнкций, столько и множеств.
Пример: Дана матрица смежности графа
| R= | ||||||
 x1 v x1 α11 v x2 α21 v x3 α31 v x4 α41 v x5 α51 = 1
x1 v x1 α11 v x2 α21 v x3 α31 v x4 α41 v x5 α51 = 1
x2 v x1 α12 v x2 α22 v x3 α32 v x4 α42 v x5 α52 = 1
x3 v x1 α13 v x2 α23 v x3 α33 v x4 α43 v x5 α53 = 1
x4 v x1 α14 v x2 α24 v x3 α34 v x4 α44 v x5 α54 = 1
x5 v x1 α15 v x2 α25 v x3 α35 v x4 α45 v x5 α55 = 1
| Выпишем все αij: | α11 = 0; α11 = 1; α13 = 0; α14 = 1; α15 = 1; |
| α21 = 0; α22 = 0; α23 = 1; α24 = 0; α25 = 0; | |
| α31 = 0; α32 = 1; α33 = 0; α34 = 0; α35 = 1; | |
| α41 = 0; α42 = 0; α43 = 0; α44 = 0; α45 = 0; | |
| α51 = 0; α52 = 1; α53 = 0; α54 = 1; α55 = 0; |
Перемножаем и выписываем в строку (конъюнкция):
| x1 = 1 | |
| x2 v x1 v x3 v x5 = 1 | x2 v x3 v x5 = 1 |
| x3 v x2 = 1 | |
| x1 v x4 v x5 = 1 | |
| x5 v x1 v x3 = 1 | x1 v x5 v x3 = 1 |
x1 (x2 v x3 v x5)(x3 v x2)(x1 v x4 v x5)(x1 v x3 v x5) = 1
(x2 v x3)(x2 v x3 v x5)(x1 v x3 v x5)(x1 v x4 v x5) = 1
(x2 v x2x3 v x2x5 v x3 v x3x5)(x1 v x1x4 v  x1x5 v x1x3 v x3x4 v x3x5 v x1x5 v x5x4 v
x1x5 v x1x3 v x3x4 v x3x5 v x1x5 v x5x4 v
v x5) = 1
(x2 v x3 v x2x5)(x1 v x5 v x1x4 v x1x3 v x3x4 v x3x5)(x2 v x3)(x1 v x5 v x3x4) = 1
x1x2 v x2x5 v x2x3x4 v x1x3 v x3x5 v x3x4 = 1
x1x2 v x2x5 v x3x4 v x1x3 v x3x5 = 1
x1x2 v x1x2x5 v  v x1x3 = 1
v x1x3 = 1
Формальное использование метода Магу.
1. Для j-го столбца матрицы смежности записать выражение вида:
 , i, j, k, l,…p – строки матрицы смежности, дающие на пересечении со столбцом j число 1.
, i, j, k, l,…p – строки матрицы смежности, дающие на пересечении со столбцом j число 1.
2. Выполнить п.1 для всех столбцов матрицы смежности.
3. Взять произведение всех полученных выражений и упростить его, раскрывая скобки и выполняя операцию поглощения.
4. В полученном выражении каждая конъюнкция определяет внешне устойчивое множество.
5. Среди полученных внешне устойчивых множеств выбираем минимальное для определения  .
.
1 (2 v 1 v 3 v 5)(3 v 2)(4 v 1 v 5)(5 v 1 v 3) =
= (23 v 2 v 13 v 12 v 3 v 32 v 53 v 52)(45 v 41 v 43 v 15 v 1 v 13 v 5 v  v 53) =
v 53) =
= (3 v 2)(1 v 5 v 43) = 31 v 35 v 43 v 12 v 25 v 234 =
= 31 v 35 v 43 v 12 v 25 = 31 v 135 v 12 v 125 v 143 =
= 13 v 135 v 12 v 125 v 143 = 13 v 12 v 143
Определяем ядро графа:
{ 3,4} ∩ { 3, 4} = {3,4}
Метод Магу определения хроматического числа.
Разбиваем граф на внутренне устойчивые взаимно непересекающиеся множества.
Алгоритм определения хроматического числа графа:
1. В формуле (1) метода Магу для поиска внутренне устойчивых множеств раскрываем скобки, упрощаем выражение. Получим дизъюнкцию конъюнкции некоторых выражений 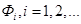 , содержащих все вершины графа, которые не входят в максимальное внутренне устойчивое множество ρi
, содержащих все вершины графа, которые не входят в максимальное внутренне устойчивое множество ρi
(2) 
2. Каждому Фi из (2) поставить в соответствие булеву переменную yi, такую, что 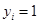 только на вершинах max внутренне устойчивого множества ρi, и
только на вершинах max внутренне устойчивого множества ρi, и  для остальных вершин.
для остальных вершин.
3. Для каждой вершины xi графа найти все элементы  , в которые вершина xi не входит, и записать выражение
, в которые вершина xi не входит, и записать выражение
(3) 
Записать выражение (3) для всех вершин графа.
4. Взять конъюнкцию всех полученных выражений. Раскрыть скобки и произвести все упрощения.
Получим выражение вида:
(4) 
5. В выражении (4) найти такой член Ψi, который содержит минимальное количество букв:

и произвести раскраску max внутренне устойчивых множеств
Sm1, Sm2 … Smp следующим образом:
вершины множества Sm1 - в цвет 0;
за исключением общих Sm2 - в цвет 1;
за исключением общих Sm3 - в цвет 2
и т. д.
Хроматическое число γ равно числу переменных в конъюнкции Ψi.

| ||||||||
По методу Магу:


| Вершина 1 не входит в Ф1, Ф7 |

| Вершина 2 не входит в Ф5, Ф6, Ф8 |
| … | |
| … | |

| … |
Записываем это в виде:

| 1 Ï Ф1, Ф7 |
| 2 Ï Ф5, Ф6, Ф8 | |
| 3 Ï Ф1, Ф2, Ф3, Ф4, Ф7 | |
| Вершины | 4 Ï Ф1, Ф4 |
| 5 Ï Ф2, Ф3, Ф5, Ф6 | |
| 6 Ï Ф4, Ф8 | |
| 7 Ï Ф1, Ф3, Ф6 | |
| 8 Ï Ф2, Ф5, Ф7 |
Запишем выражение (3) для вершины x1, x2, x3,…., x8 (т.е. для 1, 2, 3,….8) и возьмем конъюнкцию:
(y1 v y7)(y5 v y6 v y8)(y1 v y2 v y3 v y4 v y7)(y1 v y4)(y2 v y3 v y5 v y6)(y4 v y8)(y1 v v y3 v y6)(y2 v y5 v y7) = 1
Раскроем скобки и упростим:
Ψ = y1y2y8 v y1y4y5 v y1y2y8 v y4y6y7 v y1y2y4y6 v y1y3y7y8 v y1y6y7y8 v y3y4y5y7 v
v y3y4y7y8
Хроматическое число 


| Ф1 = 2568 | Ф2 = 12467 | Ф8 = 134578 |
| ↓ | ↓ | ↓ |
| S1 = {1,3,4,7} | S2 = {3,5,8} | S8 = {2,6} |
↓
| В цвет «0» | S1 = {1,3,4,7} |
| В цвет «1» | S2 \ S1 = {5,8} |
| В цвет «2» | S8 \ (S2 \ S1) = {2,6} |
Дата публикования: 2015-07-22; Прочитано: 1304 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
