Экстремальные свойства выпуклых функций

1. Еслиf(x) выпуклая функция на выпуклом множестве X, то всякая точка локального минимума является точкой ее глобального минимума на X.

2. Если выпуклая функция достигает своего минимума в двух различных точках, то она достигает минимума во всех точках отрезка, соединяющего эти две точки.

3. Если f(x) строго выпуклая функция на выпуклом множестве X, то она может достигать своего глобального минимума на X не более чем в одной точке.

Определение 1.11. Функция f(x) удовлетворяет условию Липшица на отрезке [ а, в ], если существует такое число L > 0 (константа Липшица), что

для всех х' и х", принадлежащих [а,в]

5. Аналитические методы оптимизации

Наиболее просты с математической точки зрения случаи, когда целевая функция задается явной формулой и является при этом дифференцируемой функцией. В этом случае для поиска точек экстремума может быть использована производная.

Замечания:

1. Если требуется определить глобальные экстремумы, то они находятся в результате сравнения значений функции в точках локальных минимумов и максимумов с учетом ограниченности функции на .

2. Для случая функции f (х) одной переменной (n = 1) можно сформулировать правило:Если функция f(x) и ее производные непрерывны, то точка х* является точкой экстремума тогда и только тогда, когда число т - четное, где т – - порядок первой не обращающейся в нуль в точке х* производной. Если то в точке х* - локальный минимум, а если то в точке х* - локальный максимум. Если число т нечетное, в точке х* нет экстремума.

Функция f(x) имеет локальный минимум в точке х₀, если существует некоторая положительная величина d (дельта) такая, что если , то .

Функция f(x) имеет глобальный минимум в точке х^*, если для всех х справедливо неравенство: f(x)³ f(х^*)

Пример. Определить экстремумы функции, представленной на рис. 3.1

x₀ х^*

x_m x_c x

Рис. 3.1.

Мы должны найти значения х₀ и х^*, т.е. найти уравнения, которые должны удовлетворять. Наша функция 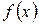непрерывная, ее производные тоже непрерывные, и в точках х₀ и х^* производная равна 0. .Следовательно, уравнение является только необходимым условием существования min, но не достаточным.

Т.к. в точке минимума первая производная является возрастающей функцией, а степень возрастания определяется знаком второй производной, поэтому по знаку второй производной можно определить тип экстремума:

и в этих точках существует минимум функции.

А вторая производная в точке максимума меньше нуля.

6. Метод множителей Лагранжа

С помощью метода множителей Лагранжа можно определить экстремальные точки функции многих переменных при наличии дополнительных связей между оптимизируемыми параметрами. Это один из методов для решения экстремальных задач с ограничениями в виде равенств, который сводит задачу с ограничениями к обычной экстремальной задаче без ограничений, которая решается известными способами.

Функция называется функцией Лагранжа, а числа - множителями Лагранжа. Необходимые условия экстремума функции состоят в равенстве нулю всех первых частных производных от по .

1. Составляют функцию Лагранжа.

2. Вычисляют частные первые производные от функции Лагранжа по переменным 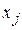и и приравнивают их нулю.

3. Решая, систему уравнений (3.4), определяют точки, в которых целевая функция (3.1) может иметь экстремум.

4. Среди точек, подозрительных на экстремум, находят такие, в которых достигается экстремум (минимум или максимум), и вычисляют значения целевой функции (3.2) в этих точках.

5. По знаку второй производной от функции Лагранжа 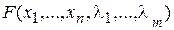по переменным 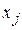определяют тип экстремума.

Для решения экстремальных задач с ограничениями в виде равенств используется метод множителей Лагранжа, сводящие задачу с ограничениями к обычной экстремальной задачи без ограничений.

7. Задачи нелинейного программирования. Численные методы решения безусловной минимизации одномерных функций.(метод сканирования)

Наиболее простым способом сужения интервала неопределенности является деление его на некоторое число равных частей с последующим вычислением значения целевой функции в точках разбиения.

у(х) - Здесь функция унимодальна в интервале - шаг

а в х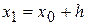

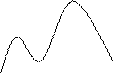
у(х) - функция не унимодальна

а в х

Пусть n – число элементарных отрезков, на которые мы разделим интервал неопределенности . Координаты точек разбиения вычисляются по формуле . Вычисляем значения целевой функции в точках разбиения. Сравнивая полученные значения

, найдем среди них экстремальное (наименьшее или наибольшее). Число можно приближенно принять за наименьшее значение целевой функции на интервале . Очевидно, что близость к минимуму зависит от числа точек разбиения и для непрерывной функции

,

т.е. с увеличением числа точек разбиения погрешность в определении минимума стремится к нулю.

Уменьшение начального интервала в этом методе определяется по формуле:

, где n – количество вычислений функции.

8. Задачи нелинейного программирования. Численные методы решения безусловной минимизации одномерных функций.(метод дихотомии)

Его идея заключается в следующем:

делим интервал неопределенности пополам и размещаем две точки и симметрично середины отрезка на расстояниях , т.е.

а в

х₁ С х₂

В данном случае пусть мы ищем минимум целевой функции и знаем, что функция унимодальна. В этих точках и вычисляем значения целевой функции:

При сравнении значений получили, что . Тогда становится возможным указать новый интервал неопределенности. Точка с меньшим значением функции () указывает ту часть интервала, которую надо взять для дальнейшего рассмотрения. Из дальнейшего рассмотрения исключаем интервал .

а в

х₃ С х₄

Получив, таким образом новый интервал неопределенности (), можно повторно применить к нему всю описанную процедуру, используя для этого вторую пару точек и . Вычисляем в этих точках значения целевой функции:

Сранивая, получим .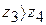

Т. к. 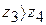и зная, что функция унимодальна и мы ищем минимум, можем исключить из дальнейшего рассмотрения отрезок интервала .

Процесс сужения продолжается до тех пор, пока конечная длина интервала не станет меньше заданной точности .

Если начальная длина интервала неопределенности равна единице

То после первого шага длина станет равной:

, затем

,

а после n вычислений:

9. Задачи нелинейного программирования. Численные методы решения безусловной минимизации одномерных функций.(золотого сечения)

В этом методе интервал неопределенности делится не на целое число частей, а в определенном иррациональном отношении. Суть этого метода состоит в следующем: интервал неопределенности делится на 2 неравные части, так что отношение длины всего интервала к длине большего отрезка равно отношению длины большего отрезка к длине меньшего отрезка. Деление отрезка в таком соотношении носит название «золотого сечения».

Длины последовательных интервалов берутся в фиксированном отношении:

– отношение «золотого сечения»;

так, чтобы и на k+1-ом шаге относительное расположение точек было тоже, что и на k-ом шаге.

Знаем, что функция унимодальная и мы ищем минимум функции.

х₂х₁

0 1

Точку выбираем симметрично относительно точки , т.е. на тех же расстояниях только и от других границ.

Прежде чем поставить мы должны вычислить значение целевой функции в точке и . Возможны 2 случая:

0 1

х₂ х₁ х ₃

1) функция унимодальна, ищем min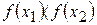

отбрасываем . Будем рассматривать

0 Х 1

х ₃ х₂

х₁

L

2)

отбрасываем , будем рассматривать интервал . Функция унимодальна, ищем минимум. Этот процесс будет продолжаться до тех пор, пока интеграл не будет меньше заданной точности.

(4.1)

(4.2)

(4.3)

Расписываем 3-е равенство следующим образом: в числитель подставляем вместо его значение из (4.2)

- длина интервала после - шагов.

В методе золотого сечения одно из значений целевой функции уже известно (это 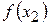или 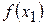), поэтому, начиная, с 3-го шага требуется вычислить только одно новое значение целевой функции в точке и т.д., определяемое правилом золотого сечения.

10. Задачи нелинейного программирования. Численные методы решения безусловной минимизации одномерных функций.(метод Фибоначчи)

В силу того, что в асимптотике , метод золотого сечения может быть трансформирован в так называемый метод чисел Фибоначчи. Однако при этом в силу свойств чисел Фибоначчи количество итераций строго ограничено. Это удобно, если сразу задано количество возможных обращений к функции.