Последовательность выполнения работы. 1. На поле чертежа наносят точки А, В, с плоскости р и точки D, Е, f плоскости q

1. На поле чертежа наносят точки А, В, С плоскости Р и точки D, Е, F плоскости Q. Координаты точек определяются в соответствии с индивидуальным вариантом задания по таблице в приложении 3.1.

2. Используя отмеченные на чертеже точки, изображают крылья складки Р и Q парными горизонталями с высотой сечения 200 м. При этом необходимо соответствие уровней горизонталей плоскостей (рис. 3.3), поскольку точки пересечения горизонталей одного уровня определят линию пересечения а (М₁₀₀₀, N₈₀₀) плоскостей Р и Q, т.е. ребро двугранного угла или шарнир складки.

Рис. 3.3

3. Грани Р и Q двугранного угла рассекают плоскостью Λ перпендикулярно к ребру а в точке Ν₈₀₀: l ^Λ = 1 /l ^а (рис. 3.4). Плоскость Λ пересекает плоскости Р и Q по линиям c и d: S ∩ Р = с (К₁₀₀₀, Ν₈₀₀), Λ ∩ Q = d (L₁₀₀₀, Ν₈₀₀). Угол между прямыми с и d является линейным углом α заданной складки (рис. 3.5).

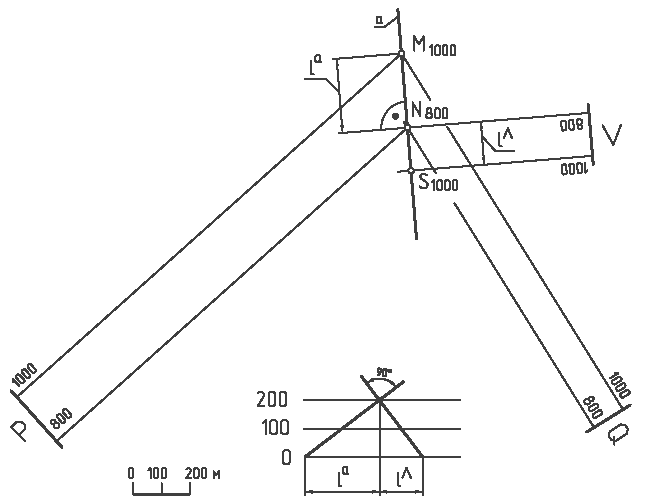
Рис. 3.4

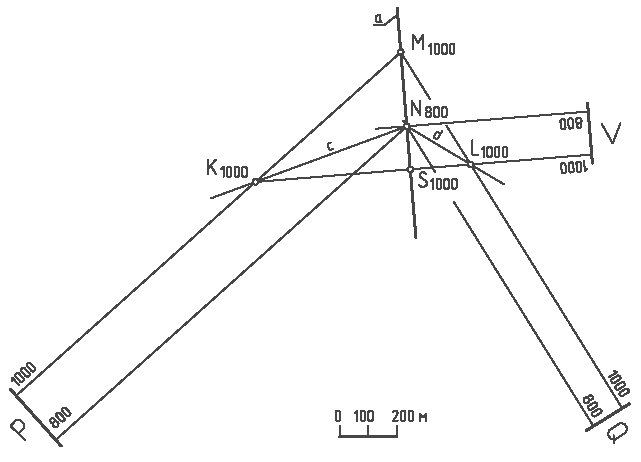
Рис. 3.5

4. Вращая плоскость линейного угла (с ∩ d) вокруг горизонтали h₁₀₀₀ (К₁₀₀₀, L₁₀₀₀), определяют его истинную величину (Ð L ₁₀₀₀), после чего вычерчивают биссектрису этого угла (рис. 3.6), сначала в совмещенном положении – (, Т₁₀₀₀), а затем в исходном – b (Ν₈₀₀, Т₁₀₀₀). Особенности преобразования чертежа методом вращения вокруг горизонтали подробно рассмотрены на рис. 3.2.

5. Через ребро а и биссектрису b отстраивают искомую биссекторную плоскость R заданного двугранного угла (рис. 3.6).

Рис. 3.6

6. Элементы залегания биссекторной плоскости определяются в любой ее точке, например в точке M₁₀₀₀ (рис. 3.7).

Рис. 3.7

Образец оформления работы 3 приведен в приложении 3.2.

Приложение 3.1