Основные положения и цель работы

При решении различного рода геологических задач может возникать необходимость позиционировать относительно частей света и горизонта изображенный на плане пласт породы. Обычно пласт имеет сложную форму, поэтому его поверхность делят на отдельные, условно плоские участки. Ориентирование каждой плоскости пласта производится путем определения элементов ее залегания – направления простирания, азимута и угла падения.

Положение плоскости в пространстве и ее изображение на чертеже вполне определяются одним из пяти известных из элементарной геометрии способов (рис. 2.1):

а) тремя точками, не лежащими на одной прямой, – θ (А, В, С);

б) прямой и точкой, не лежащей на этой прямой, – S (а, А; А Ë а);

в) двумя пересекающимися прямыми – Ψ (m ∩ n);

г) двумя параллельными прямыми – Φ (с || d);

д) любой плоской фигурой – W (АВС).

Рис. 2.1

На плане плоскость наиболее наглядно изображается проекциями ее горизонталей, представляющими собой параллельные прямые. Рассмотрим на конкретных примерах способы построения плоскости на плане.

Пример 1. Плоская кровля пласта S задана на плане тремя точками А, В и С (рис.2.2). Требуется изобразить горизонтали плоскости S.

Рис. 2.2

На плане определяют положение двух точек плоскости S с одинаковыми высотными отметками. Для этого интерполируют заложение АС (А – самая высокая из заданных точек плоскости,а С – самая низкая), определяя точку D, высотная отметка которой равна отметке заданной точки В. Прямая ВD является горизонталью h₁₀ плоскости S. Другие горизонтали плоскости S (h₂₀, h₃₀ и др.) проводят параллельно h₁₀ (рис. 2.3).

Рис. 2.3

Пример 2. Плоская кровля пласта S задана на плане точкой А₃₀ и направлением m (рис. 2.4). Требуется изобразить горизонтали плоскости S.

Рис. 2.4

На горизонтальной проекции прямой m с помощью интервала l^m, полученного на профильном изображении прямой (рис. 2.5), определяют точку С с отметкой 30 м.Прямая, соединяющая точку С с заданной точкой А, представляет собой горизонталь h₃₀ плоскости S. Остальные горизонтали плоскости проводят параллельно линии h₃₀.

Рис. 2.5

Пример 3. Плоская кровля пласта S задана на плане двумя направлениями m и n. Требуется изобразить горизонтали плоскости S.

Прямые m и n градуируют способом, показанным в примере 2. Через точки с одинаковыми высотными отметками проводят горизонтали плоскости S.

Простирание плоскости на плане определяется положением ее горизонталей. За направление простирания плоскости принято считать направление ее горизонталей в правую сторону, если стоять лицом к подъему (восстанию) плоскости (рис. 2.6).

Рис. 2.6

Азимутом простирания плоскости называется правый угол α, составленный северным направлением меридиана и направлением линии ее простирания (рис. 2.7).

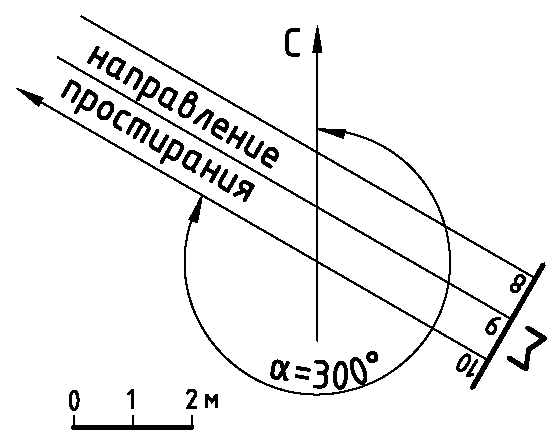
Рис. 2.7

Прямая u, лежащая в некоторой плоскости S и перпендикулярная к ее горизонталям, называется линией падения (или линией ската) плоскости (рис. 2.8). Интервал линии падения равен интервалу плоскости, в которой лежит эта линия: l ^u = l ^S. Соответственно, угол падения δ плоскости S равен углу, образованному линией ската u и ее горизонтальной проекцией: δ^S =δ ^u.

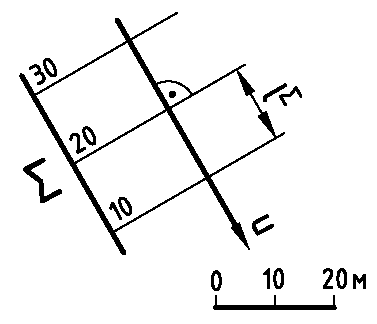
Рис. 2.8

Натуральную величину угла падения δ плоскости определяют на профильном изображении линии ската u этой плоскости (рис. 2.9).

Рис. 2.9

Направление падения линии u определяет направление падения плоскости S. Азимутом падения плоскости называется правый угол β, образованный северным направлением меридиана и направлением падения линии ската u плоскости (рис. 2.10).

Рис. 2.10

Линии простирания и падения плоскости взаимно перпендикулярны, поэтому разница между азимутом падения и азимутом простирания плоскости составляет 90^о: (a = β – 90^о).

Мощностью пласта горных пород называют расстояние от плоскости кровли S до плоскости почвы Λ пласта (рис. 2.11). Различают видимую мощность m_вид, мощность по скважине m_скв, вертикальную m_верт и горизонтальную m_г мощность, нормальную или истинную мощность m_н.

Рис. 2.11

Пример 4. Определить нормальную мощность m_н пласта, кровля и почва которого заданы на плане двумя параллельными плоскостями Σ иΛ (рис. 2.12).

Нормальная мощность m_н пласта определяется кратчайшим расстоянием от его кровли до почвы. Для определения величины m_н выполняют вертикальный разрез вкрест простирания горизонталей плоскостей Σ иΛ. Вертикальная плоскость, проведенная по направлению линии ската плоскостей Σ иΛ, пересекает кровлю по линии АВ, а почву по линии CD. Кратчайшее расстояние EF = m_н между этими линиями определяют на профильном изображении.

Рис. 2.12

С помощью вспомогательных разрезов можно определять горизонтальную и вертикальную мощность пласта, мощность по скважине и т.п.

Целью работы «Элементы залегания горных пород» является:

– построение на плане геометрической модели пласта горных пород;

– ознакомление с методами решения позиционных и метрических задач на полученной геометрической модели.

СОДЕРЖАНИЕ РАБОТЫ

Исходные данные к работе «Элементы залегания горных пород», приведенные в приложении 2.1, содержат следующую информацию:

– кровля Σ и почва Λ пласта горных пород представлены параллельными плоскостями;

– кровля Σ определена на плане тремя точками, точкой и прямой (направлением) или двумя прямыми в зависимости от варианта задания, причем координаты точки А кровли заданы во всех вариантах;

– в вариантах 1, 2, 3, 4, 7, 8, 13 индивидуального задания известна истинная мощность m_н пласта горных пород, а в вариантах 5, 6, 9, 10, 11, 12 – одна из точек почвы Λ пласта;

– заданы координаты устья D наклонной скважины, вскрывающей кровлю Σ в точке Е под прямым углом.

При выполнении работы учащийся решает следующие основные задачи:

– вычерчивает на плане горизонтали кровли Σ и почвы Λ пласта горных пород и определяет элементы залегания кровли;

– строит профильное изображение пласта и измеряет наклонную глубину скважины DЕ и ее зенитный угол γ (рис. 2.13);

Рис. 2.13

– определяет конечное положение Е забоя скважины на плане;

– измеряет нормальную (истинную) мощность m_н пласта (в вариантах 5, 6, 9, 10, 11, 12).