Пассивные сглаживающие фильтры

Их сглаживающее действие основано на накоплении энергии в реактивных элементах от сети в моменты её максимума и передачи в нагрузку в моменты её минимума. Основные схемы пассивных фильтров приведены на рис.3.25.

Рисунок 3.25 – Схемы пассивных сглаживающих фильтров

В резонансных фильтрах контур L_к C_к настраивается на частоту той гармоники, которую следует подавить. Обычно это первая гармоника. В компенсированном фильтре дроссель кроме основной обмотки имеет ещё небольшую компенсационную обмотку W_к. Переменные составляющие напряжения, обусловленные током i _~ на индуктивности и ёмкости противофазны и, в выходном напряжении, компенсируют друг друга. Это позволяет снизить пульсации в 3…5 раз, но требуется настройка и не должно быть перекомпенсации. Фильтр хорошо работает при неизменной нагрузке. В системах

с высокочастотными составляющими пульсаций применяют многозвенные фильтры (рис. 3.26). Каждое звено имеет свою полосу пропускания: по частоте сети, по частоте преобразования и помехам.

Рисунок 3.26 – Многозвенный фильтр для импульсных выпрямителей

Здесь С1- электролитический конденсатор большой ёмкости, С2 - плёночный, С3 - керамический конденсатор; 1 и 2 кабельные индуктивности – ферритовые кольца, нанизанные на проводники (они не имеют межвитковой ёмкости и не пропускают крутые фронты импульсных помех).

Сглаживающий фильтр характеризуется коэффициентом сглаживания пульсаций, под которым понимают отношение коэффициента пульсаций на входе к коэффициенту пульсаций на выходе фильтра [3]:

(3.23)

Отношение постоянной составляющей на выходе к постоянной составляющей на входе называют КПД фильтра, тогда

, (3.24)

где – КПД фильтра.

В общем случае, сглаживающий фильтр является частотно зависимым делителем напряжения Z₁ и Z₂, как показано на рис.3.26.

Рисунок 3.27 – Схема замещения фильтра для первой гармоники

Наибольшие трудности для сглаживания представляет именно первая гармоника пульсаций. Для неё получим: 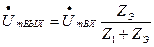, где . Отсюда находим

(3.25)

Подставив (3.25) в (3.24), нетрудно получить

(3.26)

Выражение (3.26) справедливо для пассивных ФНЧ и показывает, что чем больше Z₁ и меньше Z₂, тем выше коэффициент сглаживания.

L – фильтр. Возьмём простейший индуктивный фильтр и найдём модуль его коэффициента сглаживания. Очевидно, что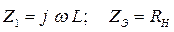

, (3.27)

где под КПД понимается отношение , а величина r_L– омическое сопротивление дросселя. Зависимость q от тока нагрузки показана на рис.3.28.

Рисунок 3.28 – Зависимость коэффициента сглаживания от тока нагрузки

для L – фильтра

С уменьшением тока (R_Н возрастает) КПД стремится к 1. При увеличении тока (R_Н уменьшается) q согласно выражению (3.27) растёт. Очевидно, что дроссель должен быть линейным (индуктивность не зависит от тока нагрузки) для чего требуется немагнитный зазор в магнитопроводе. Величина индуктивности дросселя такова, что дроссель полностью не разряжается за период пульсаций, то есть ток дросселя не спадает до нуля.

Значит, индуктивность должна быть больше некоторой критической величины . Таким условием является следующее неравенство

, (3.28)

где ; ; ;

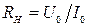
После подстановки получим

(3.29)

Рассчитывая на худший случай, в формулу следует подставлять минимальный ток нагрузки и если , то . Поэтому индуктивные фильтры целесообразны при больших токах нагрузки.

LC-фильтр (Г-образный). Здесь КПД определяется, как и в предыдущей схеме, а сопротивление (3.30)

Поскольку сопротивление конденсатора первой гармонике тока много меньше сопротивления нагрузки 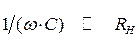, то .

Тогда . (3.31)

Здесь важным является – отсутствие резонансных явлений на частотах близких к частоте первой гармоники пульсаций, а входное сопротивление фильтра должно иметь индуктивный характер. Обычно это выполняется при q >3 и собственной частоте фильтра

(3.32)

При протекании тока I₀ через сглаживающие фильтры с индуктивностями, в последних накапливается энергия

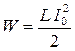(3.33)

При коммутации или обрыве нагрузки эта энергия освобождается – возникает ЭДС самоиндукции, которая поддерживает падающий ток

(3.34)

Величина этой ЭДС может превышать номинальное напряжение выпрямителя на десятки и сотни процентов. Перенапряжение зависит от перепада тока () и волнового сопротивления фильтра

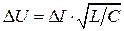(3.35)

Характер переходного процесса может быть колебательным или апериодическим. Вышесказанное иллюстрируется эпюрами рис.3.29.

Рисунок 3.29 – Напряжение на выходе фильтра при изменении

сопротивления нагрузки

С – фильтр. Возьмём простейший ёмкостный фильтр и найдём его коэффициент сглаживания. Здесь напряжения на входе и выходе одинаковы, поэтому следует говорить о модуле коэффициента передачи переменной составляющей тока от источника в нагрузку. Эквивалентная схема показана на рис. 3.30.

Рисунок 3.30 – Эквивалентная схема для ёмкостного фильтра

На этом рисунке 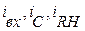– переменные составляющие тока. Передача постоянной составляющей тока I₀ (и напряжения) выполняется с , так как потерь по постоянному току в фильтре нет. Коэффициент сглаживания фильтра равен: (3.36)

Поскольку (3.37)

(3.38)

Подстановка (3.37) и (3.38) в (3.36) даёт

. (3.39)

Очевидно, что с увеличением тока нагрузки (уменьшением R_H) коэффициент сглаживания уменьшается. Поэтому ёмкостные фильтры целесообразны при малых токах и высокоомных нагрузках.

Для получения больших коэффициентов сглаживания используют каскадное включение фильтров, как показано на рис.3.31

Рисунок 3.31 – Каскадное включение фильтров

Общий коэффициент сглаживания равен

(3.40)

Выразим его через коэффициенты сглаживания отдельных каскадов, учитывая, что

(3.41)

Подстановка (3.41) в (3.40) даёт

. (3.42)

Видно, что при каскадном соединении коэффициенты сглаживания отдельных звеньев перемножаются, результирующая масса и объём становятся меньше, чем у однозвенного фильтра. Однако возрастает количество собственных резонансных частот, что ухудшает устойчивость всей системы. По этой причине количество звеньев в реальных схемах не превышает 2 (редко 3).