Схемы выпрямления

Простейший выпрямитель обычно содержит: трансформатор, вентиль и нагрузку (рис. 3.15).

Рисунок 3.15 – Простейший выпрямитель

Рисунок 3.16 – Эпюры токов и напряжений простейшего выпрямителя

Это, так называемая, однофазная однотактная схема выпрямления Выпрямленное напряжение (U_d) содержит постоянную составляющую (U₀) и бесконечный ряд гармонических составляющих, первая гармоника которых имеет частоту равную f_сети. За период сети ток i₂ не меняет своего направления, поэтому имеет место постоянное подмагничивание сердечника трансформатора. Ток в первичной обмотке равен сумме тока холостого хода (i_xx) и тока нагрузки, пересчитанного в первичную цепь (i₂^’), который не имеет постоянной составляющей. Форма тока в первичной обмотке (i₁) далека от гармоники, хотя нагрузка активная. В общем случае трансформатор имеет m₁ первичных обмоток (фаз сети) и р фаз во вторичной цепи – число фаз выпрямления, которое называют пульсностью. Обычно m₁ p. Пульсность схемы определяется произведением

, (3.7)

где k – число вторичных обмоток трансформатора

q – число импульсов тока за период в одной обмотке.

Поэтому схема рис. 3.15 называется однофазная и однотактная (р=1*1=1).

Рассмотрим схему с пульсностью р =2, которая приведена на рис.3.17. Здесь две вторичных обмотки и через каждую из них за период сети протекает один импульс тока i₂^’ и i₂^’’. Причём, через нагрузку они протекают в одном направлении, а через вторичные обмотки – в разных направлениях и не создают постоянного подмагничивания сердечника трансформатора. Тогда получаем , то есть схема двухфазная однотактная.

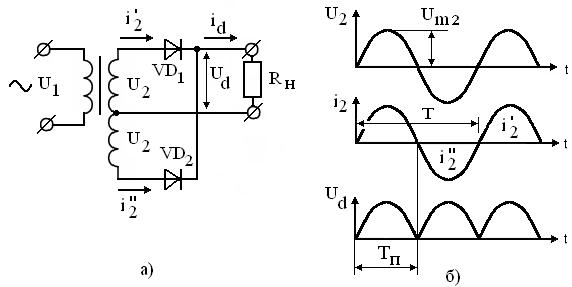
Рисунок 3.17–Двухфазный однотактный выпрямитель (схема со средней точкой)

Частота первой гармоники пульсаций вдвое выше частоты сети (Т_П=Т/2) и находится через пульсность

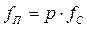(3.8)

Рассмотрим однофазный мост. Его схема приведена на рис.3.18. Эпюры напряжений соответствуют рис.3.17б. Учитывая, что здесь одна вторичная обмотка, находим пульсность , то есть схема однофазная двухтактная. Частота первой гармоники пульсаций вдвое выше частоты сети (как и в предыдущей схеме). Однако они различаются обратными напряжениями на вентилях – в схеме рис. 3.17 , а в схеме 3.18 . Кроме того, в схеме рис. 3.17 в цепи тока находится только один диод, а в схеме 3.18 – два диода. Поэтому, в низковольтных выпрямителях предпочтительна схема со средней точкой.

Рисунок 3.18 – Однофазный двухтактный выпрямитель (однофазный

мост)

Рассмотрим трёхфазный выпрямитель.

Трёхфазная однотактная схема выпрямления приведена на рис. 3.19. Эту схему называют также трёхфазной с нулевым выводом или трёхфазной со средней точкой.

Она состоит из трёхфазного трансформатора и трёх вентилей VD1, VD2 и VD3. Нагрузка включается между точкой соединения вентилей и общей точкой вторичных обмоток трансформатора. На рис. 3.20 представлены эпюры токов и напряжений в различных точках схемы.

Рисунок 3.19 – Трёхфазная схема с нулевым выводом

Рисунок 3.20 – Эпюры токов и напряжений для схемы рис.3.19

Трёхфазная двухтактная схема выпрямления (трёхфазный мост или схема Ларионова) приведена на рис. 3.21.

Рисунок 3.21 – Трёхфазная двухтактная схема выпрямления

На рис. 3.22 представлены эпюры токов и напряжений в различных точках схемы. Напряжение на нагрузке является суммой выходных напряжений двух трёхфазных, однотактных выпрямителей, каждый из которых использует свою полуволну фазного напряжения U_d=U_d1+U_d2.

Рисунок 3.22 – Эпюры токов и напряжений для схемы рис.3.21

Учитывая, что здесь три вторичных обмотки, находим пульсность . Частота первой гармоники пульсаций .

Существуют и другие схемы выпрямления с пульсностью 9, 12, 18, 24, 48, 96 и т.д. Это специальные схемы, так называемые, многопульсные выпрямители. Для примера, на рис.3.23 приведена схема 12-пульсного выпрямителя. Она представляет собой последовательное соединение двух трёхфазных мостовых схем. Здесь используется трансформатор с тремя обмотками. Вторичных обмоток две: одна соединяется в звезду, а вторая в треугольник, поэтому вторичные напряжения оказываются сдвинутыми по фазе на угол 30^о. Каждая из вторичных обмоток подключена к мосту, а так как мосты включены последовательно, то сумма напряжений содержит 12-кратные пульсации.

Рисунок 3.23 – 12- пульсная схема выпрямления

Получим количественные соотношения для различных схем выпрямления.

3.4 Расчётные соотношения для неуправляемых выпрямителей

Неуправляемый выпрямитель характеризуется рядом показателей к которым относятся, выходное напряжение – U ₀, коэффициент пульсаций – К_П, частота первой гармоники пульсаций – f_п, коэффициент выпрямления и др. Найдём эти показатели для разных схем выпрямления.

Простейший выпрямитель (рис. 3.15, пульсность р=1). Форма выходного напряжения приведена на рис. 3.24а.

Мгновенное напряжение U_d на интервале подчиняется закону косинуса (повторяет напряжение U₂)

(3.9)

Среднее значение выходного напряжения равно

. (3.10)

Рисунок 3.24 – Выходное напряжение при разной пульсности

Отношение

(3.11)

называют коэффициентом выпрямления. Он показывает степень использования трансформатора. Для нашего случая

(3.12)

т.е. довольно низкая величина.

Найдём теперь коэффициент пульсаций по первой гармонике.

Если грубо принять напряжение U_d гармоническим и считать, что его амплитуда , то . Поэтому, такие схемы без сглаживающих фильтров не используют.

Обратное напряжение на вентиле равно U_обр = U_m2.

Для двухфазной однотактной схемы (рис. 3.17 пульсность р=2).

Среднее значение (постоянная составляющая) выходного напряжения (рис.3.24 б) равно

(3.13)

Коэффициент выпрямления равен

(3.14)

Если грубо принять напряжение U_d гармоническим и считать, что , то . Если же периодическую кривую напряжения Ud разложить в ряд Фурье и выделить первую гармонику, то получим К_П = 0,667. Это соответствует аналитическому выражению

, (3.15)

которое справедливо при . Частота первой гармоники пульсаций кратна частоте сети

Приведённые соотношения действительны и для мостовой схемы (рис.3.18), поскольку их пульсности одинаковы (р=2). Различными в этих схемах будут обратные напряжения на вентилях, которые соответственно равны:

для р = 2*1 = 2 (3.16)

для р = 1*2 = 2 (мостовая схема).

Для трёхфазной однотактной схемы (рис. 3.19 пульсность р=3). Форма выходного напряжения приведена на рис. 3.24 в.

Среднее значение выходного напряжения (рис.3.24в) равно

(3.17)

Получилась универсальная формула, справедливая при

(3.18)

Если р =2, то

Если р =3, то

Коэффициент выпрямления равен

(3.19)

Что существенно выше, чем в предыдущих схемах.

Если считать, что пульсации гармонические и их двойная амплитуда

, откуда

тогда

При точном разложении напряжения U_d на гармоники, согласно выражению (3.15) получаем К_П = 0,25.

Обратное напряжение на вентиле равно линейному:

(3.20)

Для трёхфазной двухтактной схемы (рис. 3.21 пульсность р=6) получаем:

(3.21)

В схеме выпрямления вторичные обмотки включены звездой, поэтому U_m2 следует умножить на .

(3.22)

К_П = 0,057

При включении вторичных обмоток треугольником множитель не нужен и . Видно, что с ростом пульсности, растёт коэффициент использования трансформатора и уменьшается коэффициент пульсаций. Поэтому схема Ларионова получила широкое распространение в преобразовательной технике.

В 12- пульсной схеме выпрямления, которая приведена на рис. 3.23 коэффициент пульсаций составляет всего 1,4% и поэтому она может применяться без сглаживающего фильтра.