Конечные автоматы с памятью (последовательностные)

Для таких автоматов характерно наличие вектора внутренних состояний z=(z₁, z₂,…, z_m).

В таких автоматах каждая логическая функция зависит от входных функций x и функций внутреннего состояния z.

Рис. 10. Конечный автомат с памятью

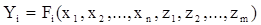
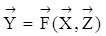. (8)

Для автоматов с памятью характерно, что они функционируют во времени, и в момент времени t₀ должно быть задано начальное состояние z₀. В момент времени t₀ 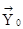определяется выражением (8). В момент времени t₁=t₀+t входной вектор может поменяться, в свою очередь может поменяться вектор состояний Y.

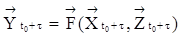, (9)

где t – такт логического конечного автомата. Считается, что t много больше времени расчета на ЭВМ.

Пример.

Та же самая экспертная система определения профессиональной пригодности, но с условием, что значение о профессиональной пригодности зависит от ранее полученных ответов. Такие экспертные системы называют самообучающимися, т. к. сразу правильного ответа не дают. Частным случаем конечного автомата с памятью является автомат с обратной связью по выходу. Для него вектор внутренних состояний в момент времени t+t равен вектору выходных сообщений в момент времени t. Пример конечного автомата с памятью и обратной связью по выходу приведен на рис. 11.

Рис. 11. Конечный автомат с памятью и обратной связью по выходу

Экспертная система является примером конечного автомата с памятью с обратной связью по выходу. Программная модель такого автомата базируется на программной модели автомата без памяти, однако, помимо уже накопленного опыта добавляется процедура tact, а также начальные значения входных и выходных переменных.

Const

N=…; k=…;

Type

Vector x = array [1..n] of boolean;

Vector y = array [1..k] of boolean;

Var

X: vector X;

Ypred, Y: vector Y;

Procedure tact (v: vector X; var Ypred, Y: vector Y);

Var

I: integer;

Begin

Y[1]:=y₁(…);

Y[2]:=y₂(…);

Y[3]:=y₃(…);

Y[k]:=y_k(…);

For i:=1 to k do

Ypred[i]:= Y[i];

End;

End.

Состояние конечного автомата называется установившимся, если с течением времени при постоянном значении входного вектора Х, вектор Y принимает постоянное значение. В этом случае процесс обучения конечного автомата заканчивается, и результаты его работы могут быть использованы. Однако существуют автоматы, состояние которых не устанавливается с течением времени. Такие автоматы используются только в схемотехнике. Примером такого автомата является автомат триггерного типа. Логическая схема триггера приведена на рис. 12.

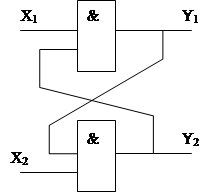Рис. 12. Автомат триггерного типа

Другим частным случаем является автономный конечный автомат, для которого вектор входных воздействий 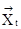отсутствует. Для него вектор выходных состояний является функцией от вектора внутренних состояний 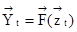. Для него 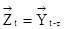(с обратной связью по выходу), тогда . Такие конечные автоматы называют также генераторами высказываний или генераторами логической последовательности. Они могут использоваться для отладки и моделирования некоторых ситуаций.

Контрольные вопросы

1. Что такое логический конечный автомат?

2. Представьте в виде рисунка логический конечный автомат.

3. Что такое такт конечного логического автомата?

4. Приведите пример конечного автомата без памяти.

5. Приведите пример конечного автомата с памятью.

6. Приведите пример конечного автомата с обратной связью по выходу.