Процедура получения оценок максимального правдоподобия

Целевая функция типа (2.109) называется функцией максимального правдоподобия. Несложно заметить, что оптимальные значения оценок параметров a ₀^*, a ₁^*,..., a_n ^*и дисперсии фактической ошибки s _e ², соответствующие ее максимуму, должны обеспечивать и максимум ее логарифма. Иными словами, при определении значений этих оценок можно решать задачу максимизации 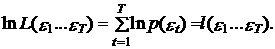В таком случае в условиях независимости разновременных ошибок e_t и e_t–i

Не принимая во внимание первое постоянное слагаемое в правой части выражения (2.111), заметим, что оптимальные значения a ₀^*, a ₁^*,..., a_n ^* и s _e ² в этом случае могут быть найдены путем решения следующей системы из п +2-х дифференциальных уравнений в частных производных по этим параметрам:

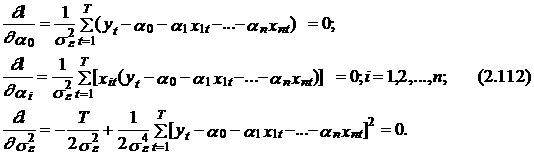
Для получения более компактной векторно-матричной формы записи решения системы (2.112) представим линейную эконометрическую модель в векторно-матричной форме:

у = Х × a + e, (2.113)

где вектор у и матрица Х определены выражением (2.110) и вектор ошибки e имеет такой же вид, как и вектор у; вектор параметров a =(a ₀, a ₁,..., a_n)¢.

На основании (2.113) вектор ошибки можно представить в следующем виде:

e = у – Х × a, (2.114)

и последнее слагаемое в выражении (2.111) записать как скалярное произведение вектора ошибки строки на ее столбец. С учетом этого выражение (2.111) приобретает следующий вид:

(у – Х × a)¢×(у – Х × a). (2.115)

Дифференцируя выражение (2.115) по неизвестному вектору параметров a и по неизвестной дисперсии ошибки s_e ², получим следующую векторно-матричную форму записи системы (2.112):

¶ l /¶ a = (– Х ¢ × у + Х ¢ × Х × a)=0;

¶ l /¶ s_e ²= (у – Х × a)¢×(у – Х × a)=0. ^(2.116)

Поскольку s_e ²¹0, из первого уравнения системы (2.116) непосредственно получаем вектор оценок ММП коэффициентов линейной эконометрической модели в следующем виде:

a ^*= a =(Х ¢ Х)^–1× Х ¢× у, (2.117)

а из второго – оценку ММП дисперсии ошибки эконометрической модели:

s _е ² = (у – Х × a)¢×(у – Х × a)=

Заметим, что выражение (2.117) ничем не отличается от своего аналога (2.8), полученного с использованием МНК, а оценка дисперсии ошибки модели, полученная на основании выражения (2.118), является смещенной. Вследствие этого на практике используют несмещенную оценку дисперсии, определяемую следующим образом^*:

Известно, что оценки параметров, полученные с использованием ММП, обладают свойством состоятельности^**:

plim(a)= a,

plim(s_e ²)= s_e ²,

имеют асимптотически нормальное распределение и асимптотически эффективны,

a a a

N, I ^–1 ,

s_e ² s_e ² s_e ²

где – символ асимптотического приближения, в данном случае закона распределения вектора-столбца оценок к закону нормального распределения с параметрами – их математическими ожиданиями (a, s_e ²)¢ и ковариационной матрицей I ^–1(a, s_e ²)¢, обратной так называемой информационной матрице этих параметров.

Заметим, что состоятельность оценок ММП следует из совпадения с оценками МНК, которые, как было показано в разделе 2.1.2, являются состоятельными. Асимптотические свойства оценок ММП также определяются стремлением к нулю их дисперсий с ростом числа измерений, что следует из свойств элементов матрицы I ^–1(a, s_e ²).

Напомним, что I (z) – информационная матрица случайного вектора z, определяется следующим образом:

I (z)= – M [¶² l /¶ z ¶ z ¢], (2.120)

где матрица ¶² l /¶ z ¶ z ¢ имеет следующий вид:

¶² l /¶ z ¶ z ¢ =

и в нашем случае k = n +2 и z ₁= a ₀,..., z_{k– 1}= a_n, z_k = s_e ².

Выполнив двойное дифференцирование выражения (2.116) по вектору a и s_e ², получим

¶² l /¶ a ¶ a ¢=– Х ¢ Х / s_e ² ; – M [¶² l /¶ a ¶ a ¢]=– Х ¢ Х / s_e ² ;

¶² l /¶ a ¶ s_e ²=– Х ¢ e / s_e ⁴; – M [¶² l /¶ a ¶ s_e ²]=0.

Последнее равенство выполняется в силу предполагаемой независимости значений факторов х_it (столбцов матрицы X) и ошибки e, являющейся “белым шумом”.

¶² l /(¶ s_e ²)²= T /2 s_e ⁴– e ¢ e / s_e ⁶; – M [¶² l /(¶ s_e ²)²]= T /2 s_e ⁴, поскольку M [ e ¢ e ]= T × s_e ².

Таким образом, информационная матрица вектора (a, s_e ²)¢ определяется следующим выражением:

^I

а ковариационная матрица этого вектора имеет следующий вид:

^{I –1}

где 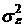(Х ¢ Х)^–1 – представляет собой ковариационную матрицу вектора оценок параметров a, а – дисперсию дисперсии модели s_e ².

Из выражения (2.123) вытекает, что ковариационная матрица вектора оценок параметров линейной эконометрической модели (1.2) имеет следующий вид:

Cov (a)= s_e ² ×(Х ¢× Х)^–1= W _a @ s_e ² ×(Х ¢× Х)^–1. (2.124)

В выражении (2.124) учтено, что на практике оценка дисперсии истинной ошибки s_e ² может быть заменена ее оценкой s_e ², определенной согласно выражению (2.119) с использованием “фактических” значений ошибки e_t.

Из выражения (2.124) непосредственно следует, что дисперсии оценок параметров линейных эконометрических моделей , определенных по ММП, являются диагональными элементами матрицы s_e ²×(Х ¢× Х)^–1. Напомним, что среднеквадратические ошибки этих параметров ( ) используются при определении значимости факторов модели (см. выражение (1.25)).

Таким образом, из результатов раздела 2.5 вытекает, что при предположении о нормальном законе распределения ошибки эконометрической модели и ее свойствах, определенных выражениями (2.20)–(2.24), оценки ее коэффициентов, полученные с использованием методов максимального правдоподобия и наименьших квадратов совпадают. Аналогичное совпадение отмечается и у ковариационных матриц этих оценок. Несложно показать, что в этих условиях у МНК и ММП совпадают также оценки параметров эконометрических моделей, полученные при ограничениях на их значения (см. выражение (2.91)).

Если же ошибки модели распределены по другому закону (например, Гаусса с тяжелыми хвостами, Стьюдента и т. п.), то вообще говоря, выражения для оценки коэффициентов, полученные на основе ММП, будут отличаться от их аналогов, полученных с использованием МНК.

Вопросы к главе II

1. Каковы предпосылки «классического» метода наименьших квадратов (МНК)?

2. В чем суть МНК?

3. Приведите формулы расчета оценок коэффициентов линейной модели по МНК?

4. Какими свойствами обладают МНК-оценки классической линейной эконометрической модели?

5. Перечислите свойства фактической ошибки эконометрической модели.

6. Каким образом тестируется условие постоянства дисперсии ошибки модели?

7. Каким образом проверяется наличие автокорреляции ошибок модели?

8. Как оценивается дисперсия истинной ошибки модели?

9. Каковы последствия мультиколинераности факторов?

10. Как проверяется обратимость матрицы Х ¢ Х?

11. Каковы последствия неправильного выбора состава независимых переменных модели?

12. Каковы особенности оценивания параметров с учетом наложенных ограничений?

13. Перечислите предпосылки метода максимального правдоподобия (ММП)?

14. Опишите процедуру получения оценок параметров эконометрической модели с помощью ММП.

15. Какими свойствами обладают ММП-оценки параметров?

16. Каким образом оценивается дисперсия истинной ошибки модели?