Засобами MS Excel

Приклад розрахунку аналітичних показників інтенсивності динаміки за даними, наведеними у табл. 10.1. Вихідний ряд динаміки розміщено в комірках (В3:B8) (Рис.10.4). Для розрахунку ланцюгових, базисних і середніх показників динаміки обсягу реалізованої продукції використаємо вищенаведені формули у п.10.2 та п. 10.3.

Рис. 10.4. Вихідні дані щодо розрахунку аналітичних показників інтенсивності динаміки

Отримаємо такі результати розрахунків аналітичних показників інтенсивності динаміки обсягу реалізованої продукції за шість років (рис. 10.5):

Рис. 10.5. Результати розрахунку аналітичних показників інтенсивності динаміки

Отже, середньорічний обсяг реалізованої продукції становить 26,8 тис. грн. Протягом 2005-2010 рр. обсяг реалізації зріс на 13 тис. грн. або на 65 %. У середньому за рік реалізована продукція зростала на 2,6 тис. грн. або на 10,5%.

Для наочної уяви про динаміку реалізованої продукції подаємо ряд динаміки у вигляді лінійного графіка та стовпчикової діаграми. Для побудови лінійного графіка використовують «Мастер диаграмм – Тип «График» – Вид1»:

Для того, щоб оформити графік належним чином, доцільно натиснути «Далее» – «Параметры диаграммы» – «Заголовки» та у відповідні поля ввести назву графіка, назви показників:

Аналогічно будується стовпчикова діаграма, тільки обирається тип графіка «Гистограмма».

З використанням Мастера диаграмм отримуємо лінійний графік і стовпчикову діаграму (рис. 10.6, 10.7):

Рис. 10.6. Графік динаміки обсягу продукції за 2005-2010 рр.

Рис. 10.7. Діаграма динаміки обсягу продукції за 2005-2010 рр.

Приклад виявлення тенденцій розвитку явищ методом рухомої (козної) середньої. Для реалізації методу рухомої (козної) середньої можна скористатися пакетом «Анализ данных» – Инструмент анализа – «Скользящее среднее»:

Введемо у поле «Входной интервал» вихідний ряд динаміки (рис. 10.8), у полі «Интервал» задамо інтервал вирівнювання 3, зробимо відмітку для побудови графіку.

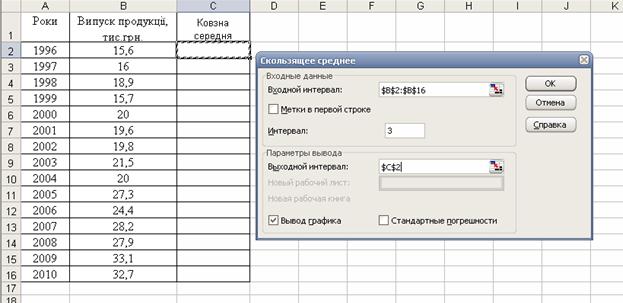
Рис. 10.8. Вихідні дані щодо реалізації методу рухомої (козної) середньої

Головним недоліком даного методу є те, що вирівняний ряд стає коротшим від вихідного за рахунок втрати рівнів на початку та у кінці ряду динаміки. Після виконання програми отримаємо такі результати (рис. 10.9):

Рис. 10.9. Результати реалізації методу рухомої (козної) середньої

Приклад виявлення тенденцій розвитку явищ методом аналітичного вирівнювання. Вихідний ряд динаміки розміщено у комірках А1:В16.

Для одержання передбачених в Excel п'яти видів рівняння тренду використаємо «Мастер диаграмм» – Тип – График:

Після того, як побудовано лінійний графік, можна одержати п'ять рівнянь тренду: лінійне, логарифмічне, поліноміальне, степеневе та експоненційне. Для вибору найкращого рівняння тренду необхідно побудувати усі п'ять типів графіків, вивести на поле кожного графіка відповідне рівняння та величину помилки апроксимації R ². Для цього необхідно поставити курсор на лінію графіка та натиснути праву кнопку миші, у вікні, яке з'явиться, обрати команду «Добавить линию тренда», вибрати потрібний тип рівняння:

Рис. 10.10. Вибір рівняння тренду

Потім необхідно задати у підменю «Параметры» дві команди – «Показывать уравнение на диаграмме» та «Поместить на диаграмму величину достоверности аппроксимации»:

Наприклад, результат підбору лінійного та поліноміального (поліном 2-го степеня) рівнянь тренду за даними, наведеними у комірках А2:В16 (рис. 10.11, 10.12).

Рис. 10.11. Результат підбору лінійного рівняння тренду

Рис. 10.12. Результат підбору поліноміального (поліном 2-го степеня) рівняння тренду

За критерієм R ²поліном забезпечує вищий рівень апроксимації вихідного ряду динаміки, тому ця модель має перевагу порівняно з лінійною. Аналогічно можна порівняти результати розрахунків за іншими типами рівняння, використовуючи запропонований їх перелік:

Приклад розрахунку індексів сезонності за даними табл. 10.6, які занесені у комірки В3:Е6:

Для вироблення гіпотези про наявність та характер сезонних коливань побудуємо графік з використанням «Мастера диаграмм», але спочатку сформуємо єдиний ряд динаміки за чотири роки (комірки G2:G17) (рис. 10.13):

Рис. 10.13. Виявлення наявності сезонних коливань графічним методом

Одержаний графік дає підстави для висновку, що значення показника не мають тенденції, тобто коливаються навколо середнього рівня, отже для оцінювання сезонних коливань скористаємося формулою:

Для розрахунку індексів сезонності обчислимо середні значення за кожний квартал, а також загальне середнє значення, після чого знайдемо відношення:

Рис. 10.14. Результати розрахунку індексів сезонності

Отже, за результатами розрахунків одержуємо такі індекси сезонності доходів від надання послуг міського телефонного зв’язку: І квартал – 97,65 %; ІІ квартал – 95,41 %; ІІІ квартал – 98,77 %; IV квартал – 108,18 %.

Можна зробити висновок про те, що сезонні коливання є досить сильними. Для візуалізації сезонних коливань використовують графік сезонної хвили, у якому по осі ординат показують час (період), а по осі ординат – індекси сезонності. Побудований за результатами розрахунків графік сезонної хвили підтверджує вищезазначені висновки (рис.10.15):

Рис. 10.15. Сезонна хвиля доходів від надання послуг міського телефонного зв’язку за 2006–2009 рр.

Запитання і завдання для самоконтролю

10.1. Поняття і складові елементи ряду динаміки.

10.2. Види рядів динаміки.

10.3. Порівнянність рівнів у рядах динаміки.

10.4. Абсолютні та відносні характеристики інтенсивності динаміки, способи обчислення та взаємозв’язок.

10.5. Оцінка прискорення (уповільнення) розвитку.

10.6. Порівняльний аналіз динамічних рядів.

10.7. Коефіцієнт випередження.

10.8. Середні рівні і показники рядів динаміки, способи їх обчислення.

10.9. Тенденції розвитку в рядах динаміки соціально-економічних явищ.

10.10. Методи виявлення основної тенденції розвитку.

10.11. Сезонні коливання, методи їх вимірювання.

Література [3; 5; 7; 8; 15–24; 26].