Структурні середні

Для статистичної характеристики варіаційних рядів обчислюють структурні (порядкові) середні, до яких відносять моду і медіану.

Для розглянутих вище середніх необхідно використовувати всі наявні значення ознаки. Мода і медіана визначаються лише структурою розподілу. Тому їх іменують структурними позиційними середніми.

Модою називається величина ознаки (варіанта), яка найчастіше зустрічається в даній сукупності.

Знаходження моди в дискретному варіаційному ряду не є складною. Розглянемо приклад.

Таблиця 5.5 – Розподіл студентів за їх ростом

Ріст студентів, см

Число студентів, чол.

Очевидно, в цьому прикладі модою буде студент, який має ріст 180 см, тому що цьому значенню ознаки (варіанті) відповідає найбільше число студентів (55 чол.).

Медіана – це варіанта, яка займає середнє положення в упорядкованому варіаційному ряду і поділяє його на дві рівні частини.

Щоб знайти медіану в дискретному варіаційному ряду, потрібно спочатку розташувати всі варіанти в зростаючому або спадаючому порядку. Потім визначити номер медіани, який вкаже на її розташування в упорядкованому ряді за формулою:

де М_е – медіана; п – число варіант.

Розглянемо приклад.

Таблиця 5.6 – Розподіл дев’яти деталей за їх масою

Номер деталі
Маса, г	2,6	3,4	3,3	2,7	3,0	2,9	2,8	3,1	3,2

Перегрупуємо деталі за їх масою в зростаючому порядку.

Таблиця 5.7 – Упорядкований розподіл дев’яти деталей за їх масою

Номер деталі
Маса, г	2,6	2,7	2,8	2,9	3,0	3,1	3,2	3,3	3,4

Визначаємо номер медіани:

Тобто під п’ятим номером від початку або від кінця ряду маса деталі буде медіаною. М_е = 3,0 г.

Коли варіаційний ряд має парну кількість членів, тоді медіана буде розраховуватись як півсума двох варіантів, які займають середнє положення в упорядкованому ряду. Припустимо, що є ще десята деталь з масою 3,5 г. Номер медіани буде дорівнювати У даному випадку медіана буде розташована між п’ятим і шостим порядковим номером деталей.

Моду і медіану із інтервальних рядів визначають розрахунковим шляхом за наступними формулами:

де М_о – мода;

– нижня межа модального інтервалу;

h – розмір модального інтервалу;

– модальна частота;

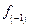– передмодальна частота;

– післямодальна частота.

де М_е – медіана;

– нижня межа медіанного інтервалу;

h – розмір медіанного інтервалу;

– сума частот;

– сума нагромаджених частот до медіанного інтервалу;

–частота медіанного інтервалу.

Покажемо обчислення моди і медіани для інтервального варіаційного ряду на прикладі.

Таблиця 5.8 – Розподіл 500 працівників за заробітною платою

Заробітна плата, грн.	Число працівників, чол.	Накопичені частоти
1500–1600 1600–1700 1700–1800 1800–1900 1900–2000 2000–2100 2100–2200 2200–2300 2300–2400
Разом:		×

У даному прикладі мода знаходиться в інтервалі від 1900 до 2000 грн., тому, що йому відповідає найбільша частота (130 чол.). Цей інтервал називається модальним.

грн.

Цей показник означає, що найбільше працівників було із заробітною платою 1954,3 грн.

Щоб визначити медіану інтервального варіаційного ряду спочатку, за допомогою нагромаджених частот, потрібно знайти інтервал, що містить медіану. Медіанному інтервалу відповідає перша з нагромаджених частот, яка перевищує півсуму частот усього обсягу сукупності Отже, медіана знаходиться в інтервалі від 1900 до 2000 грн.

грн.

Це означає, що половинна працівників отримує заробітну плату меншу 1953,1 грн., а друга половина – більшу.

Мода, медіана відносяться до так званих порядкових статистик, під якими розуміють варіанти, які займають певне порядкове місце в упорядкованому варіаційному ряду.

Їх використання в статистичному аналізі варіаційних рядів дозволяє більш глибоко дослідити і детальніше охарактеризувати сукупність, яка вивчається.