Задание № 4. 4.1.Записать уравнения касательной и нормали к кривой в точке при х0 = 2

4.1. Записать уравнения касательной и нормали к кривой в точке при х ₀ = 2. Сделать чертеж.

4.2. Составить уравнения касательной и нормали к астроиде в точке . Сделать чертеж.

4.3. Составить уравнения касательной и нормали к астроиде в точке при . Сделать чертеж.

4.4. Найти уравнения касательной и нормали к гиперболе в точке . Сделать чертеж.

4.5. Составить уравнения касательной и нормали к эллипсу в точке . Сделать чертеж.

4.6. Составить уравнения касательной и нормали к кривой в точке пересечения ее с параболой у = 2 х ². Сделать чертеж.

4.7. Найти величину угла, под которым пересекаются параболы и (при х < 3). Сделать чертеж.

4.8. Составить уравнения нормали и касательной к кривой x = t ³; у = t ² при t ₀ = –1. Сделать чертеж.

4.9. Найти величину угла между кривыми х ² + у ² = 5 и у ² = 4 х в точке их пересечения при y > 0. Сделать чертеж.

4.10. Найти угол между кривыми в точках их пересечений. Сделать чертеж.

4.11. Составить уравнения касательной и нормали к кривой в точке (х ₀, у ₀), в которой касательная параллельна прямой .

4.12. Составить уравнения касательной прямой к пространственной линии в точке .

4.13. Составить уравнения касательной прямой к пространственной линии (R = const) в точке . Сделать чертеж.

4.14. Составить уравнения касательной и нормали к линии 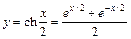в точке при . Сделать чертеж.

4.15. Определить величину угла, который касательная к кривой в точке (0; 0) составляет с осью Ох. Составить уравнения касательной и нормали к этой кривой в точке (0; 0). Сделать чертеж.

4.16. Зависимость пути от времени при прямолинейном движении точки задана уравнением . Найти скорость и ускорение движения при .

4.17. По параболе у = (8 – х) х движется точка (х, у) так, что абсцисса изменяется по закону х = . Найти скорость изменения ординаты в точке М (1, 7).

4.18. При бурении нефтяной скважины глубина проходки изменяется по закону (t – время в часах, s – в метрах). В какой момент времени скорость проходки будет 15 м / ч?

4.19. Тело движется прямолинейно по закону s (t) = . Найти скорость и ускорение движения тела в момент времени .

4.20. Ракета движется прямолинейно по закону , где x – расстояние от поверхности Земли в метрах, t – время в секундах. Определить скорость и ускорение движения ракеты в момент времени сек.

4.21. Определить вектор и численное значение скорости вращательного движения по винтовой линии (R = const) в момент .

4.22. Найти вектор и численное значение ускорения движения по закону 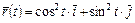в момент .

4.23. Найти вектор и численное значение скорости движения по закону в момент .

4.24. Расстояние между Землей и космическим телом изменяется по закону , где t – время в секундах от момента начала наблюдения, s – расстояние в километрах. Через сколько секунд после начала наблюдения скорость удаления тела от Земли будет 10³ км / с?

4.25. Тело движется прямолинейно в вертикальном направлении по закону h (t) = 7 + 12 t – 9 t ². Определить начальную скорость и ускорение движения тела.

4.26. Тело движется по закону . Найти вектор и численное значение ускорения в момент времени .

4.27. Определить вектор ускорения и его численное значение при вращательном движении по винтовой линии 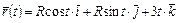(R = const) в момент .

4.28. Тело массой m = 4 кг движется прямолинейно по закону x = t ² + t + 2 (x – расстояние от начала координат в метрах, t – время в секундах). Определить кинетическую энергию тела E = mV ² / 2 в момент .

4.29. Тело движется прямолинейно в вертикальном направлении по закону 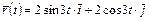. Определить вектор ускорения и его числовые значения при .

4.30. По оси Ox движутся две материальные точки, законы движения которых x = 4 t ² / 3 – 7 t + 16 и x = t ³ + 2 t ² + 5 t – 8. В какой момент времени их скорости окажутся равными?