 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Модель 5
|
|
Имеется две выборки из нормальных генеральных совокупностей  ;
;  .
.
Причём параметры  ,
,  - неизвестны.
- неизвестны.
 ;
;
 .
.
Решение. Найдём точечные оценки дисперсий:
;.
Предположим, что  . Построим статистику
. Построим статистику  . Можно доказать, что при выполнении гипотезы Н0,
. Можно доказать, что при выполнении гипотезы Н0,  - распределение Фишера
- распределение Фишера  , где
, где 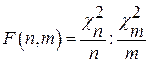 .
.
Возьмем  в качестве критерия проверки гипотезы H0.
в качестве критерия проверки гипотезы H0.
Для гипотезы  область
область  .
.
Если  , то отклоняем Н0 в пользу На; если
, то отклоняем Н0 в пользу На; если  , у нас нет оснований отвергнуть гипотезу Н0. Здесь
, у нас нет оснований отвергнуть гипотезу Н0. Здесь  квантиль распределения Фишера
квантиль распределения Фишера  .
.
Замечание. Для гипотез:

Замечание. Если гипотезу  принимают, то говорят, что различие выборочных дисперсий
принимают, то говорят, что различие выборочных дисперсий  и
и  статистически не значимои оценка общей дисперсии такова:
статистически не значимои оценка общей дисперсии такова:  .
.
Пример 3. Расход сырья на одно изделие случаен. Результаты наблюдений таковы:
| Старая технология | Новая технология | ||||||
| Расход сырья | |||||||
| Число изделий |
Предположив, что расход сырья, как при старой, так и при новой технологии имеет нормальное распределение, выяснить, влияет ли технология на средний расход сырья на одно изделие. Принять  .
.
Решение. Здесь  Найдем выборочные средние:
Найдем выборочные средние:  и
и 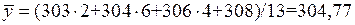 и выборочные дисперсии
и выборочные дисперсии  и
и  .
.
По условию генеральные дисперсии не известны и неизвестно, равны ли они. Поэтому, прежде чем сравнить генеральные средние, проверим гипотезу  , приняв в качестве альтернативной
, приняв в качестве альтернативной  . Согласно
. Согласно  -критерию (см. модель 5), вычислим
-критерию (см. модель 5), вычислим  , а затем найдем по таблице
, а затем найдем по таблице  Так как
Так как  , то
, то  Нулевую гипотезу о равенстве генеральных дисперсий принимаем.
Нулевую гипотезу о равенстве генеральных дисперсий принимаем.
Теперь проверим гипотезу  , приняв в качестве альтернативной
, приняв в качестве альтернативной  . Согласно
. Согласно  - критерию (см. модель 4) вычислим
- критерию (см. модель 4) вычислим
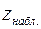 =
=  =3,852.
=3,852.
Далее найдем 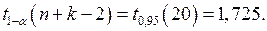 Так как
Так как  , то
, то  Следовательно, принимаем гипотезу
Следовательно, принимаем гипотезу 
 то есть считаем, что применение новой технологии снижает средние затраты сырья на одно изделие.
то есть считаем, что применение новой технологии снижает средние затраты сырья на одно изделие.
Часто при обработке статистической информации можно встретиться с признаками, не поддающимися количественной оценке. Например, невозможно дать количественную оценку математическим способностям студента, качеству продукции и т. д. В этих случаях принято подсчитывать долю или процент генеральной совокупности обладающих тем или иным качественным признаком.
Модель 6. Пусть р – доля элементов генеральной совокупности, обладающих некоторым качественным признаком. Из этой генеральной совокупности извлечена выборка объема n (n≥100) и по ней получена точечная оценка параметра р
 ,
,
где n ‒ объем выборки,  m – число элементов выборки, обладающих исследуемым свойством.
m – число элементов выборки, обладающих исследуемым свойством.
Требуется проверить нулевую гипотезу H0: р=р0
при трех альтернативных:
 : р≠ р0
: р≠ р0
р< р0,
р> р0.
Решение. Проверка нулевой гипотезы  основывается на вычислении выборочной статистики
основывается на вычислении выборочной статистики 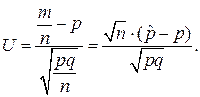
Для решения задачи поступают следующим образом:
 По выборке (2) считают
По выборке (2) считают 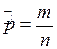 .
.
 По уровню значимости
По уровню значимости 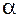 и таблицам находят соответствующий квантиль
и таблицам находят соответствующий квантиль  нормальной случайной величины
нормальной случайной величины 
 ;
;
 Вычисляют
Вычисляют 

 (где q0=1-p0)
(где q0=1-p0)
Для альтернативных гипотез На критическая область G имеет вид: На: 
Тогда, если U набл.  G, то отклоняем гипотезу H0 в пользу альтернативной гипотезы
G, то отклоняем гипотезу H0 в пользу альтернативной гипотезы  Если
Если 
 G, то у нас нет оснований отклонять H0.
G, то у нас нет оснований отклонять H0.
Модель 7. Пусть даны 2 генеральные совокупности, имеющие биномиальный закон распределения (схема Бернулли) с параметрами  и
и  (
(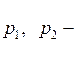 неизвестные доли элементов генеральной совокупности, обладающие заданным качественным признаком).
неизвестные доли элементов генеральной совокупности, обладающие заданным качественным признаком).
Из этих генеральной совокупности извлечены выборки объема n1 и n2 и вычислены 
где mi-количество элементов в i-той выборке, которые обладают качественным признаком, который мы исследуем.
Проверка нулевой гипотезы  основывается на вычислении выборочной статистики
основывается на вычислении выборочной статистики
 , где
, где  ;
;  ;
; 
Для решения задачи поступают следующим образом:
 По выборкам считают
По выборкам считают 
 По уровню значимости
По уровню значимости 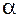 и таблицам находят соответствующий квантиль
и таблицам находят соответствующий квантиль  нормальной случайной величины
нормальной случайной величины 
 ;
;
3. Вычисляют  где
где  ;
;  ;
;
Для альтернативных гипотез критическая область G имеет вид:



Тогда, если 
 G, то отклоняем гипотезу H0 в пользу альтернативной гипотезы
G, то отклоняем гипотезу H0 в пользу альтернативной гипотезы  Если
Если 
 G, то у нас нет оснований отклонять H0.
G, то у нас нет оснований отклонять H0.
Пример 4. Партия изделий принимается в том случае, если вероятность того, что изделие соответствует стандарту  Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли принять партию? Принять уровень значимости a=0,02.
Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли принять партию? Принять уровень значимости a=0,02.
Решение: H0: p= 0,97. Ha: p< 0,97

 ,
, 
Значит справедлива нулевая гипотеза: партия изделий принимается.
Пример 5. Компания А утверждает, что ее зубная паста лучше зубной пасты компании В. Отобраны группы людей nA=400, nB=300 человек, которые чистили зубы зубными пастами компаний А и В. После окончания эксперимента у mA=30, mB=25 человек появились новые признаки кариеса. Проверить гипотезу, что зубная паста фирмы А более эффективна, чем зубная паста фирмы В, если уровень значимости  .
.
Решение: n1=400, m1=30, n2=300, m2=25,  ,
,
H0: p1=p2; 
Ha: p1<p2; 


 . Пасты одинаково эффективны.
. Пасты одинаково эффективны.
16. Критерий 
Пусть основная гипотеза  состоит в том, что функция распределения случайной величины
состоит в том, что функция распределения случайной величины  есть функция
есть функция  , зависящая от
, зависящая от  неизвестных параметров. Процедура применения критерия
неизвестных параметров. Процедура применения критерия  для проверки гипотезы
для проверки гипотезы  состоит из следующих этапов:
состоит из следующих этапов:
 По выборке (2) найдем точечные оценки неизвестных параметров предполагаемого закона распределения
По выборке (2) найдем точечные оценки неизвестных параметров предполагаемого закона распределения  .
.
 Разобьем числовую ось на
Разобьем числовую ось на  промежутков
промежутков 
 ,
, 
 ,
,
 ,
,  ,
,  .
.
Если гипотеза  справедлива, то
справедлива, то  промежутку,
промежутку,  соответствует вероятность
соответствует вероятность  ,
,  .
.
 Пусть из выборки (2)
Пусть из выборки (2)  значений попадает в
значений попадает в  -й промежуток
-й промежуток 
 . Тогда отношение
. Тогда отношение  представляет собой частоту попадания выборочных значений в
представляет собой частоту попадания выборочных значений в  -й интервал. Близость частот
-й интервал. Близость частот  к
к  свидетельствует в пользу гипотезы
свидетельствует в пользу гипотезы  .
.
 Вычисляем выборочное значение статистики
Вычисляем выборочное значение статистики  , которая характеризует согласованность гипотезы
, которая характеризует согласованность гипотезы  с опытными данными.
с опытными данными.
 Принимаем статистическое решение: гипотеза
Принимаем статистическое решение: гипотеза  не противоречит опытным данным на заданном уровне значимости
не противоречит опытным данным на заданном уровне значимости  , если
, если 
 ; если же
; если же 
 , то гипотеза
, то гипотеза  отклоняется. Здесь
отклоняется. Здесь  – квантиль уровня
– квантиль уровня 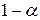 распределения Пирсона с
распределения Пирсона с 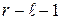 степенями свободы,
степенями свободы,  – число параметров распределения
– число параметров распределения  , которые оцениваются по выборке (2).
, которые оцениваются по выборке (2).
Замечание. Критерий  использует тот факт, что случайная величина
использует тот факт, что случайная величина
 ,
, 
имеет распределение, близкое к нормальному  . Чтобы это утверждение было достаточно точным, необходимо чтобы для всех интервалов выполнялось условие
. Чтобы это утверждение было достаточно точным, необходимо чтобы для всех интервалов выполнялось условие  . Если в некоторых интервалах это условие не выполняется, то их следует объединить с соседними.
. Если в некоторых интервалах это условие не выполняется, то их следует объединить с соседними.
Дата публикования: 2014-10-20; Прочитано: 237 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
